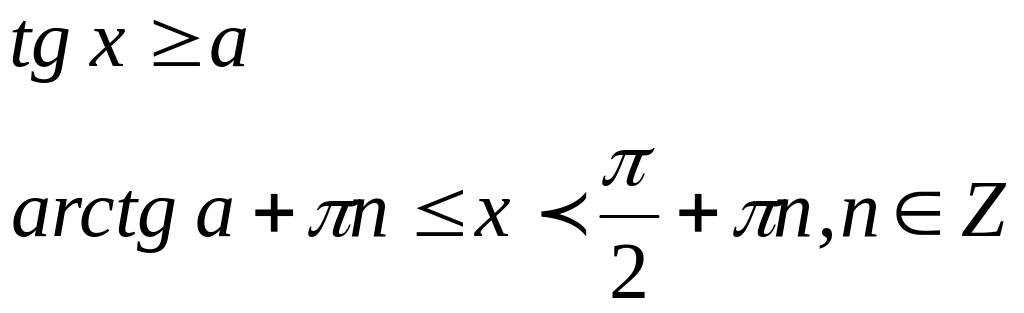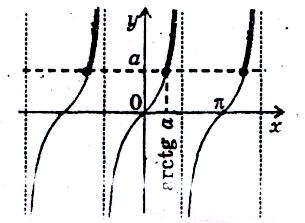
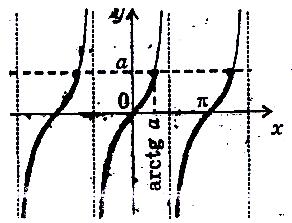
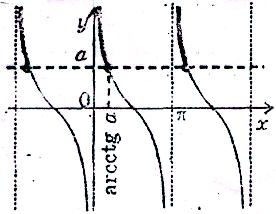
4.4 Найпростіші тригонометричні нерівності

Розділ 5 Похідна та ії застосування

5.1 Границя функції неперервного аргументу. Основні теореми про границі

Нехай дана функція y=f(x). Розглянемо деяку точку х₀, візьмемо досить мале число . Інтервал називається - околом точки х₀.

Якщо для будь-яких х із -околу точки х₀, таких, що х прямує до х₀, значення функції прямують до числа А, то числа А називається границею функції y=f(х) в точці х₀

Основні теореми про границі:

1.

2.

3.

4.

Таблиця границь:

1. 4.

2. 5.

3. 6.

5.2 Неперервність функції в точці та на проміжку. Властивості неперервних функцій

Функція y=f(x) називається неперервною в точці х₀,якщо:

1. Існує значення функції в цій точці

2. Існує границя функції в цій точці

3. Значення функції в т. х₀ дорівнює границі функції в т. х₀ :

Якщо хоча б одна з умов неперервності не виконується, то функція має розрив в т. х₀

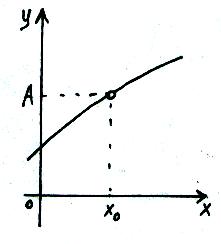
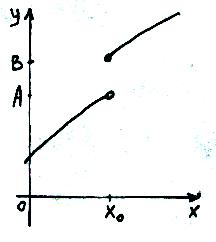
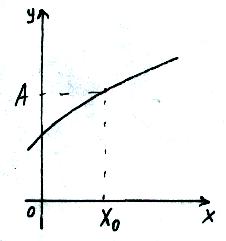
Функція називається неперервною на проміжку, якщо вона неперервна в кожній точці цього проміжку.

Властивості неперервних функцій:

1.Якщо функції f(x) та g(x) неперервні в точці х₀ ,то їх сума, різниця та добуток також неперервні в т. х₀

2. Відношення неперервних в т. х₀ функцій є функція, неперервна в цій точці, якщо значення знаменника в т. х₀ не дорівнює 0.

3. Многочлен є функція, неперервна на всій числовій осі.

5.3 Похідна функції, її фізичний та геометричний змісти

Приростом аргументу називається різниця двох значень аргументу:

Приростом функції називається різниця двох значень функції:

Похідною функції у=f(x) в точці х називається границя (якщо вона існує) відношення приросту функції до приросту аргументу , коли приріст аргументу прямує до нуля, тобто

Функція, яка має скінчену похідну в точці х, називається диференційованою в цій точці.

Знаходження похідної називається диференціюванням функції.

Геометричний зміст похідної

Похідна функції у=f(x) для кожного значення х дорівнює кутовому коефіцієнту дотичної до графіка даної функції у відповідній точці, тобто

де a - кут, який утворює дотична до графіка функції в точці х₀ з додатнім напрямком осі Ох_.

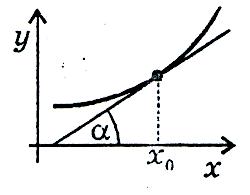
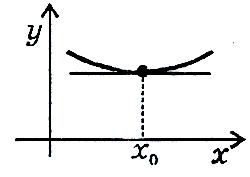
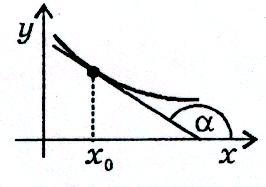
На основі геометричного змісту похідної рівняння дотичної до графіка функції у=f(x) записується таким чином:

Для нормалі, тобто прямої, що проходить через точку дотику М₀ (х₀ ; у₀), перпендикулярно до дотичної , рівняння має вигляд

Фізичний зміст похідної

Під фізичним змістом похідної розуміють швидкість зміни функції в даній точці. Якщо точка рухається вздовж осі х і ії координата змінюється за законом x(t), то миттєва швидкість точки дорівнює похідній від закону руху за часом.

Сила струму в провіднику дорівнює похідній від кількості електрики:

5.4 Основні правила диференціювання.

1. 3.

2. 4.

5.5 Похідна складної функції

Функція, що залежить від функції називається складною функцією:

u(x) – внутрішня функція

f(u(x)) – зовнішня функція

Похідна складної функції дорівнює добутку похідної зовнішньої функції на похідну внутрішньої функції:

5.6 Похідні вищих порядків

Другою похідною функції y=f(x) називається похідна від похідної (позначається ).

Фізичний зміст другої похідної: якщо точка рухається вздовж осі х та її координата змінюється за законом x(t), то прискорення цієї точки дорівнює другій похідній від закону руху: або .

5.7 Зростання і спадання функції. Достатня умова монотонності функції. Дослідження функції на монотонність та екстремум

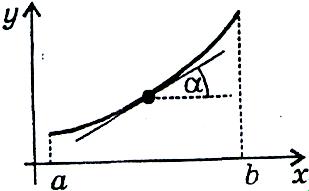
Достатня умова зростання функції: Якщо у кожній точці інтервалу (а;b) , то функція монотонно зростає на цьому інтервалі.

Достатня умова спадання функції: Якщо у кожній точці інтервалу (а;b) , то функція монотонно спадає на цьому інтервалі.

Необхідна і достатня умова сталості функції: Функція стала на інтервалі (а;b) тоді і тільки тоді, коли у кожній точці цього інтервалу.

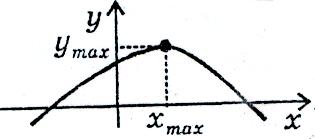
Внутрішня точка х_тах області визначення називається точкою максимуму, якщо для всіх х з деякого околу цієї точки справджується нерівність: .

Значення називається максимумом цієї функції.

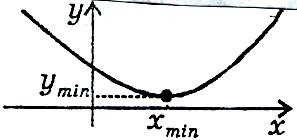
Внутрішня точка х_тіп області визначення називається точкою мінімуму, якщо для всіх х з деякого околу цієї точки справджується нерівність: .

Значення називається мінімумом цієї функції.

Необхідна умова екстремуму: Якщо х₀ – точка екстремуму функції y=f(x),то ця точка є критичною точкою даної функції, тобто у цій точці похідна або дорівнює нулю, або не існує.

Достатня умова екстремуму: Якщо функція y=f(x) неперервна у точці х₀ і похідна змінює знак у цій точці, то х₀ – точка екстремуму функції y=f(x).

Якщо змінює знак з „+” на „-”, то х₀ – точка максимуму.

Якщо змінює знак з „-” на „+”, то х₀ – точка мінімуму.

Примітка: У самій точці х₀ похідна у функції y=f(x)може не існувати.

Приклади екстремумів:

Схема застосування похідної для знаходження інтервалів монотонності та екстремумів:

1. Знайти область визначення функції та інтервали, на яких функція неперервна.

2. Знайти похідну .

3. Знайти критичні точки, тобто точки, в яких похідна функції дорівнює нулю або не існує =0 або - не існує.

4. На кожному інтервалі, на які область визначення розбивається критичними точками, визначити знак похідної і характер зміни функції (за допомогою достатніх умов монотонності).

5. Відносно кожної критичної точки визначити, чи є вона точкою максимуму, мінімуму або не є точкою екстремум.

6. Записати результат дослідження функції: проміжки монотонності і екстремуми.

Приклад: Дослідити функцію на монотонність та екстремум у=2х³-3х²-36х+5

1. D(y): x є R

2. 

3. 

4.

5.

6.