Функція зростає на кожному інтервалі області визначення

y=ctg x

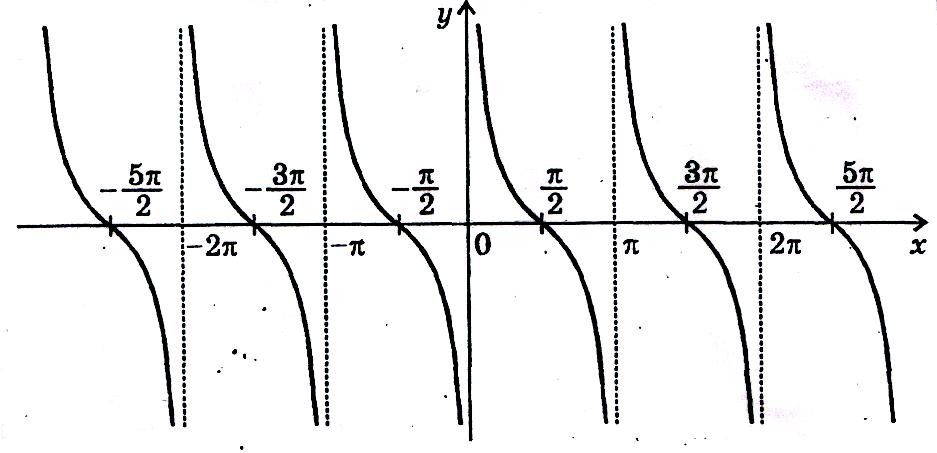
Властивості функції

• Область визначення: об’єднання інтервалів

• Область значення: R

• Парність, непарність: функція непарна

• Період: π

• Нулі: у = 0 при х= πn, n є Z

• Проміжки монотонності:

функція спадає на кожному інтервалі області визначення

3.3 Співвідношення між тригонометричними функціями одного аргументу

sin²x+cos²x=1 tg x∙ctg x=1

Формули зведення

Щоб записати будь-яку формулу зведення, коли , корисно знати такі правила:

1. Якщо кут добудовується відносно вертикального діаметра ( це кути ), то назва даної функції змінюється на кофункцію (синус на косинус, тангенс на котангенс і навпаки); якщо кут добудовується відносно горизонтального діаметра ( це кути, що відповідають числам , ), то назва даної функції не змінюється.

2. Перед утвореною функцією ставиться той знак, який має задана функція, що перетворюється за формулою зведення.

кут функція
sin	cos	sin	-cos	sin
cos	sin	-cos	sin	cos
tg	ctg	tg	ctg	tg
ctg	tg	ctg	tg	ctg

3.4 Формули додавання

sin(x+y)=sin x cos y + cos x sin y cos (x+y)=cos x cos y - sin x sin y

sin(x-y)=sin x cos y - cos x sin y cos (x-y)=cos x cos y + sin x sin y

Формули подвійного аргументу

sin 2x = 2 sin x cos x cos 2x=cos² x – sin² x

Формули пониження степеня

sin²x = ( 1 – cos 2x ) cos² x = ( 1 + cos 2x )

3.5 Формули перетворення суми і різниці тригонометричних функцій на добуток

Формули перетворення добутку на суму

Розділ 4 Тригонометричні рівняння і нерівності

4.1 Обернені тригонометричні функції, їх властивості і графіки

1. Арксінусом числа а називається таке число з відрізку ,сінус якого дорівнює а arcsin а

Функція y=arcsin х, ця функція є оберненою до функції y=sin x, якщо

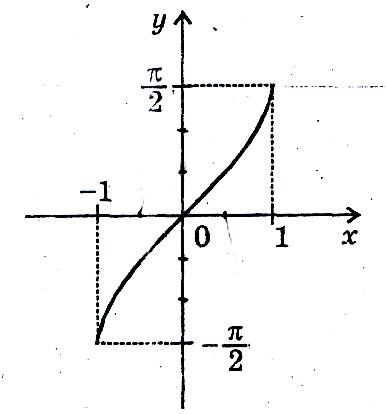
Властивості функцій

• Область визначення: [-1;1]

• Область значення:

• Парність, непарність: функція непарна

• Нулі: у = 0 при х=0

• Проміжки монотонності:

функція зростає на всій області визначення

2. Арккосінусом числа а називається таке число з відрізку , косінус якого дорівнює а arccos а

Функція y=arccos x, ця функція є оберненою до функції y=cos x, якщо