Розділ 2 Показникова і логарифмічна функції

2.1 Логарифм числа. Основна логарифмічна тотожність. Властивості логарифмів

Логарифмом додатного числа b за основою а (а > 0, а ≠ 1) називається такий показник степеня с, до якого треба піднести число а, щоб дістати число b:

log_ab=c a^c=b

Властивості логарифмів:

• Основна логарифмічна тотожність: , b > 0

• log_aа=1 , log_a1=0

• Логарифм добутку дорівнює сумі логарифмів

• Логарифм частки дорівнює різниці логарифмів

• Логарифм степеня дорівнює добутку показника степеня на логарифм основи степеня

• Формула переходу до іншої основи:

де b > 0, с > 0, с≠1; де b > 0, b≠1

Логарифмування – знаходження логарифмів заданих чисел та виразів.

Потенціювання – за логарифмом деякого виразу знайти сам вираз

Десятичним логарифмом називається логарифм за основою 10 і позначається lg.

Натуральним логарифмом називається логарифм за основою числа Ейлера е і позначається ln.

2.2 Показникова і логарифмічна функції, їх графіки і властивості

Показникова функція

Функція у = а^х, де а > 0, а ≠ 1 називається показниковою функцією.

x -1 0 1

y 1 а

а > 1 0 < a < 1

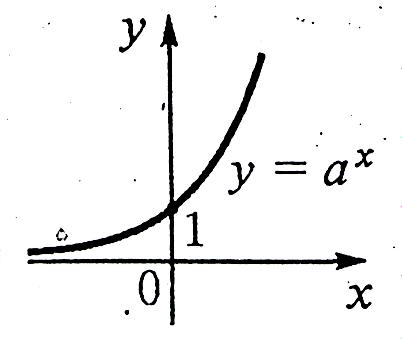
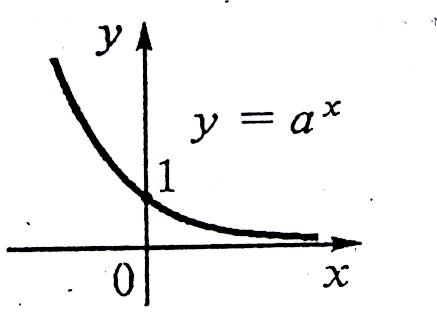
Властивості функцій

• Область визначення: R

• Область значення: (0; )

• Парність, непарність:

функція не є ані парною, ані непарною

• Нулів немає

• Проміжки монотонності:

якщо 0 < а < 1, функція спадає при х є R

якщо а > 1, функція зростає при х є R

• Графік функції проходить через точку (0,1)

Логарифмічна функція

Функція у=log_aх, де а> 0, а≠1 називається логарифмічною функцією

x 1 а

y -1 0 1

а > 1 0 < a < 1

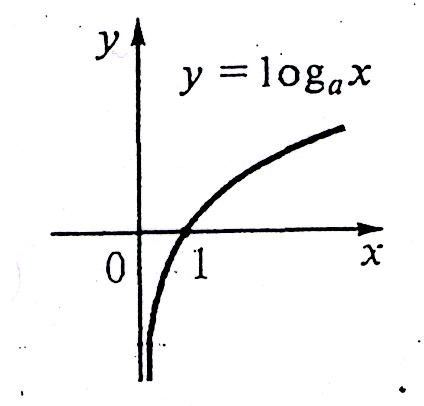
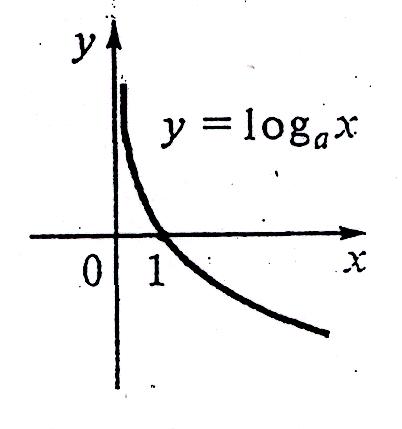
Властивості функцій

• Область визначення: (0; )

• Область значення: R

• Парність, непарність:

функція не є ані парною, ані непарною

• Нулі: у=0 при х=1

• Проміжки монотонності:

якщо 0 < а < 1, функція спадає при х є (0; )

якщо а > 1, функція зростає при х є (0; )

• Графік функції проходить через точку (1,0)

2.3 Показникові рівняння

Рівняння, в якому невідоме міститься в показнику степеня, називається показниковим.

Види показникових рівнянь

1. Спосіб дорівнювання основ.

а ^f(x) = a ^g(x) f(x) =g(x)

а ^f(x) =в; а ^f(x)= ; f(x) =log_aв

2. Перетворення до квадратного рівняння

Аа^2х+Ва^х+С=0 Заміна: а^х=у, тоді а^2х=у²

Ау²+Ву+С=0 Знайдемо у₁ , у₂ Підставимо в заміну а^х=у₁ , а^х=у₂ Знайдемо х₁=log_aу₁ ; х₂=log_aу₂ , якщо у₁ > 0, у₂ > 0.

3. Спосіб групіровки та винесення спільного множника за дужки.

4. Логарифмування обох частин рівняння.

2.4 Показникові нерівності

а ^f(x)> a ^g(x) , де а> 0, а≠1

а > 1	0 < а < 1
а f(x)> a g(x) f(x) > g(x) знак нерівності не змінюється	а f(x)> a g(x) f(x)< g(x) знак нерівності змінюється