Розділ 1 Степенева функція

1. Числові функції. Область визначення та область значень.

Способи задання функції. Графік функції. Властивості функції.

Обернена функція

Функцією y=f(x) називається залежність змінної у від змінної х, при якій кожному значенню х ставиться у відповідність єдине значення у.

х – незалежна змінна (аргумент функції),

у – залежна змінна (значення функції).

Областю визначення функції називається множина всіх х, при яких функція має зміст (позначається D(y))

Областю значення функції називається множина всіх у , які ставляться у відповідність х (позначається E(y))

Графіком функції називається множина точок площини з координатами

(x, f(x))

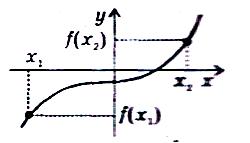
Способи задання функції

• Аналітичний спосіб функція задається за допомогою математичної формули.

• Табличний спосіб функція задається за допомогою таблиці

• Графічний спосіб функція задається за допомогою графіка

• Описовий спосіб функція задається словесним описом.

Властивості функції

1.Монотоність (зростання, спадання)

Функція y=f(x) називається зростаючою на інтервалі (a; b), якщо для будь-яких х₁ і х₂ з цього інтервалу таких, що х₁‹ х₂, справджується нерівність f(х₁) ‹ f(х₂)

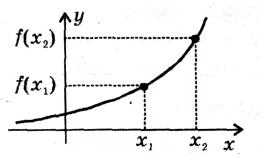
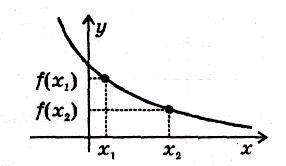
Функція y=f(x) називається спадною на інтервалі (a; b), якщо для будь-яких х₁ і х₂ з цього інтервалу таких, що х₁‹ х₂, справджується нерівність f(х₁) › f(х₂)

2. Парність, непарність

Функція називається парною, якщо для будь-яких х з області визначення функції D(y), ” –х” також належить області визначення D(y) і виконується рівність f(-х)= f(х)

Функція називається непарною, якщо для будь-яких х з області визначення функції D(y), ” –х” також належить області визначення D(y) і виконується рівність f(-х)= -f(х)

Якщо функція не є парною, і не є непарною, то її називають функцією загального вигляду.

Графік парної функції симетричний відносно вісі ординат (рис.1)

Графік непарної функції симетричний відносно початку координат (рис.2)

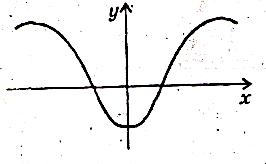
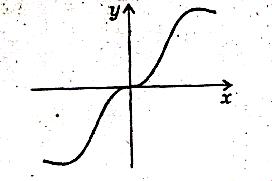
(рис.1) (рис.2)

3. Періодичність

Функція y=f(x) називається періодичною з періодом Т›0, якщо для будь-якого х з області визначення, х+Т та х-Т також належить області визначення і виконується рівність f(x)=f(x+T)=f(x-T)

При цьому будь - яке число вигляду Tּn, де n є N, також є періодом цієї функції.

4. Обернені функції

Поняття оберненої функції може бути застосоване тільки до функцій, що мають таку властивість: кожному значенню у з області значень функції відповідає єдине значення х з області визначення цієї функції.

Функція g називається оберненою для функції f, якщо кожному у з області значень функції f функція g ставить у відповідність таке x з області визначення функції f, що y=f(x). Таким чином, якщо у=f(х),то x=g(y).

Функції f і g є взаємно оберненими.

• Область визначення функції f є областю значень функції g, a область значень функції f є областю визначення функції g.

• Графіки взаємно обернених функцій симетричні один одному відносно прямої у = х. Знаходження формули для функції, оберненої до даної.

За допомогою формули у = f(x) необхідно виразити х через y, a в одержаній формулі х = g(y) замінити x на у, а у на x.

1.2 Побудова графіків функцій за допомогою геометричних перетворень

1. Паралельне перенесення вздовж осі у f(x)→f(x)+b.

Графік функції у=f(x)+b дістається паралельним перенесенням графіка функції у=f(x) вздовж осі у на |b| одиниць: вгору, якщо b › 0, і вниз якщо b ‹ 0

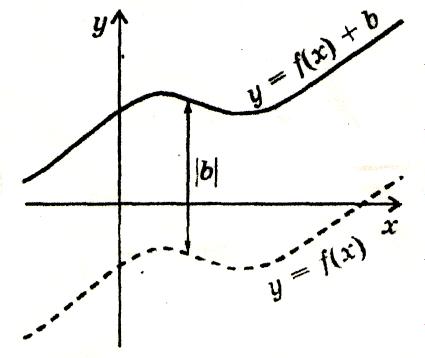
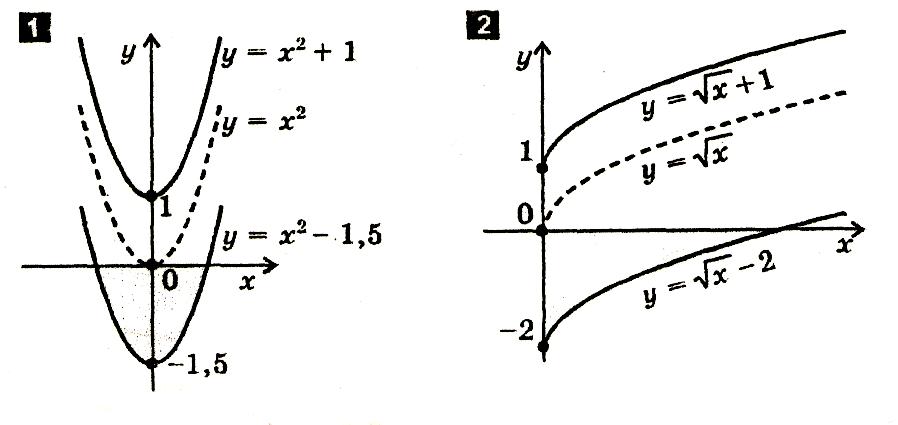
2. Паралельне перенесення вздовж осі х f(x)→f(x- а)

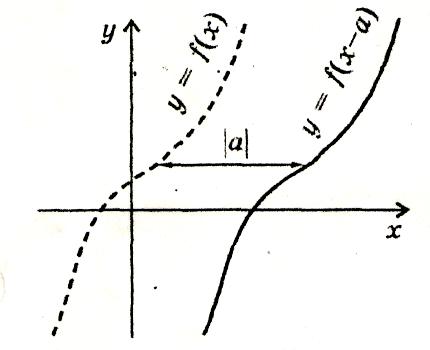
Графік функції у = f(х - а) дістається паралельним пере­несенням графіка функції у = f(x) вздовж осі х на |а| одиниць: праворуч, якщо а > 0, і лі­воруч, якщо а < 0.

3. Стиск і розтяг вздовж осі у f(x)→kf(x), де k › 0

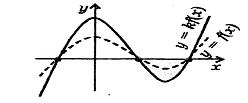
k › 1

Графік функції у =kf(х) дістається розтягом графіка функції у =f(х) вздовж осі у в k разів.

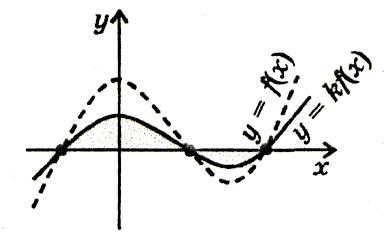
0 ‹ k ‹ 1

Графік функції у = kf(х) дістається стиском графіка функції у = f(х) вздовж осі у в 1/k разів.

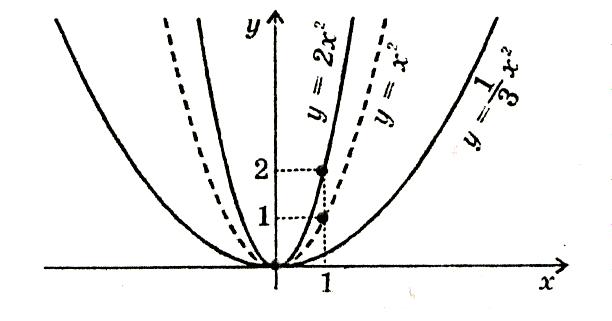
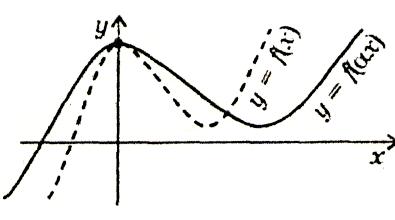
4. Стиск і розтяг вздовж осі х f(x)→f(ax), де а › 0

а › 1

Графік функції у =f(ах) дістається стиском графіка функції у =f(х) вздовж осі х в а разів.

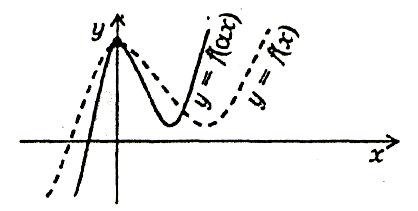
0 ‹ a ‹ 1

Графік функції y=f(ax)дістається розтягом графіка функції y=f(x) вздовж осі х в 1/а разів.

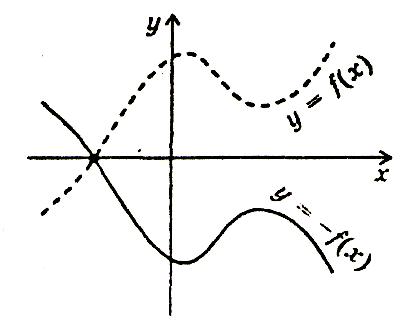
4. Перетворення симетрії відносно осі х f(x)= - f(x)

Графік функції у =-f(х) дістається перетворенням си­метрії графіка функції у =f(х) відносно осі х.

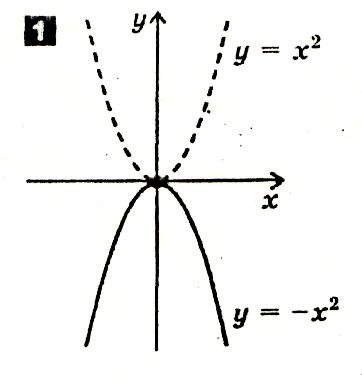
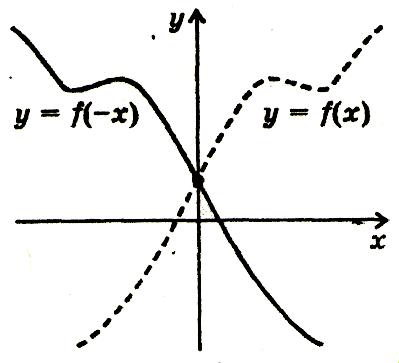
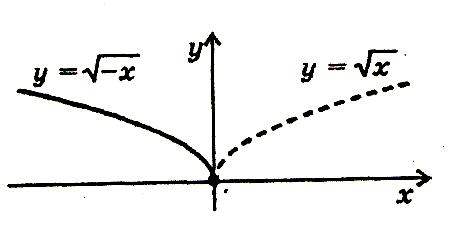
4. Перетворення симетрії відносно осі у f(x)=f(-x)

Графік функції у = f(-x) дістається перетворенням си­метрії графіка функції у = f(х) відносно осі у.

7. Побудова графіка функції у= │f(x)│

Частини графіка функції у = f(х), які лежать вище осі х і на осі х, залишаються без зміни, а частини, які лежать нижче осі х —симетрично відбиваються відносно цієї осі (вгору).

Побудова графіка функції у=f(│x│)

Частина графіка функції у = f(х), що лежить ліворуч осі у, вилучається, а частина, що лежить праворуч від осі у— залишається без зміни і, крім того, симетрично відбивається відносно осі у (ліворуч). Точка графіка, яка лежить на осі у, залишається незмінною.