Лабораторная работа №1 Вычисление погрешностей величин и результатов арифметических действий

Задание 1:

1. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры:

а) в узком смысле;

б) в широком смысле.

а) 0,374 : б) 4,348

2. Определить, какое приближенное равенство более точно.

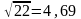
3. Округлить сомнительные цифры числа, оставив верные знаки:

а) в узком смысле;

б) в широком смысле.

a) 2,4543 : =0,0032 б) 24,5643 : =0,1 %

Задание 2:

Вычислите с помощью МК значение величины Z при заданных значениях параметров a,b, и с, используя «ручные» расчетные таблицы для пошаговой регистрации результатов вычислений, тремя способами:

а) по правилам подсчета цифр;

б) с систематическим учетом границ абсолютных погрешностей;

в) по способу границ

Сравните полученные результаты между собой, прокомментируйте различие методов вычислений:

0,0976

2,371

1,15874

Ход работы

Задание 1:

1.

1. 0,374 – в узком смысле x=0,374 х=0,0005 х=0,0013368 х=0,13%

2. 4,348-в широком смысле

x=4,348

∆x=0,001

х=0,0002299

х=0,023%

2.

1. √44=6,63

x₁=6,63324958

∆ x₁=|6,63324958-6,63|= 0,00324958

δx₁=0,0033/6,63=0,00049774=0,050%

2. √22=4,69

x₁=4,6904157

∆ x₁=|4,6904157-4,69|=0,0004157

δx₂=0,00042/4,69=0,0000895=0,0090%

0,0497% < 0,0895%

х₁ < х₂ => равенство √44=6,63 более точное.

Вывод: так как относительная погрешность приближения √22=4,69 больше, то равенство √44=6,63 является более точным.

3.

1. 22,553 – в узком смысле

x=22,553

∆=0,016

3: 0,0005<0,016 неверная

5: 0,005<0,016 неверная

5: 0,05>0,016 верная

x₁=22,5

х₁=|22,552-22,5|+0,016=0,068

5: 0,05<0,068 неверная

2: 0,05<0,068 верная

x₂=22

Δ x₂=|22,5-22|+0,068=0,568

2: 0,5<0,568 неверная

2: 5> 0,0568 верная

х₃=2*10

Δ x₃=|2*10-22|+0,568=2,568

2: 5>2,568 верная

22,553≈2*10

2. 24,5643 - В широком смысле

x=24,5643

х=0,1%

х=х|х|

х=0,0005*24,5643=0,01228

3: 0,0001<0,01228 неверная

4: 0,001<0,01228 неверная

6: 0,01>0,01228 верная

х₁=24,56

х₁=|24,5643 -24,56|+0,01228=0,01658

6: 0,01<0,01658 неверная

5: 0,1>0,01658 верная

x₂=24,5

х₁=|24,56-24,5|+0,01658=0,07658

5: 0,1>0,07658 верная

24,5643≈24,5

Z=

a=0,0976

b=2,371

c=1,15874

Задание 2:

а) по правилам подсчета цифр

Выражение	Значение	Комментарии
aс	0,0976*1,15874=0,113093
ac+b	0,113093+2,371=2,4841	При сложении приближенных чисел в результате верными следует считать те цифры, десятичным разрядам которых соответствуют верные цифры во всех слагаемых
b-c	2,371-1,15874=1,21226	При читании приближенных чисел в результате верными следует считать те цифры, десятичным разрядам которых соответствуют верные цифры во всех слагаемых
√b-c	√1,21226=1,1010	При извлечении квадратного корня в результате следует считать верными столько значащих цифр, сколько имелось верных значащих цифр в исходном числе
	2,4841/1,1010=2,2562	При делении приближенных чисел в результате верными следует считать столько значащих цифр, сколько имеет их приближенное данное с наименьшим количеством значащих цифр

Z=2,256

b) с систематическим учетом границ абсолютных погрешностей

a = 0,0976; a=0,0001

b = 2,371; b=0,001

c = 1,15874; с=0,00001

a	b	c	ac	ac+b	b-c	√b-c
0,0976	2,371	1,15874	0,113093	2,4841	1,21226	1,1010	2,2562
Δa	Δb	Δc	Δac	Δac+b	Δb-c	Δ√b-c	Δ
0,0001	0,001	0,00001	0,00011	0,00111	0,00101	0,00032	0,001649

с) по способу границ

0,00975<a<0,0977

2,370<b<2,372

1,15873<c<1,15875

НГ ВГ

ac=0,00975*1,15873=0,0113 ac=0,0977*1,15875=0,1132

ac+b=0,0113+2,370=2,3813 ac+b=0,1132+2,372=2,4852

b-c=2,370-1,15873=1,21127 b-c=2,372-1,15875=1,21325

√b-c=√1,21127=1,1006 √b-c=√1,21325=1,1015

=2,3813/1,1006=2,1636 =2,4852/1,1015=2,2562

2,1636< <2,2562

	a	b	c	ac	ac+b	b-c	√b-c
НГ	0,00975	2,370	1,15873	0,0113	2,3813	1,21127	1,1006	2,1636
ВГ	0,0977	2,372	1,15875	0,1132	2,4852	1,21325	1,1015	2,2562