7. Модели представления знаний. Извлечение и приобретение знаний.

Данные - это отдельные факты, характеризующие объекты, процессы и явления ПО, а также их свойства.

• D1 – данные как результат измерений и наблюдений.

• D2 – данные на бумажных носителях информации.

• D3 – модели и структуры данных.

• D4 – данные на языке описания данных.

• D5 – данные в компьютере

Знания – результат мыслительной деятельности человека, закономерности ПО (принципы, связи, законы), полученные в результате практической деятельности и профессионального опыта, позволяющие специалистам ставить и решать задачи в этой области.

• Z1 – знания в памяти человека как результат мышления.

• Z2 – бумажные носители знаний.

• Z3 – поле знаний – условное описание основных объектов ПО, их атрибутов и закономерностей,

• которые их связывают.

• Z4 – знания на языках представления знаний.

• Z5 – знания в компьютере.

Процедурные знания – это знания в алгоритмах, они управляют данными. Декларативные знания - представлены в структурах данных (таблицы, списки, предложения, записанные на языках представления знаний). Для хранения знаний используются базы знаний (БЗ).

Модели

1. Продукционная модель – модель правил «если-то».

2. Семантическая сеть – это ориентированный граф, вершины которого - это понятия, а дуги – отношения между ними.

3 типа отношений: класс – элемент класса, свойство – значение, пример элемента класса.

Классификация семантических сетей: а) по количеству типов отношений: однородная, неоднородная. б) по типам отношений: бинарные, n-арные.

3. Сеть фреймов – семантическая сеть, в которой объекты структурированы. Характеристики фреймов называются слотами. Самый главный слот – АКО.

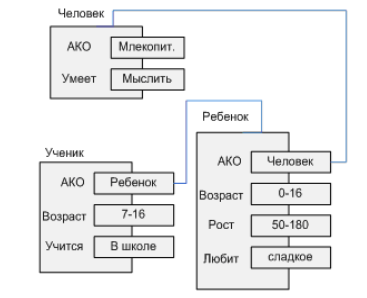
4. Формальные логические модели. ППП - предикат первого порядка. A,B,C -> Q,P

Извлечение и приобретение знаний

Извлечение знаний – выделение фрагментов модели предметной области (знаний) из потока информации, полученного из источника знаний. Приобретение знаний включает в себя две фазы: извлечение знаний из источника; наполнение БЗ.

8. Логико-лингвистические модели принятия решений при нечеткой исходной информации.

Нечеткое множество

Пусть Х – произвольное непустое множество ( X={x} ). Тогда нечетким подмножеством над

множеством Х называется множество пар для каждого х, где :X →[0,1] и называется функцией принадлежности нечеткого множества А, а Х называется базовым множеством ={<

Нечеткая переменная

Нечеткой переменной называется тройка <a,X, > где α – наименовании нечеткой переменной, Х –область определения нечеткой переменной, - множество, которые определяют смысл этой переменной ={<

Лингвистическая переменная

Под лингвистической переменной L будем понимать L=<β,T,X,G,M>, где β-наименование лингвистической переменной, T-базовое(исходное) множество её значений(терм множества), представляющее собой наименование нечетких переменных, областью определения каждой из которых является множество X; G-синтаксическая процедура(грамматика), которая позволяет оперировать элементами исходного терм-множества для того, чтобы генерировать новые осмысленные термы; M- лингвистическая процедура, позволяющая превратить каждое новое значение, сгенерированное грамматикой в нечеткую переменную, т.е. придать ей смысл.

Логико-лингвистические модели

Логико-лингвистические методы описания систем основаны на том, что поведение исследуемой системы описывается в естественном (или близком к естественному) языке в терминах лингвистических переменных. Входные и выходные параметры системы рассматриваются как лингвистические переменные, а качественное описание процесса задается совокупностью высказываний следующего вида:

: если < > и/или < > > и/или … и/или < > >, то < > > и/или … и/или < > ,

: если < > и/или < > > и/или … и/или < > >, то < > > и/или … и/или < > ,

: если < > и/или < > > и/или … и/или < > >, то < > > и/или … и/или < > .

где < >, i=1,2,..,k j=1,2,…,m- составные нечеткие высказывания первого и второго типов, определенные на значениях входных лингвистических переменных, a < > i = 1,2,..,k j=1,2,…,n –нечёткие высказывания первого и второго типов, определенные на значениях выходных лингвистических переменных. Эта совокупность правил носит название нечеткой базы знаний.

Композиционная модель вывода

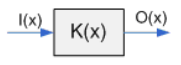
I(x) -лингв. перем. входные

O(x) - лингв. перем. выходные

K(x) – коэффициент передачи – некоторая сетка

9. Методы поиска решений на И/ИЛИ-графах. Априорные знания и эвристические функции.

Представление задач в пространстве состояний предполагает задание ряда описаний: состояний, множества операторов и их воздействий на переходы между состояниями, целевых состояний. Пространство состояний можно представить как граф, вершины которого помечены состояниями, а дуги - операторами. Таким образом, проблема поиска решения задачи при планировании по состояниям представляется как проблема поиска на графе пути из А в В. Рассмотрим задачу построения слова из некоторого множества букв. Обладая набором операций установки букв, можно сформировать пространство состояний. Предположим, что множество доступных букв включает Т, С и А. На каждом уровне графа мы будем добавлять по одной определенной букве. Каждая ветвь, исходящая из узла, соответствует установке буквы в определенную позицию в последовательности, а эта последовательность должна образовать осмысленное слово.

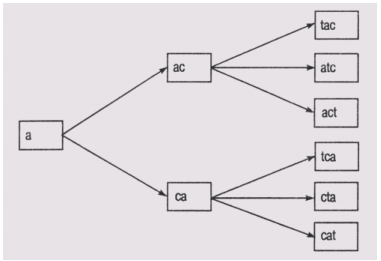Дерево пространства состояний

Различаются слепые и направленные методы поиска пути. Слепой метод имеет два вида: поиск в глубину, поиск в ширину. В алгоритме поиска в ширину просматриваются последовательно состояния, представленные узлами одного и того же уровня на графе, а в алгоритме поиска в глубину просматриваются состояния на одном пути, а затем происходит возврат назад на один уровень и формируется следующий путь.

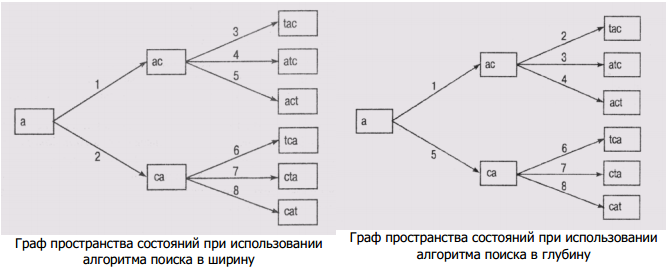
На обоих рисунках числа на дугах графа указывают номер шага, на котором формируется тот узел(состояние), для которого эта дуга является входящей. Оба алгоритма завершат работу (найдут конечное состояние) после формирования узла "act", а не "cat". Но алгоритму поиска в ширину придется для этого сформировать и проанализировать пять состояний, а алгоритму поиска в глубину — четыре.

Алгоритм поиска в ширину отыскивает решение, путь к которому на графе — кратчайший, если таковое существует. Алгоритм поиска в глубину может быстрее найти решение. Но этот алгоритм может никогда не закончиться, если пространство состояний бесконечно.

Поскольку слепой поиск возможен только в небольшом пространстве вариантов, необходим способ направленного поиска. Если такой способ использует при поиске пути на графе в пространстве состояний некоторых знаний, специфических для конкретной предметной области, его принято называть эвристическим поиском.

Простая форма эвристического поиска — это восхождение на гору. В процессе поиска в программе использует некоторая оценочная функция, с помощью которой можно грубо оценить, насколько "хорошим" (или "плохим") является текущее состояние. Затем можно применить ту же функцию для выбора очередного шага, переводящего систему в следующее состояние.

Лучшими свойствами обладает другая форма эвристического поиска, которая получила наименование сначала наилучший. Так же, как и в варианте восхождения на гору, в нашем распоряжении имеется оценочная функция, с помощью которой можно сравнивать состояния в пространстве состояний. Основное же отличие нового метода от ранее рассмотренного состоит в том, что сравниваются не только те состояния, в которые возможен переход из текущего, но и все, до которых "можно достать".

Такой алгоритм, естественно, требует значительно больших вычислительных ресурсов, но идея состоит в том, чтобы принимать во внимание не только ближайшие состояния, а оценить как можно больший участок пространства состояний и быть готовым, в случае необходимости, вернуться туда, где мы уже были, и пойти другим путем, если ближайшие претенденты не сулят существенного прогресса в достижении цели.

Программирование на языке высокого уровня (Неудачин И.Г.)