3 Регрессия главных компонент

Для построения модели с помощью регрессии главных компонент необходимо вычислить главные компоненты ковариационной матрицы независимых переменных. Результаты вычисления представлены в таблице 7. В последней строке таблицы указана дисперсия соответствующая главным факторам.

Таблица 7 – Весовые коэффициенты главных компонент (собственные состояния)

Исходные факторы		Главные компоненты
		1	2	3	4	5	6	7
GR	x1	0,8648	0,3235	-0,2502	0,2892	-0,0317	0,0143	0,0003
OR	x2	-0,2462	0,9318	0,1975	-0,1462	-0,1036	-0,0057	-0,0007
RVN	x3	0,0661	0,0753	0,0309	-0,1747	0,8218	0,2117	-0,4881
TS	x4	0,4308	-0,1322	0,6117	-0,6252	-0,1606	-0,0779	-0,0075
CC	x5	0,0199	0,0138	0,1502	-0,4252	0,4518	-0,3333	0,5006
SB	x6	0,0237	0,0006	0,0469	-0,0642	0,06769	0,852	0,5125
Дисперсия гл.комп.	ГК	646,823	73,441	15,295	8,229	1,081	0,038	0,001

На рис. 6 представлено графическое отображение главных компонент независимых переменных.

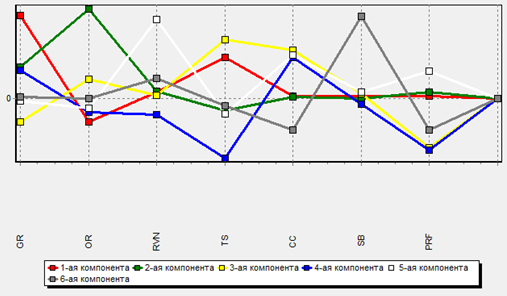
Рисунок 6 – Главные компоненты

Модель, поостренная с помощью регрессии главных компонент, имеет вид:

где 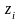— главные компоненты. Главные компоненты представляют комбинацию исходных факторов.

И т.д. для каждого их компонент.

Отличие главных компонент от исходных факторов заключается в том, что главные компоненты являются статистически независимыми, т.е. корреляция между ними равна нулю.

Таблица 8 — Характеристики регрессионной 6-ти факторной модели

(главные факторы)

Главные факторы	Коэффициенты регрессии	Коэффициент значимости
	1,266734	195,826
1-ый фактор	0,022449	93,957
2-ой фактор	0,060451	120,944
3-ий фактор	-0,519377	-368,932
4-ый фактор	-0,537111	-290,869
5-ый фактор	0,274296	49,818
6-ой фактор	-0,373030	7,824

Как видно из таблицы 8 анализ значимости коэффициентов регрессионной модели показывает, что все коэффициенты модели являются существенно значимыми. Отбросим 6-й главный фактор, так как он является статистически наименее значимым. Поэтому с целью улучшения качества модели построим модель на первых пяти главных факторах. В табл. 9 представлены коэффициенты 5-и факторной регрессионной модели.

Таблица 8 — Характеристики регрессионной 5-ти факторной модели

(главные факторы)

Главные факторы	Коэффициенты регрессии	Коэффициент значимости
	1,272389	103,358
1-ый фактор	0,022652	46,797
2-ой фактор	0,030765	42,301
3-ий фактор	-0,517944	-164,541
4-ый фактор	0,537324	-125,206
5-ый фактор	0,280061	23,658

Как видно из таблицы все коэффициенты модели являются существенно значимыми. Отбросим 5-ый главный фактор, так как он является статистически наименее значимым. Поэтому с целью улучшения качества модели построим модель на первых четырех главных факторах. В табл. 9 представлены коэффициенты 4-х факторной регрессионной модели.

Таблица 8 — Характеристики регрессионной 4-х факторной модели

(главные факторы)

Главные факторы	Коэффициенты регрессии	Коэффициент значимости
	1,224062	22,500
1-ый фактор	0,020964	10,015
2-ой фактор	0,057374	9,871
3-ий фактор	0,544393	-37,160
4-ый фактор	-0,556551	-25,150

Как видно из таблицы все коэффициенты модели являются существенно значимыми. Прежде чем отбросить следующий наименее значимый коэффициент, обратимся к анализу полученных ошибок при построении разнофакторных моделей, оценив целесообразность сокращения количества главных факторов при моделировании.

В таблице 9 представлены значения ошибок для моделей, с различным числом факторов.

Таблица 9— Ошибки прогнозирования моделей

Число главных факторов	MAD	MSE	SSE	MAPE%	MPE %	MSEN %
6	0,030	0,001	0,087	-0,012	0,045	0,813
5	0,095	0,011	0,281	-0,720	0,897	2,618
4	0,333	0,2690	1,372	-5,689	-2,810	12,764

Анализируя таблицу 12, можно заметить, что модель 6-ти факторная модель имеет наиболее низкие ошибки прогнозирования, и при сокращении количества факторов точность модели теряется.

Отметим, что данная модель полностью совпадает с классической 6-и факторной регрессионной моделью.

Таким образом, построена регрессионная модель прогнозирования прибыли гостиницы «Планета». В ходе работы было выявлено, что 6-и факторная модель имеет более высокие коэффициенты значимости и наименьшие ошибки прогнозирования.

На рисунке 7 — изменение прибыли для 6-и факторной модели (сплошная линия) и фактические значения (пунктирная линия) практически совпадают.

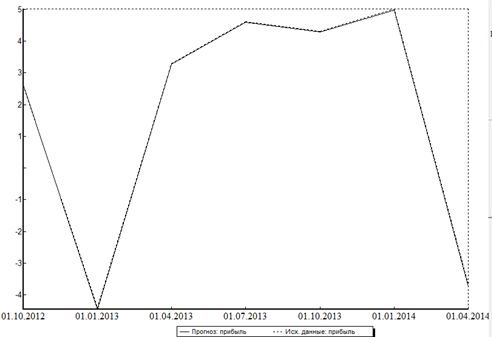
Рисунок 7 — Изменение прибыли на тестовой выборке

(6-и факторная модель)

ЗАКЛЮЧЕНИЕ

В ходе работы была построена модель зависимости прибыли гостиницы «Планета». Анализ прибыли предприятия с помощью полученной модели показывает о зависимости прибыли в большей степени от выручки, затрат на строительсво и ремонт, а также от количества сотрудников предприятия. Однако, это не означает, что изменение лишь этих факторов формирует динамику изменения прибыли – при построении наиболее точной модели необходимо учитывать все экономические показатели.

В ходе работы были построены модели, с различными наборами факторов. При этом исследование исходных и главных факторов дают одинаковые результаты: наиболее лучшими параметрами обладает 6-ти факторная модель, которая имеет наиболее низкие значения ошибок.