2.4 Качество классической регрессионной модели

Для доверительного интервала 99% (уровень значимости 1%) и числе степеней свободы (число наблюдений) 30 табличное значение коэффициента Стьюдента равно 2,75, для 95% доверительного интервала (5% уровень значимости) коэффициент Стьюдента равен 2,042. Поэтому все коэффициенты больше 2,75 являются статистически значимыми, а те которые лежат ниже 2,75 — статистически не значимы.

Как видно из таблицы коэффициенты 1-объем номерного фонда, 2-загрузка гостиницы и 4-количество сотрудников являются статистически незначимыми. Статистически значимыми являются выручка, затраты на строительство и ремонт, а также фонд оплаты труда.

2.5 Точность классической регрессионной модели

Построенная модель проверяется на диапазоне, который не использовался при построении регрессионной модели, т.е. на основе последних 6 наблюдений. Прогнозные значения сравниваются с исходными данными. В результате вычислены шесть видов ошибок:

• Среднее абсолютное отклонение (Mean Absolute Derivation, MAD) – измеряет точность пргоноза. Усредняя величины его ошибок,

• Среднеквадратическая ошибка (Mean Squared Error, MSE) – подчеркивает большие ошибки прогноза,

• Средняя стандартная ошибка (SSE),

• Средняя абсолютная ошибка в процентах (Mean Absolute Percentage Error, МАРЕ) – показывает, насколько велики ошибки прогноза в сравнении с действительными значениями ряда,

• Средняя процентная ошибка (Mean Percentage Error, MPE) – показывает, является ли метод прогнозирования смещенным (в нашем случае прогноз немного последовательно недооценивающий, практически не смещен),

• Стандартная ошибка оценки (Mean Standart Error MSEN) – показывает стандартное отклонение для значений остатков.

Ошибки, полученные на тестовой выборке, представлены в таблице 4. На рисунке 3 показаны изменения прибыли на тестовой выборке (пунктирная линия) и изменения прибыли, вычисленные с помощью 6-ти факторной модели. Стоит отметить, что величины ошибок очень малы.

Таблица 4 — Ошибки прогнозирования модели

Число исходных факторов	MAD	MSE	SSE	MAPE%	MPE %	MSEN %
6	0,030	0,001	0,087	-0,012	0,045	0,813

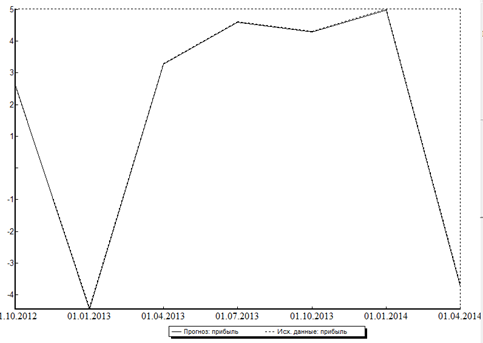
Рисунок 4 — Изменение прибыли на тестовой выборке (6-ти факторная модель)

2.6 Изменение качества классической регрессионной модели

Анализ значимости коэффициентов регрессионной модели показывает, что объем номерного фонда, загрузка гостиницы и количество сотрудников являются статистически незначимым (при уровне значимости 1%). Статистически значимыми являются выручка, затраты на строительство и ремонт, а также фонд оплаты труда. С целью улучшения модели исключим данные незначимых параметров. В результате получаем 3-х факторную регрессионную модель с коэффициентом детерминации 2,75. В таблице 5 представлены значения 3-х факторной модели. Как видно из таблицы все коэффициенты являются статистически значимыми.

Таблица 5 — Характеристики регрессионной 3-х факторной модели

Исходные факторы	Коэффициенты регрессии	Коэффициент значимости
	1,154637	4,534
RVN	-1,488766	-3,253
CC	1,958704	3,697
SB	-5,805153	-4,057

Анализ значимости коэффициентов регрессионной модели показывает, что коэффициенты для всех независимых факторов являются статистически значимым. Поэтому улучшение модели не проводится.

В таблице 6 представлены значения ошибок для 6-ти факторной и 3-х факторной моделей, а на рисунке 4 — изменение прибыли для 6-ти факторной модели (сплошная линия) и фактические значения (пунктирная линия).

Таблица 6 — Ошибки прогнозирования моделей

Число исходных факторов	MAD	MSE	SSE	MAPE%	MPE %	MSEN %
6	0,030	0,001	0,087	-0,012	0,045	0,813
3	4,110	22,242	12,478	80,166	80,166	166,056

В таблице 6 представлены ошибки прогнозирования, полученные на тестовой выборке, для 6-ти и 3-х факторной модели. Как видно из таблицы, ошибки прогнозирования 6-ти факторной модели ниже, и это означает, что качество модели выше, и улучшать ее не следовало.

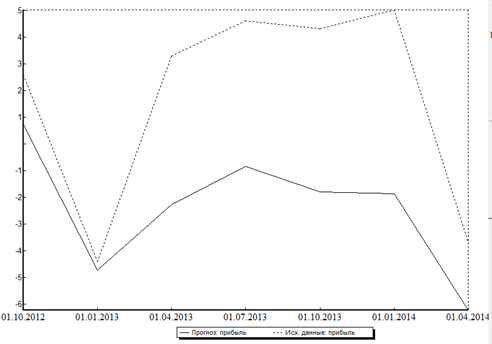
Рисунок 5 – Изменение прибыли на тестовой выборке (3-х факторная модель)