3. Анализ собственных состояний

Итак, нами выделено семь независимых состояний, в рамках которых исходные факторы могут изменяться только определенным образом. Исходя из выбранного ограничения «увеличение загрузки гостиницы должно способствовать увеличению выручки», модель будет описываться 1, 3, 4, 5 6-ой главными компонентами.

Таким образом, анализ выделенных независимых составляющих позволяет сделать вывод, что увеличение загрузки гостиницы приводит к росту выручки только в рамках 1, 3, 4, 5 6-ой главных компонент, т.е. именно эти состояния удовлетворяет требованию эталонной модели. В рамках этой модели показатели выручки будем вычисляться через главные компоненты по формуле

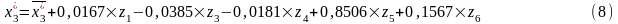Где 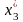– среднее значение прибыли, z₁, z₃, z₄, z₅, z₆, — главные компоненты.

1.4 Анализ зависимости выручки предприятия от загрузки

На рисунках 1 и 2 показано сравнение зависимости выручки предприятия от загрузки, полученное в рамках эталонной модели предприятия (пунктирная линия) и фактических значений (сплошная линия).

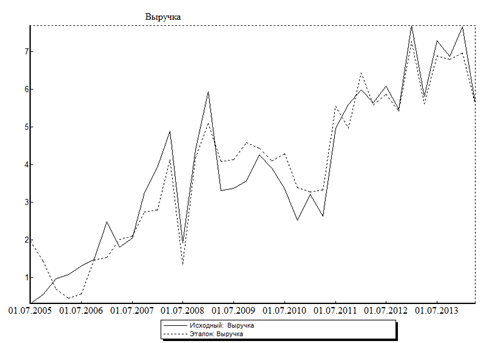
Рисунок 1 — Изменение выручки: прогнозируемые и фактические значения

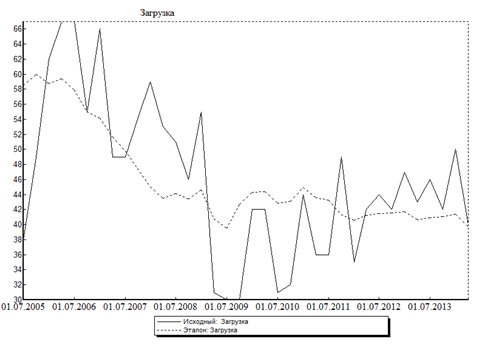
Рисунок 2 — Изменение загрузки: прогнозируемые и фактические значения

2 Прогнозирование прибыли гостиницы «планета»

Стандартным инструментом прогнозирования является регрессионный анализ. Поведение зависимой переменной объясняется с помощью комбинации переменных. В этом случае используется множественная регрессия. Если независимые переменные являются высоко коррелированными, то регрессионные модели трудно интерпретировать. Кроме того, высоко коррелированные переменные не обладают независимым поведением, что приводит к проблеме мультиколлинеарности в регрессионном анализе. В качестве показателей, описывающих экономическое состояние гостиницы «Планета»» выбраны объем номерного фонда, загрузка гостиницы, выручка, количество сотрудников, затраты на строительство и ремонт, фонд оплаты труда.

2.1 Классическая регрессионная модель

Строится классическая регрессионная модель, которая описывается выражением (10)

где Х₇ — прибыль предприятия, x₁ – объем номерного фонда, х₂ – загрузка гостиницы, х₃ – выручка, х₄ – количество сотрудников, х₅ – затраты на строительство и ремонт, х₆ – фонд оплаты труда.

2.2 Исходные данные

Диапазон наблюдений 36 точек, с 1 июля 2005 года до 1 апреля 2014 года с шагом в один квартал. На рисунке 3 изображена динамика изменения прибыли за весь период существования предприятия.

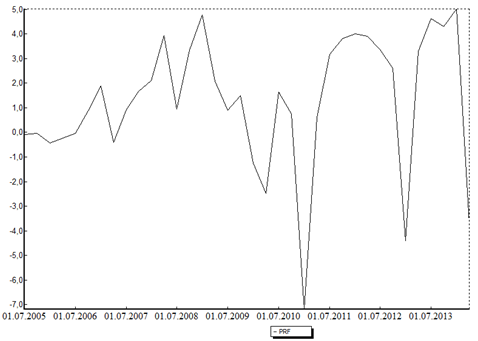
Рисунок 3 — Изменение прибыли предприятия

2.3 Построение классической регрессионной модели

Коэффициенты классической регрессионной модели показаны в таблице 3. Первая строка таблицы содержит значение для коэффициента . В этой же таблице показаны коэффициенты значимости.

Таблица 3 — Линейная регрессионная 6-ти факторная модель

Исходные факторы	Коэффициенты регрессии	Коэффициент значимости
	-0.089285	-13.803
GR	-0.000363	-0.596
OR	0.000631	1.025
RVN	0.230308	17.009
TS	0.004736	1.405
CC	-0.239955	-16.471
SB	-0.288688	-7.050