Введение

Для осуществления транспортных работ необходимо знать кратчайшие расстояния между автотранспортным предприятием (АТП), пунктами отправления и пунктами получения грузов, объем перевозимого груза, грузооборот, грузопоток и их неравномерность. Эти данные является основанием для выбора подвижного состава, определения расхода топлива и смазочных материалов, заработной платы водителей, заключения договора с клиентом на перевозку и определения размера оплаты за выполненный объем транспортных работ.

Дано: перевести из с. Коченево(11) Новосибирской области во все другие райцентры области запчасти в количестве 100 тонн за 10 дней.

1. Построение схемы транспортной сети.

Перед началом моделирования транспортной сети провожу анализ карты НСО.

На карте нахожу места (точки) размещения АТП, отправителей и получателей грузов. Все эти точки нумерую. В нашем задании мы нумеруем пункты, так же как они пронумерованы на карте Новосибирской области.

На чистый лист бумаги наношу координатную сетку как на карте НСО, в масштабе с карты переносят точки размещения АТП, отправителей, получателей. Эти точки являются вершинами будущего графа. Каждой вершине графа присваивается цифра райцентра АТП, отправителя или получателя груза, нанесенная на карте.

Затем вершины связываю звеньями сети и дугами в зависимости от организации движения в области. При этом учитывают дороги, улицы и проезды, имеющие усовершенствованные покрытия. Если вершины связаны несколькими параллельными проездами, то на модели транспортной сети их заменяют одним звеном.

После анализа выбираю кратчайшие маршруты движения по улицам города (дорогам области) между каждыми двумя вершинами. Расстояние на карте между точками измеряют специальным прибором — курвиметром. Фактическое расстояние между точками находят путем умножения показания курвиметра на масштаб карты. Найденное кратчайшее расстояние между двумя вершинами графа записывают на звене (дуге), соединяющем эти вершины. Таким образом, получают схему транспортной сети. Схема транспортной сети НСО представлена на чертеже ОАПиБД.00.10.01.

2. Определения кратчайших расстояний между вершинами схемы транспортной сети.

При определении кратчайших расстояний от заданной вершины (вершина № 11) до всех других все множество вершин сети разбивают на три группы:

- в группу 1 входят вершины, до которых кратчайшие расстояния уже найдены;

- в группу 2 входят вершины, смежные (связанные с другой) с вершинами первой группы;

- в группу З входят все остальные вершины.

Нахождение кратчайших расстояний от одной (вершины11) до всех остальных вершин для сети состоит из нескольких этапов. АТП размещена в вершине 11.

Этап О. Перед первым этапом в 1-ю группу вершин входит только начальная вершина 14, где находится АТП. Кратчайшёе расстояние от АТП до нее равно 0 км. Остальные вершины входят в группу 3, так как расстояния до них не определены и равны большому числу, которое обозначают буквой М (таблица 1).

№ вершины	11	4	12	10	13	14	23	24	9	30	5	3	22	29	25	17	21	28	8	20	16	7	2	19	27	15	1	6	18	26
Расстояние км	0	М	М	М	М	М	М	М	М	0	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М
№ предш. вершины	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

В последней строке таблицы 1 фиксируем номера вершин, предшествующих

данным в кратчайшем расстоянии до них. У вершины 11 нет предшествующих вершин, поскольку она является начальной. У остальных вершин предшествующие вершины пока не определены. В результате все элементы последующей строки равны О.

Этап 1. На рисунке 1 находим вершины, смежные с вершиной 11. К ним относятся вершины 4,12,10 которые из группы З переношу группу 2. Расстояние до них определяют по формуле, км

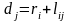(1)

где d_j - расстояние от начальной вершины до j-той вершины;

r_i — кратчайшее расстояние от начальной вершины до i-той

l_ij — длина ребра, связывающего i-ю вершину с j-той.

Подставляя данные в формулу 1, получают:

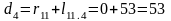
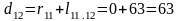
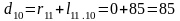
Полученные расстояния записывают в таблицу 2.

Таблица 2 – Анализ транспортной сети 1 этапа

№ вершины	11	4	12	10	13	14	23	24	9	30	5	3	22	29	25	17	21	28	8	20	16	7	2	19	27	15	1	6	18	26
Расстояние км	0	53	63	85	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М
№ предш. вершины	0	11	11	11	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

В последней строке таблицы 2 для вершин 4,12,10 в качестве предшествующей запишем вершину 11. Среди расстояний до вершин группы 2 выбираю минимальное. В таблице 2 им является расстояние до вершины 4. Кратчайшее расстояние до нее r₄ =53 км.

Этап 2. Ищем вершины, смежные с вершиной 4. Это вершина 12.

Вершину 11 не рассматривают, так как она входит в 1-ю группу. Для остальных

вершин вычисляют расстояние по формуле (1):

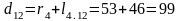
Вершина 12 уже находятся в группе 2. Вновь вычисленное для нее расстояние больше, чем было в таблице 2. Поэтому оставляют его прежним.

Таблица 3 – Анализ транспортной сети 2 этапа

№ вершины	11	4	12	10	13	14	23	24	9	30	5	3	22	29	25	17	21	28	8	20	16	7	2	19	27	15	1	6	18	26
Расстояние км	0	53	63	85	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М	М
№ предш. вершины	0	11	11	11	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

По таблице 3 ищем минимальное расстояние до вершин, входящих в группу 2. Им оказывается расстояние до вершины 12. Вершина 12 переводится в группу 1. Кратчайшее расстояние до нее r₁₂ =63 км смежной с ней является вершина 13,14,23,24. Далее расчеты ведутся аналогично и будут представлены в виде формул и таблиц.