48. Инерциальные и неинерциальные системы отсчета

Инерциальная система отсчета — система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно или покоятся. Эквивалентной является следующая формулировка, удобная для использования в теоретической механике: «Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным». Законы Ньютона, а также все остальные аксиомы динамики в классической механике формулируются по отношению к инерциальным системам отсчёта.

Неинерциальная система отсчета — система отсчёта, в которой не выполняется первый закон Ньютона — «закон инерции», говорящий о том, что каждое тело, в отсутствие действующих на него сил, движется по прямой и с постоянной скоростью. Всякая система отсчета, движущаяся с ускорением или поворачивающаяся относительно инерциальной, является неинерциальной. Второй закон Ньютона также не выполняется в неинерциальных системах отсчёта. Для того, чтобы уравнение движения материальной точки в неинерциальной системе отсчёта по форме совпадало с уравнением второго закона Ньютона, дополнительно к «обычным» силам, действующим в инерциальных системах, вводят силы инерции.

49. Элементарный импульс силы

Векторная мера действия силы, равная произведению силы на элементарный промежуток времени ее действия.

Импульс силы за столь малый промежуток времени, при котором изменением силы можно пренебречь.

50. Теорема о переносе вектора силы в произвольную точку пространства

НЕ  ИЗМЕНЯЯ  ДЕЙСТВИЯ  СИЛЫ  НА  ТВЕРДОЕ  ТЕЛО,  СИЛУ  МОЖНО  ПЕРЕНЕСТИ ПАРАЛЛЕЛЬНО  САМОЙ  СЕБЕ  В  ЛЮБУЮ  ТОЧКУ  ТЕЛА - ЦЕНТР  ПРИВЕДЕНИЯ,  ПРИЛОЖИВ  ПРИ  ЭТОМ  К  ТЕЛУ  ПАРУ  СИЛ  С  МОМЕНТОМ,  РАВНЫМ  МОМЕНТУ  ПЕРЕНОСИМОЙ   СИЛЫ  ОТНОСИТЕЛЬНО  ЦЕНТРА ПРИВЕДЕНИЯ. 

51. Элементарная сила работы

Элементарной работой силы    называется скалярная величина:

,

где   - проекция силы    на касательную к траектории, направленную в сторону перемещения точки, а ds- бесконечно малое перемещение точки, направленное вдоль этой касательной.

Данное определение соответствует понятию о работе, как о ха­рактеристике того действия силы, которое приводит к изменению модуля скорости точки. В самом деле, если разложить силу   на составляющие   и  , то изменять модуль скорости точки будет только составляющая  , сообщающая точке касательное ускорение. Составляющая же   или изменяет направление вектора скорости v (сообщает точке нормальное ускорение), или, при несвободном дви­жение изменяет давление на связь. На модуль скорости составляю­щая   влиять не будет,  т.е., как говорят, сила   «не будет про­изводить работу».

Замечая, что  , получаем:

.                                            

Таким образом, элементарная работа силы равна проекции силы на направление перемещения точки, умноженной на элементар­ное перемещение ds или элементарная работа силы равна произведению модуля силы на элементарное перемещение ds и на косинус угла между направлением силы и направлением перемещения.

(51) Работа силы на конечных перемещениях

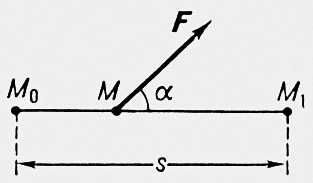
 Работа силы на конечном перемещении определяется как интегральная сумма элементарных работ и при перемещении M₀M₁выражается криволинейным интегралом: или