35. Равнодействующая система сил

1. Равнодействующая система сил

РАВНОДЕЙСТВУЮЩАЯ системы сил - сила, оказывающая на твердое тело такое же механическое действие, как и данная система приложенных к телу сил. В простейших случаях (напр., для сил, приложенных в одной точке или расположенных в одной плоскости) равнодействующую можно найти, последовательно применяя закон параллелограмма сил. Равнодействующую имеет не всякая система сил; напр., пара сил или две силы, не лежащие в одной плоскости, равнодействующей не имеют.

36.Пара сил

ПАРА СИЛ - две равные по величине и противоположные по направлению параллельные силы, приложенные к одному телу. Пара сил не имеет равнодействующей. Кратчайшее расстояние между линиями действия сил, образующих пару сил, называют плечом пары. Действие пары сил на тело характеризуется моментом пары сил - произведением одной из сил на плечо.

37. Аксиома параллелограмма в статике

  Не меняя cостояния тела, две силы, приложенные к одной его точке, можно заменить одной равнодействующей силой, приложенной в той же точке и равной их геометрической сумме

Другими словами, равнодействующую R можно построить как диагональ параллелограмма со сторонами, сов­падающими с F₁ и F₂. Модуль равнодействующей определится равенством R=(F₁²+F₂²+2F_lF₂cosa)^1/2, где а—угол между данными векторами F₁ и F₂. Аксиома применима к любым телам. 

38. Основной закон динамики точки

Основной закон динамики (второй закон Ньютона) материальной точки имеет вид F=,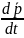 где – результирующая сила, действующая на материальную точку массы  m, = m – импульс материальной точки.

В случае m = const основной закон динамики принимает вид = m

37. Аксиома параллелограмма.

Не меняя cостояния тела, две силы, приложенные к одной его точке, можно за­менить одной равнодействующей силой, приложен­ной в той же точке и равной их геометрической сумме.

(Другими словами, равнодействующую R можно построить как диа­гональ параллелограмма со сторонами, сов­падающими с F₁ и F₂₎

38. Основной закон динамики.

39.

Условия равновесия сходящейся системы сил.

в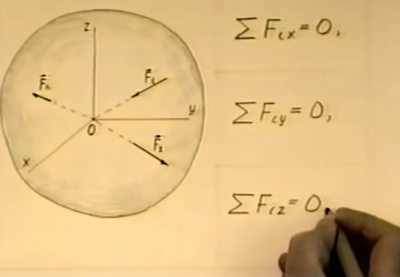 екторная форма:

Где R-равнодействующая сила

Fk – вектор k силы. K = 1;n

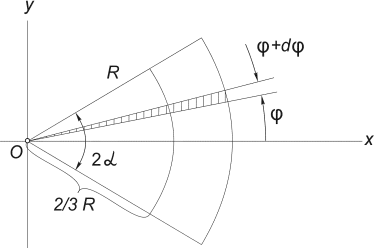
40.Центры тяжести. (x_c,y_c) – координаты центра тяжести.

• Круговой сектор

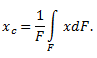смотри дальше!

y_c = 0 – очевидно.

Интеграл легче всего выразить, разбивая область интегрирования на элементарные секторы с углом dφ. Такой сектор можно заменить треугольником с основанием, равным Rdφ и высотой R. Площадь такого треугольника dF=(1/2)R²∙dφ, а его центр тяжести находится на расстоянии 2/3R от вершины, поэтому положим x = (2/3)R∙cosφ.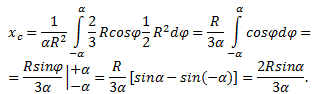 

• Треугольника

Центр тяжести треугольника лежит в точке пересечения его медиан, которая, как известно, отделяет от каждой медианы третью часть, считая от соответствующей стороны.

41. Закон сохранения количества движения (закон сохранения импульса).

Из теоремы об изменении количества движения системы можно получить следую­щие важные следствия:

1) Пусть сумма всех внешних сил, действующих на замкнутую систему, равна нулю:

Тогда из уравнения   следует, что Q= =const. Таким образом, если сумма всех внешних сил, действующих на замкнутую систему, равна нулю, то вектор количества движения (импульса) системы будет постоянен по модулю и направлению.

2) Пусть внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например Оx) равна нулю:

Тогда из уравнения   следует, что при этом Q_x=const. Таким образом, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения (импульса) системы на эту ось есть величина постоянная.

Эти результаты и выражают закон сохранения количества движения системы: при любом характере взаимодействия тел, образующих замкнутую систему, вектор полного импульса этой системы все время остается постоянным.