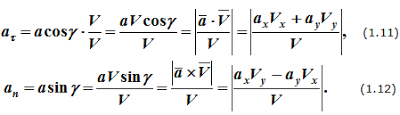23. Абсолютное ускорение точки

Движение, совершаемое точкой по отношению к неподвижной системе отсчета O₁x₁y₁z₁, называется абсолютным или сложным. Траектория  этого движения называется абсолютной траекто­рией, скорость - абсолютной скоростью (обозначается  ) и ускорение - абсолютным ускорением (обозначается  ). Равенство

представляет теорему сложения ускорений в случае, когда переносное движение является произвольным: абсолютное ускорение точки равно векторной сумме переносного, относительного и поворотного ускоре­ний. Эту теорему часто называют теоремой Кориолиса.

24. Найти производную по времени от V×ƭ¯ (тау) – единичный вектор касательной к траектории

Выражение для тангенциального ускорения можно найти, продифференцировав по времени вектор скорости, представленный в виде   через единичный вектор касательной  :

где первое слагаемое — тангенциальное ускорение, а второе — нормальное ускорение.

Здесь использовано обозначение   для единичного вектора нормали к траектории и   - для текущей длины траектории ( ); в последнем переходе также использовано очевидное

25 . Естественный способ задания движения точки (что включает в себя)

1.1.3 Естественный способ задания движения точки

Рисунок 1.4

На рисунке 1.4:

τ-орт касательной;

n-орт нормали;

b-орт бинормали;

     При естественном способе задания движения предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении.

     Единичные орты  τ, n ,b определяют направление соответствующих осей в каждой точке кривой.

Рисунок 1.5

     Чтобы задать закон движения точки естественным способом необходимо:

1) знать траекторию движения;

2) установить начало отсчета на этой кривой;

3) установить положительное направление движения;

4) дать закон движения точки по этой кривой, т.е. выразить расстояние от начала отсчета до положения точки на кривой в данный момент времени ∪OM=S(t) .

 Зная эти параметры можно найти все кинематические характеристики точки в любой момент времени (рисунок 1.5).

     

   Скорость точки определяется по формулам (1.9)

                                          V=τ⋅dS/dt,    V=dS/dt.   (1.9)

      Первая формула определяет величину и направление вектора скорости, вторая формула только величину.

     Ускорение определяется как производная от вектора скорости:

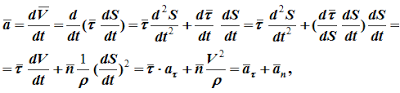
   т.е.  a=a_τ+a_n.    (1.10)

     В формуле (1.10)

     a_τ=τ⋅dV/dt=τ⋅d²S/dt², a_τ=dV/dt=τ⋅d²S/dt²- касательное ускорение; оно характеризует быстроту изменения величины скорости точки;

     a_n=n⋅V²/ρ, a_n=V²/ρ - нормальное ускорение точки; характеризует быстроту изменения направления вектора скорости;

    ρ - радиус кривизны траектории в данной точке (например, для окружности:ρ=R  , для прямой линии ρ=∞ ).

     Полное ускорение точки определяется следующим образом (рисунок 1.5):

     Выше отмечалось,  что всегда можно перейти от одного способа задания закона движения точки к другому. Поэтому, преобразовывая одни и те же формулы, можно получить другое их написание.

    Например,  

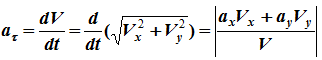
или   a_τ=acosγ (рисунок 1.5).       

    Далее