1. Скорость точки

Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки.

Скоростью точки в данный момент времени t называется векторная величина v¯, к которой стремится средняя скорость v¯ (cp) при стремлении промежутка времени ∆t к нулю:

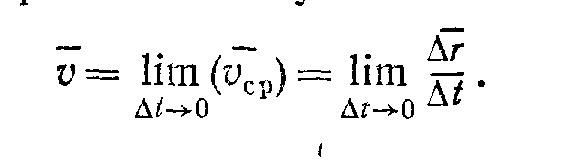
Предел отношения представляет собой первую производную от вектора r¯ по аргументу t и обозначается, как и производная скалярной функции, символом Окончательно получаем

2.Радиус-вектор точки.

Пусть точка М движется по отношению к некоторой системе отсчета Оxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор r¯, проведенный из начала координат О в точку М.

При движении точки М вектор r¯ будет с течением времени изменяться и по модулю, и по направлению. Следовательно, r¯ является переменным вектором (вектором-функцией), зависящим от аргумента t:

3.Абсолютная скорость точки

Движение точки по отношению к неподвижной системе координат называ­ется абсолютным или сложным. Скорость в этом движении называют абсолютной  и обозначают    и  .

Равенство выражает теорему о сложении скоростей: абсолютная скорость точки равна геометрической сумме переносной и относительной скоро­стей.

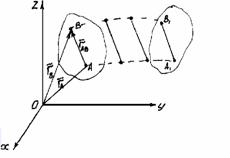
4. Скорость и ускорение точек твердого тела при поступательном движении

Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной своему начальному направлению.

При поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.

Пусть твердое тело совершает поступательное движение относительно системы отсчета OXYZ. Положение точек А и В определено радиусами-векторами   и  соответственно, а положение точки В относительно точки А - радиусом-вектором  . Тогда  , где  = const, учитывая, что   и  тогда  , но 

Следовательно | |=| | (1.62)

Взяв производные от скоростей обеих точек,   или | |=| | 

5.Формула Эйлера

6.Трансверсальная составляющая вектора скорости точки

7.Как называется и куда направлен вектор ε¯× r¯ при вращении твердого тела вокруг неподвижной оси

- вектор вращательного ускорения точки

-вектор    направлен по касательной к траектории точки в одну сторону со скоростью, если вращение ускоренное, и в противополож­ную сторону, если оно замедленное

8.Направляющие косинусы вектора ускорения точки в декартовых координатах

9. Число степеней свободы в твердом теле при плоском движении

Числом степеней свободы твердого тела называется число независимых параметров, которые однозначно определяют положение тела в пространстве относительно рассматриваемой системы отсчета. Движение твердого тела во многом зависит от числа его степеней свободы.

На плоскости твердое тело имеет три степени свободы(одну вращательную и две поступательные)

9. Поступательное движение твердого тела

Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.

Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли и т.д.