
Задача д4
Дано:





Найти:
 в момент, когда
в момент, когда

Решение


 1
1




 2
2


 3
3
 300
300




Рис.1
Применим теорему об изменении кинетической энергии системы:

Так
как система состоит из абсолютно твёрдых
тел, соединённых нерастяжимыми нитями,
то сумма работ внутренних сил системы
равна нулю:
 .
В начальном положении система находится
в покое, следовательно,
.
В начальном положении система находится
в покое, следовательно,
 .
Теперь уравнение примет вид:
.
Теперь уравнение примет вид:

Кинетическая энергия системы в конечном положении равна сумме кинетических энергий всех тел системы:
 (2)
(2)
Кинетическая энергия груза 1, движущегося поступательно:

Кинетическая энергия тела 2, вращающегося вокруг неподвижной оси:

Кинетическая энергия тела 3, совершающего плоскопараллельное движение:

Моменты инерции тел равны:

Подставив все данные в формулу (2), получим:

Выразим
входящие сюда скорости
 через скорость
груза 1.
через скорость
груза 1.
Из схемы на рис. 1 определим:

Определим положение мгновенного центра скоростей катка 3 (рисунок). Тогда


Подставим полученные выражения скоростей в равенство (3):

Найдём
сумму работ всех внешних сил, приложенных
к системе, на заданном перемещении
 груза 1.
груза 1.
Работа силы трения скольжения груза 1:

Работа силы веса катка 3:

Работа силы трения качения катка 3:

Работа силы :

Выразим
перемещения
 через перемещение
груза 1. При этом учтём, что зависимость
между перемещениями такая же, как и
между соответствующими скоростями:
через перемещение
груза 1. При этом учтём, что зависимость
между перемещениями такая же, как и
между соответствующими скоростями:



Подставим найденные перемещения в выражения работ и определим их сумму:


Подставив числовые данные, получим при :


По
теореме (2) приравняем значения T
и
 :
:

Подставим числовые данные и определим скорость груза:



Ответ:

Задача д5
Дано:



Найти:

Решение

1 2






300
3
Рис. 1. Схема механической системы
1. Выразим угловые перемещения колёс через перемещение груза :

Определим
значение силы
 ,
при котором система будет находиться
в покое. Для этого воспользуемся принципом
возможных перемещений.
,
при котором система будет находиться
в покое. Для этого воспользуемся принципом
возможных перемещений.
Сообщим
системе возможное перемещение в
направлении действия силы
 .
При этом груз 3 поднимется на величину
.
При этом груз 3 поднимется на величину
 ,
колесо 1 повернётся на угол
,
колесо 1 повернётся на угол
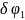 по часовой стрелке, а колесо 2 повернётся
на угол
по часовой стрелке, а колесо 2 повернётся
на угол
 против
часовой стрелки (рис.2).
против
часовой стрелки (рис.2).

 1
1




 2
2



 3
3

Ф
Рис.2
Для
неподвижной механической системы сумма
элементарных работ активных сил
 .
.
 (3)
(3)
Используя
уравнения связи (1) и (2) выразим в уравнении
(3) возможные перемещения
и
через
 :
:


Сократив на и подставив численные значения исходных данных, получим:

2. Для определения ускорения груза 3 и угловых ускорений колёс воспользуемся общим уравнением динамики

где
 сумма
элементарных работ сил инерции.
сумма
элементарных работ сил инерции.
Выберем
направление ускорения груза 3. Оно,
очевидно, будет направлено вверх,
поскольку под действием силы
колесо 2 поворачивается против часовой
стрелки. На рис.2 показаны направление
ускорения груза
и направления угловых ускорений
 .
.
Приложим к каждому телу системы главный вектор и главный момент сил инерции.
Груз
3 движется поступательно и его силы
инерции приводятся только к главному
вектору
 .
.
Колёса
1 и 2 совершают вращательное движение и
их силы инерции приводятся к главным
моментам
 и
и
 .
Здесь
.
Здесь

Составим
общее уравнение динамики, при этом
 .
.

Подставим
в это уравнение
 :
:

Используя уравнения связи (1) и (2) выразим в этом уравнении возможные перемещения и через :

Дифференцируя дважды по времени уравнения связи, выразим угловые ускорения колёс через ускорение груза :

Подставим эти соотношения в уравнение (4):

Сократив на и проделав элементарные алгебраические преобразования, получим:

Произведём вычисления:


Находим угловые ускорения колёс:


3. Для определения реакций внешних и внутренних связей воспользуемся методом кинетостатики. Система, к каждому телу которой кроме активных сил и реакций связей приложен главный вектор и главный момент сил инерции, находится в состоянии покоя и её можно рассматривать как неподвижную составную конструкцию, используя уравнения равновесия статики. Внешними связями являются подшипники и . Внутренние связи – это нить, соединяющая груз 3 с колесами 1 и 2, и точка контакта этих колёс.
Разъединим систему, показанную на рис. 2, по внутренним связям на отдельные тела и рассмотрим равновесие каждого тела.
Груз 3


Ф
Рис.3
Уравнения равновесия груза 3:
 (9)
(9)
 (10)
(10)
Из уравнения (10) находим натяжение нити:


Колесо 2



Рис.4
Уравнения равновесия:



Из
уравнения (13) находим усилие
,
при этом численно
 :
:


Из уравнения (12) находим :

Колесо 1

Рис.5
Уравнения равновесия:




Из уравнения (14) находим :

Из уравнения (15) находим :


Уравнение (16) используем для проверки правильности решения:

