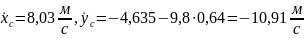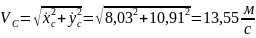Задача д1

Дано:

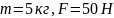
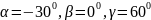
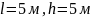
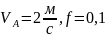
Определить: 1. Уравнения движения точки на участках АВ и ВС

2.

3.

Решение

Рассмотрим движение точки на участке в системе координат (рис.1). На точку действуют сила тяжести , сила , нормальная реакция плоскости и сила трения .

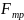Определим начальные условия движения:

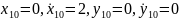
α

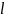
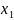
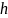
O

Рис. 1

Составим дифференциальное уравнение движения точки:

Сила трения

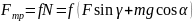
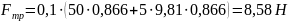
Подставляя численные значения 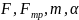в уравнение (1), получим:

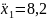(2)

Уравнение (2) представляет собой дифференциальное уравнение движения точки на участке . Его решение:

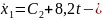уравнение скорости,

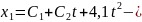уравнение движения.

Постоянные интегрирования 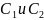найдём из начальных условий движения. При

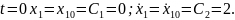
Таким образом, уравнение движения и уравнение скорости точки на участке имеют вид:

(3)

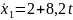(4)

Найдём время 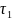движения точки на участке . При 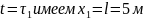и уравнение (3) принимает вид:

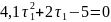
Корни полученного квадратного уравнения:

Отрицательное решение не имеет смысла и его в расчёт не принимаем. Скорость точки в положении найдём из уравнения (4), подставив в него .

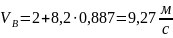
Рассмотрим движение точки на участке ВС в системе координат .

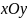Начальные условия движения:

Составим дифференциальные уравнения движения:

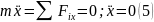
Уравнение (5) имеет решение

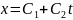
При 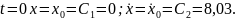Таким образом,

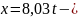уравнение движения точки относительно оси 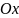, (7)

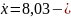уравнение скорости точки относительно оси . (8)

Уравнение (6) имеет решение

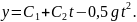
Постоянные интегрирования найдём из начальных условий движения. При Таким образом, получим:

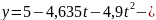уравнение движения точки, (9)

уравнение скорости точки по оси 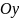. (10)

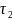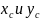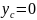Время движения точки на участке ВС и координаты точки в положении найдём из совместного решения уравнений (7) и (9), учитывая, что . При

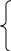
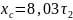
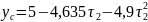
Решая эту систему уравнений, получим:

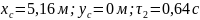
Подставив в уравнения (8) и (10), найдём скорость точки в положении :