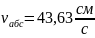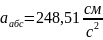Задача к3

Дано:

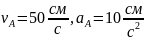
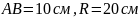
Найти:

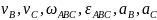
Решение

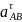
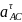
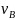
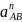
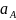
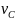
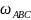
1) Определение скоростей точек и угловой скорости тела abc.

Мгновенный центр скоростей тела ABС находится в точке . По заданной скорости точки определяем угловую скорость тела:

Величины скоростей точек и :

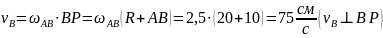
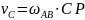
Из рисунка определяем:

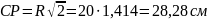
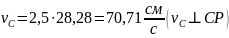
2) Определение ускорений точек и углового ускорения тела авс.

Ускорение точки определяем, используя теорему о сложении ускорений:

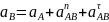(1)

Нормальное ускорение точки во вращательном движении вокруг полюса равно:

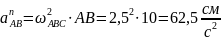
Вектор направлен от к , а вектор 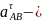перпендикулярно 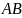в направлении углового ускорения тела. По заданному ускорению точки определяем угловое ускорение тела:

Тогда величина касательного ускорения точки во вращательном движении вокруг точки будет равна:

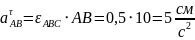
Записывая векторное равенство (1) в скалярном виде c учётом направлений векторов 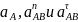, получаем:

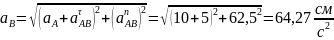
Ускорение точки определяем, используя теорему о сложении ускорений:

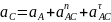(2)

Нормальное ускорение точки во вращательном движении вокруг полюса равно:

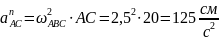
Вектор направлен от к , а вектор 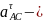перпендикулярно в направлении углового ускорения тела.

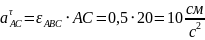
Записывая векторное равенство (2) в скалярном виде c учётом направлений векторов 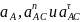, получаем:

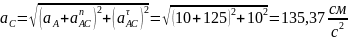
Ответ:

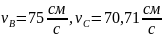
Задача к4

Дано:

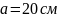
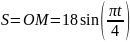
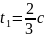
Найти: в момент времени

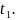
Решение

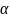
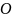
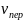
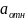
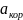
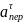
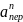
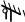
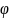
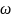
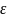
Рис.1

Рассмотрим движение точки как сложное, считая её движение вдоль пластины относительным, а вращение пластины – переносным движением. Тогда:

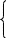
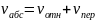(1)

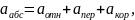(2)

где, в свою очередь,

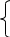
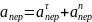(3)

(4)

Определяем характеристики относительного и переносного движений.

1) Относительное движение

Это движение происходит по закону

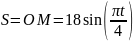
Установим, где будет находиться точка М на прямой BD в момент времени :

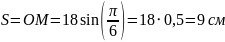
Изображаем точку М в этом положении на рисунке. Находим числовые значения :

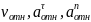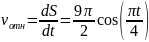
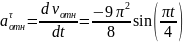
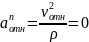
В момент времени получаем:

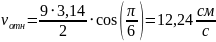
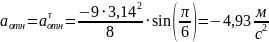
Изображаем все векторы на рисунке с учётом их направлений.

2) Переносное движение

Это движение (вращение пластины) происходит по закону

Находим угловую скорость и угловое ускорение переносного движения:

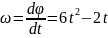
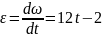
В момент времени получаем:

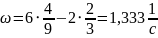
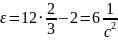
Направления и совпадают с направлением положительного отсчёта угла . Отметим это на рисунке.

Находим расстояние ОМ точки М от оси вращения. Из рисунка следует:

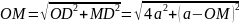
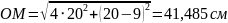
Тогда в момент получаем:

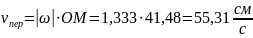
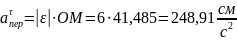
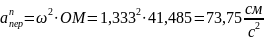
3) Кориолисово ускорение

Так как угол между вектором и осью вращения (вектором ) равен 90⁰, то численно в момент времени

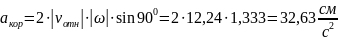
Направление вектора находим по правилу Н. Е. Жуковского. Так как вектор лежит в плоскости, перпендикулярной оси вращения, то поворачиваем его на 90⁰ в направлении (против хода часовой стрелки). Изображаем вектор на рисунке.

4) Определение

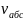
Из рисунка следует, что угол между векторами и равен 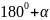, где угол определяем из рисунка:

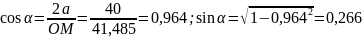
Тогда величину абсолютной скорости определяем по теореме косинусов:

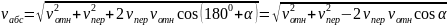
Подставляем числовые значения величин:

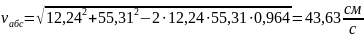
5) Определение

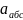
Вектор слагается из следующих векторов:

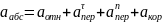
Для определения величины абсолютного ускорения спроектируем данное векторное равенство на оси (рис.1) выбранной системы координат:

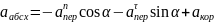
Подставив числовые данные, получаем:

Тогда величина абсолютного ускорения

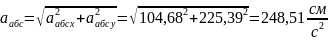
Ответ: