9. Влияние параметров нелинейного элемента и линейной части на амплитуду и частоту автоколебаний. Рекомендации по стабилизации систем

Найдем k_гр ЛЧ при котором исчезает автоколебание:

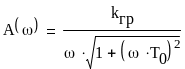
- АЧХ ЛЧ

|–Z_НЭ(А)| будет минимальным при и равен

Приравнивая |Z_НЭ(А_min)| = A(ω₀) найдем k_ГР:

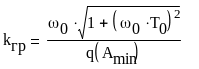
k_ГР = 0.1447

При k < k_ГР автоколебания исчезнут что видно на рис.15 (нет пересечения –Zнэ(A) и W(jω)).

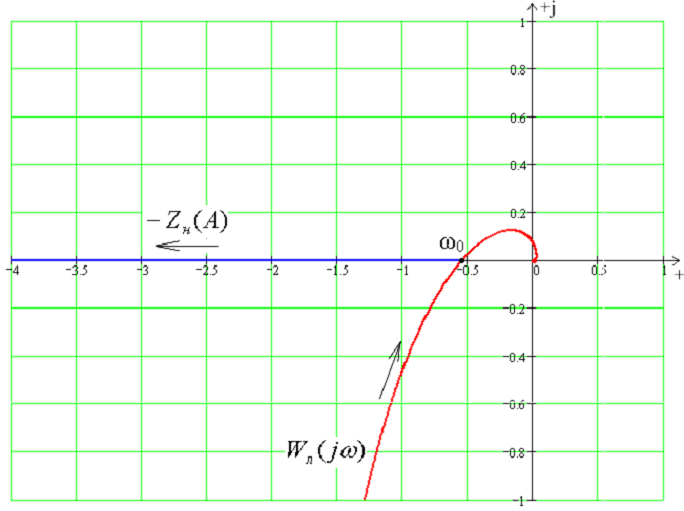
Рис 15. Графики –Zнэ(A) и W(jω) при τ = 4 с и k_ГР = 0.1447.

Найдем b_ГР при котором исчезают колебания в системе:

Для этого приравнивая |Z_НЭ(А_min)| = A(ω₀) выразим b_ГР:

.

Получим b_ГР = 248.79. При b < b_ГР колебания в системе отсутствуют, что видно на рис 16. (нет пересечения –Zнэ(A) и W(jω)).

Найдем c_ГР при котором исчезают колебания в системе:

Для этого приравнивая |Z_НЭ(А_min)| = A(ω₀) выразим c_ГР:

Получим c_ГР = 1.061. При с < c_ГР колебания в системе отсутствуют (нет пересечения –Zнэ(A) и W(jω)).

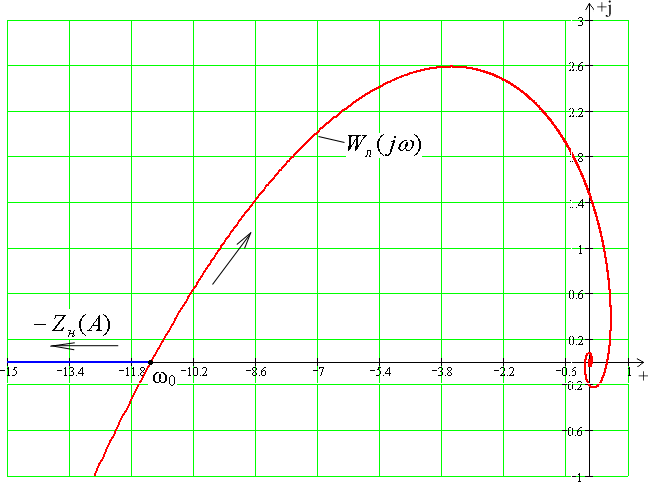
Рис 16. Графики –Zнэ(A) и W(jω) при τ = 4с и b_ГР = 248.79.

На частоту влияют только параметры ЛЧ. При увеличении T₀ частота колебаний уменьшается.

10. Построение диаграммы качества

Для построения диаграммы качества будем рассматривать колебательный переходный процесс в системе как собственные колебания системы при отсутствии внешних воздействий. Если выполнена гармоническая линеаризация нелинейного элемента, то переходный процесс мы будем искать в виде:

Будем считать переходные колебания близкими к синусоидальным, полагая, однако, что показатели затухания ξ и ω медленно изменяются с изменением амплитуды колебаний a в ходе процесса. Сама амплитуда а(t) может меняться быстро вплоть до затухания за один – два периода. Тогда решение вместо (9) надо искать в виде:

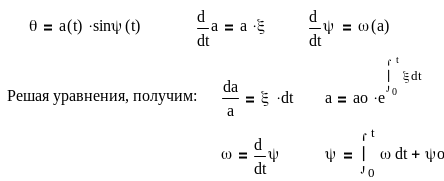
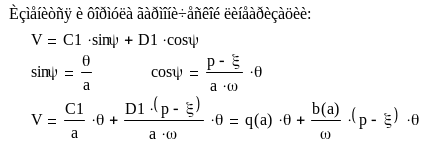
коэффициенты q(a) и b(a) вычисляются аналогично гармонической линеаризации НЭ.

Для построения диаграммы качества используем:

подставив вместо Q знаменатель передаточной функции ЛЧ, а вместо R его числитель и выделив мнимую и действительную часть получим:

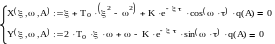
(1)

(2)

Из (1) и (2) выделим K от ξ, ω. В итоге получим:

Подставляя вместо ξ конкретные значения получим график зависимости A(K). При ω= ω_п:

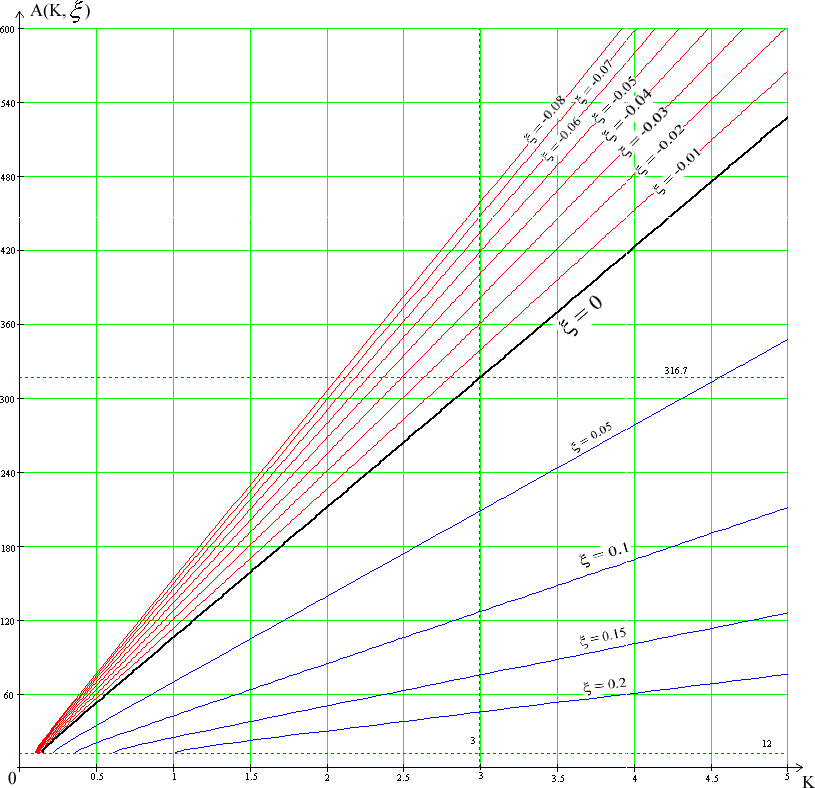
По диаграмме качества построим график зависимости ξ(а) при постоянном значении k_лч=3:

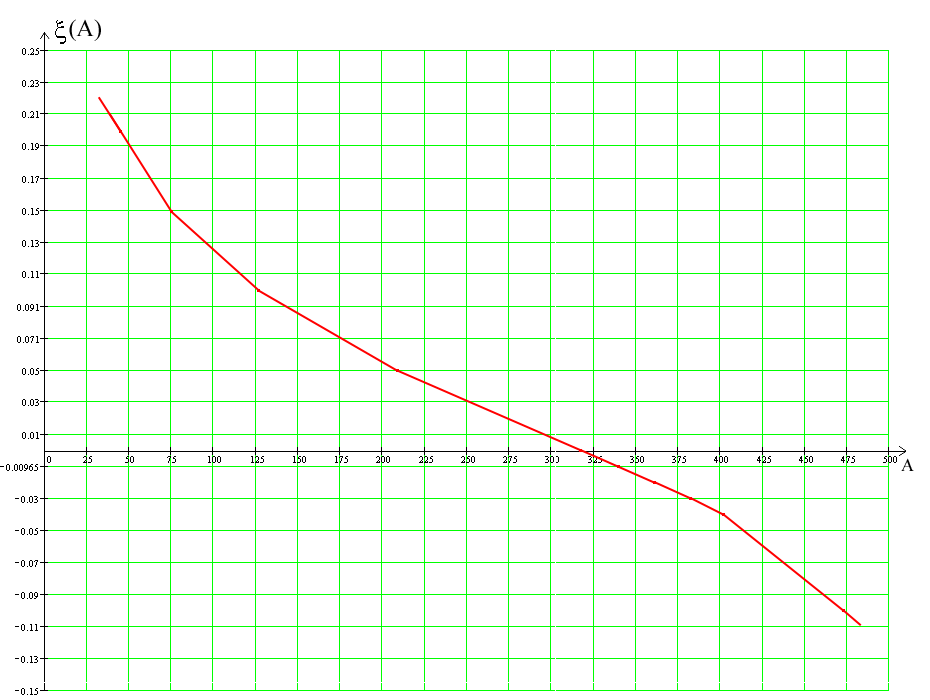
11. Заключение.

Была исследована нелинейная система автоматического регулирования температуры. Выведено дифференциальное уравнение, построены фазовые портреты системы при наличии и отсутствии запаздывания. Расчет периодического режима был проведен двумя методами: методом фазовой плоскости (точный метод) и частотным методом (приближенный метод). Определены наличие и параметры автоколебаний, т.е. амплитуда и частота периодического режима, в обоих методах. Приведены оценки влияния параметров нелинейного элемента и линейной части на параметры периодического режима.

При заданных параметрах САР температуры печи устойчива, имеет автоколебания с параметрами:

Точный метод:

A_П = 311.77

ω_П = 0,167 с^-1

Приближенный метод:

ω₀ = 0.148 с^-1

А_П = 316.69