Расчет переходного процесса ξ(t):
Для построения ξ(t) по структурной схеме сделаем преобразование:
.
Переходя во временную область:
,
если при t = 0, ξ = 0, то С1
= 0.
а) без запаздывания (при НУ , при ):
С учетом НУ на
,
получим
при
.
Время нахождения на каждом участке
равно времени нахождения на участках
для
(так
как переключение функции НЭ происходит
в одни и те же моменты времени), начало
I участок (для данных НУ).
с учетом
Время на участке
НУ для следующего участка
Время до конца участка
НУ для следующего участка
Время до конца участка
НУ для следующего участка
Время до конца участка
Далее аналогично
;
; 
;
; 
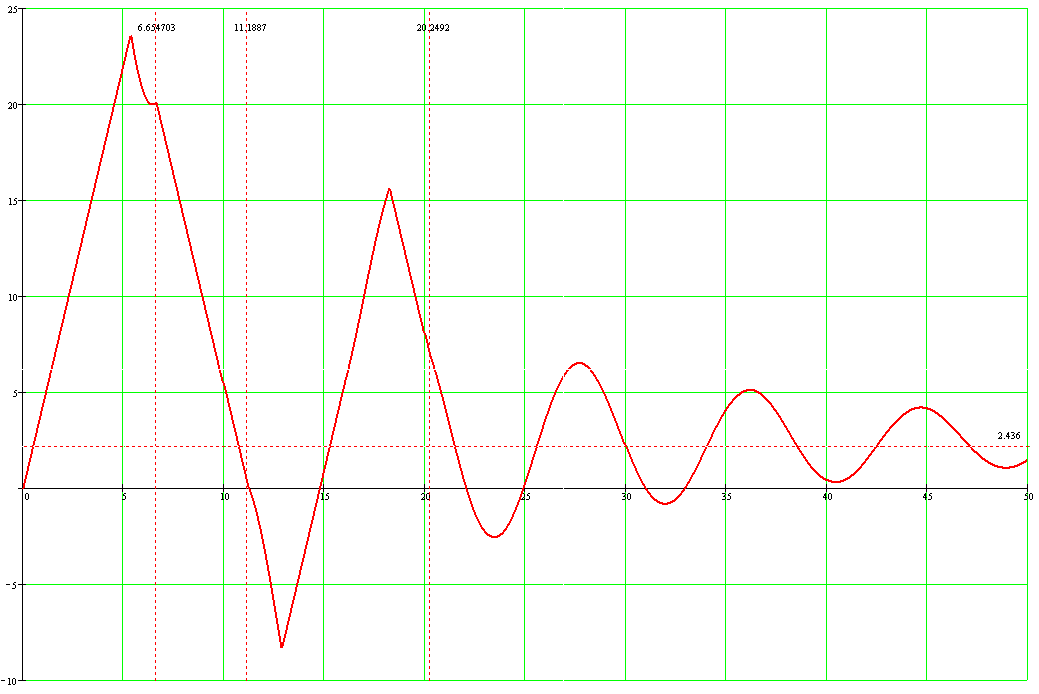
Рис 10. График переходного процесса ξ(t) без учета запаздывания.
б) с учетом запаздывания:
с учетом
Время на участке
НУ для следующего участка
Время до конца участка
НУ для следующего участка
Время до конца участка
Далее аналогично
;
;
;
; 
; 
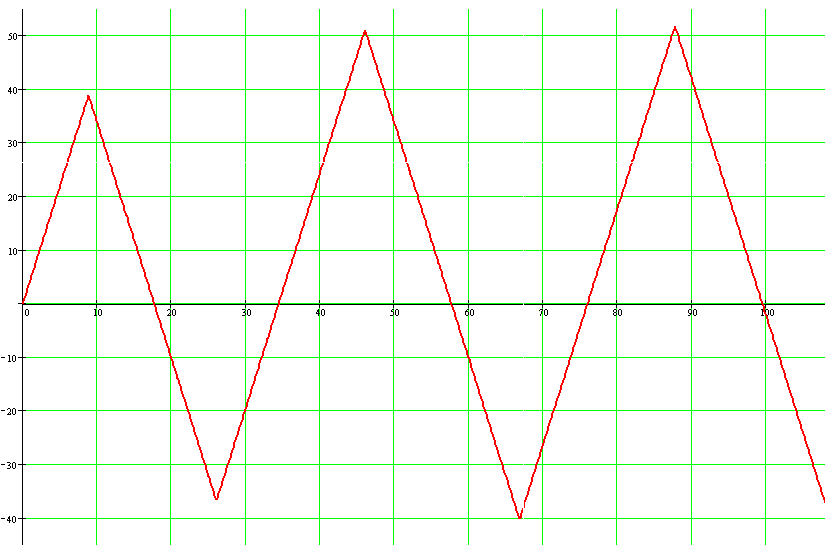
Рис 11. График переходного процесса ξ(t) с учетом запаздывания.
7. Гармоническая линеаризация нелинейного элемента, вывод Wн(а).
Метод гармонической линеаризации является приближенным методом исследования НСАР. Основу этого метода составляют следующие положения.
Пусть имеется нелинейное звено с характеристикой y = F(x). Подадим на вход этого звена гармонический сигнал x = A∙sin ωt. На выходе получим y= F(A∙sin ωt). Этот периодический выходной сигнал можно разложить в ряд Фурье.
Предположим, что наша система обладает тем свойством, что величина амплитудной характеристики на частотах высших гармоник значительно меньше, чем для первой: |Wл(jnω)| << |Wл(jω)|, где n = 2, 3, …
Это свойство называется свойством фильтра линейной части системы. Значит, в силу резонансных и фильтрующих свойств линейной части, на выходе НЭ для расчета периодических режимов можно учитывать только основную, первую гармонику, получим x = A∙sin ωt.
Проведем гармоническую линеаризацию нелинейного элемента для нашего случая:
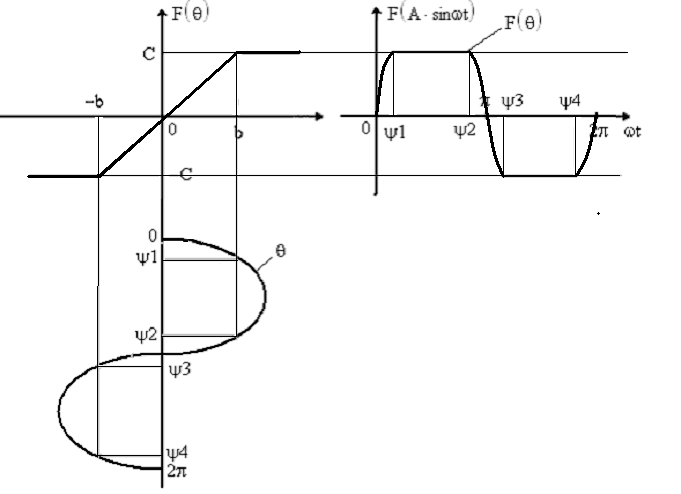
Рис 12. Преобразование НЭ
Найдем q(A) и b(A):
В силу симметрии функций sin и НЭ
относительно центра координат будем
рассматривать интеграл на четверти
периода (от 0 до
)
На участке
F(Asinψ)=
На участке
F(Asinψ)= с
b(A) = 0, т.к. нелинейность однозначна. При гармоническом воздействии основная гармоника выходных колебаний НЭ с однозначными характеристиками совпадают по фазе с входной величиной.
8. Расчет знсау частотно-амплитудным методом с запаздыванием и без него. Определение параметров автоколебания и оценка их устойчивости.
Условие возникновения ПР запишется,
как
или
Для того, чтобы обнаружить есть или нет
ПР в ЗГЛНС необходимо построить в единых
координатах АФХ ЛЧ
и инверсную АФХ НЭ с обратным знаком
.
Рассчитаем систему без запаздывания, т.е. при τ = 0 с:
Для этого найдем частоту ω0 при котором ФЧХ ЛЧ будет равна –π
– ФЧХ ЛЧ
Это уравнение не имеет корней, а, следовательно, нет периодического режима в системе. Это можно видеть на рисунке.
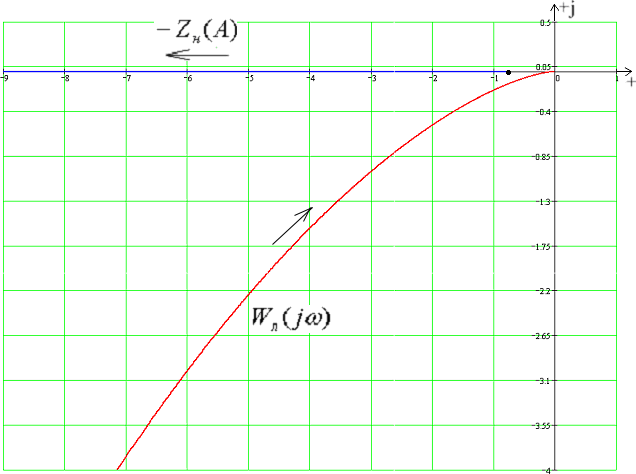
Рис 13. АФХ ЛЧ и инверсная АФХ НЭ при τ = 0 с.
Рассчитаем систему при τ = 4 с:
Для этого найдем частоту ω0 при котором ФЧХ ЛЧ будет равна –π
– ФЧХ ЛЧ
Решением данного уравнения будет частота ω0 = 0.14831 с-1
Приравняем ZНЭ(AП) = A(ω0) и найдем АП,
где – АЧХ ЛЧ
решением будет АП =316.69, т.е. есть точка пересечения АФХ линейной части и –ZНЭ.
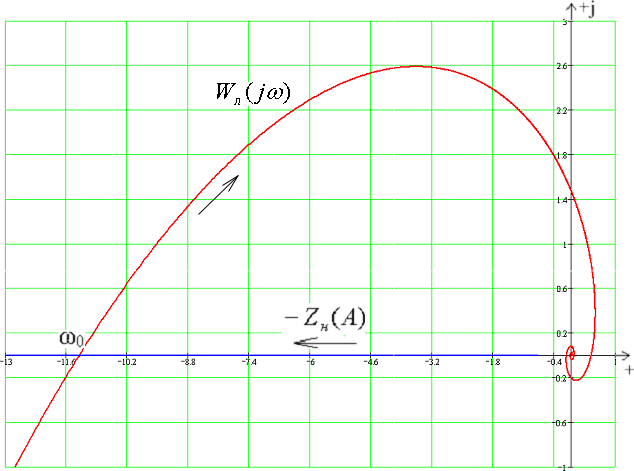
Рис 14. Пересечения АФХ ЛЧ и инверсной АФХ НЭ при τ = 4 с.
В системе есть периодический режим с параметрами:
ω0 = 0.14831 с-1
АП = 316.69
По рисунку видно, что –ZНЭ пересекает АФХ изнутри наружу, т.е. периодический режим в системе устойчивый.