Расчет переходного процесса :

Исходя из начальных условий, определяют постоянные интегрирования на каждом участке, находят время движения по каждому участку, вычисляют значения и .

1), , без учета запаздывания

Первый участок первого круга.

а). Дифференциальное уравнение для первого участка имеет вид

. (1)

Пусть . (2)

Тогда уравнение (1) примет вид

. ( )

Решением уравнения ( ) будет

. (3)

Следовательно, решение уравнения (2) примет вид

(4)

(3) и (4) – решения уравнения динамики для первого участка.

б). Определяем постоянные интегрирования c₁ и с₂. для первого участка, т.е.

, при t = t ₁= 0 с . Из (3) при t=0 имеем:

, (5)

.

Из уравнения (4) получаем:

, (6)

.

в). Находим время движения по первому участку - t₁.

В конце первого участка .

Из уравнения (4) имеем: , (7)

Решая последнее уравнение, находим t₁. Все вычисления в основном производим с помощью математического пакета «Mathcad». Из него видно, что имеет два решения. Учитывая то, что время должно иметь положительное вещественное значение, получаем t₁=5,377 с.

г). Определим координаты и в конце первого участка. Первая координата известна и имеет значение , вторую находим из (3), при t = t₁ = 5,377 с:

, (8)

.

Второй участок первого круга.

а). Дифференциальное уравнение для второго участка имеет вид

. (9)

Введем обозначение (2) и получаем систему дифференциальных уравнений:

(10)

Решение второго дифференциального уравнения системы (11) имеет вид

(11)

(12)

где и - действительная и мнимая часть комплексных корней решения характеристического уравнения.

б). Определим постоянные интегрирования с₃ и с₄ из начальных условий для второго участка. Координаты в начале второго участка равны координатам в конце первого участка, т.е.

, при t = t ₂= 0с.

Из уравнения (11):

Из уравнения (12):

в). Находим время движения по второму участку t₂.

В конце второго участка . Из уравнения (11) находим t₂:

(13)

с - время движения по второму участку

г). Определим координаты и в конце второго участка.

Первая координата известна и имеет значение , вторую находим из (12) при t=t₂=1,277с:

, (14)

.

Третий участок первого круга

а). Дифференциальное уравнение для третьего участка имеет вид

. (15)

Применив (2) уравнение (15) перепишем

.

Решением уравнения будет

. (16)

Следовательно, решение уравнения (2) в этом случае примет вид

. (17)

(16) и (17) – решения уравнения динамики для третьего участка.

б). Определяем постоянные интегрирования c₅ и с₆. из начальных условий для третьего участка. Координаты в начале третьего участка равны координатам в конце второго участка, т.е. , при t = t₃ = 0 с. Из уравнения (16) имеем:

, (18)

.

Из уравнения (17) получаем

, (19)

.

в). Находим время движения по третьему участку t₃.

В конце третьего участка .

Из уравнения (17) имеем:

, (20)

Решая последнее уравнение, находим t₃ =4,534с.

г). Определим координаты и в конце третьего участка.

Первая координата известна и имеет значение , вторую координату находим из (16 при t₃=4,534с:

, (21)

.

Далее, для каждого участка (в порядке очередности) таким же образом находим: постоянные интегрирования, время движения по участку, координаты и в конце участка.

Четвертый участок первого круга.

Время движения по второму участку t₂.

Координаты и в конце второго участка при .

Первый участок второго круга

Время движения по первому участку t₁.

Координаты и в конце первого участка при .

Второй участок второго круга.

Время движения по второму участку t₂.

Координаты и в конце второго участка при .

Третий участок второго круга

Время движения по третьему участку t₃.

Координаты и в конце третьего участка при .

Четвертый участок второго круга.

Время движения по второму участку t₂.

Координаты и в конце второго участка при

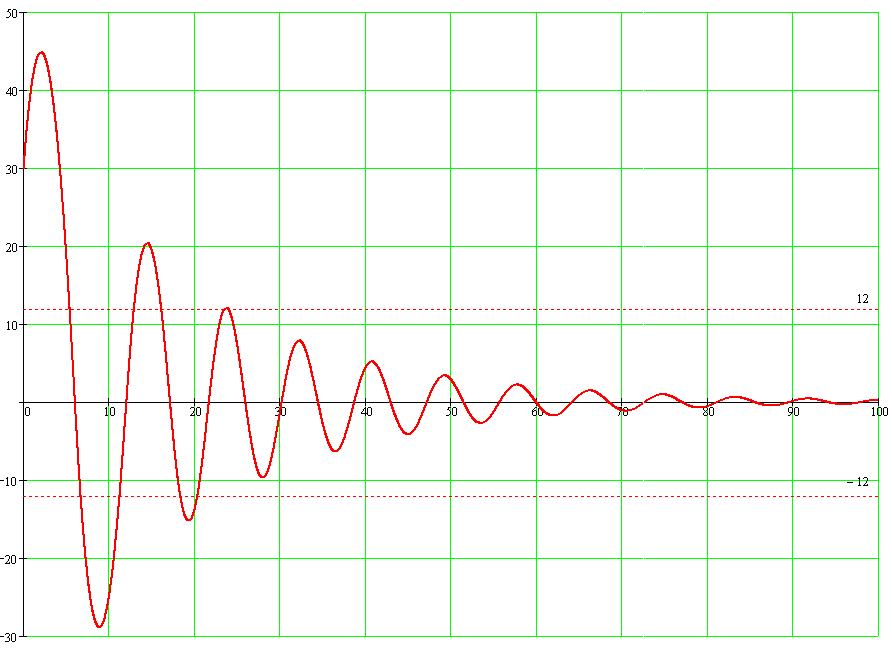
Рис 8. График переходного процесса без учета запаздывания.

2) , с учетом запаздывания

Первый участок первого круга.

а). Дифференциальное уравнение для первого участка имеет вид

. (1)

Пусть . (2)

Тогда уравнение (1) примет вид

. ( )

Решением уравнения ( ) будет

. (3)

Следовательно, решение уравнения (2) примет вид

(4)

(3) и (4) – решения уравнения динамики для первого участка.

б). Определяем постоянные интегрирования c₁ и с₂. для первого участка, т.е.

, при t = t₁ = 0с . Из (3) при t=0 имеем:

, (5)

.

Из уравнения (4)получаем

, (6)

.

в). Находим время движения по первому участку t₁.

В конце первого участка .

Из уравнения (4) имеем:

, (7)

Решая последнее уравнение, находим t₁. Все вычисления в основном производим с помощью математического пакета «Mathcad 2000». Получаем t₁=4,68с.

Учитывая запаздывание, получим t₁=8,68с

г). Определим координаты и в конце первого участка. Находим из (3) и (4), при t=t₁=8,68с:

, (8)

.

Второй участок первого круга.

а). Дифференциальное уравнение для второго участка имеет вид

. (9)

Введем обозначение (2) и получаем систему дифференциальных уравнений:

(10)

Решение второго дифференциального уравнения системы (10) имеет вид

(11)

(12)

где и - действительная и мнимая часть комплексных корней решения характеристического уравнения.

б). Определим постоянные интегрирования с₃ и с₄ из начальных условий для второго участка. Координаты в начале второго участка равны координатам в конце первого участка, т.е. , при t=t₂=0с.

Из уравнения (13): (13)

Из уравнения (12): (14)

в). Находим время до конца второго участка - t₂.

В конце второго участка . Из уравнения (12) находим t₂:

(15)

с

Учитывая запаздывание, получим t₂=8,8с

г). Определим координаты и в конце второго участка.

Находим из (11) и (12) при t=t₂=8,8с:

.

Третий участок первого круга

а). Дифференциальное уравнение для третьего участка имеет вид

. (17)

Применив (2) уравнение (17) перепишем

.

Решением уравнения будет

. (18)

Следовательно, решение уравнения (2) в этом случае примет вид

. (19)

(18) и (19) – решения уравнения динамики для третьего участка.

б). Определяем постоянные интегрирования c₅ и с₆. из начальных условий для третьего участка. Координаты в начале третьего участка равны координатам в конце второго участка, т.е. , при t=t₃=0 с. Из уравнения (18) имеем:

, (20)

.

Из уравнения (19) получаем

, (21)

.

в). Находим время до конца третьего участка - t₃.

В конце третьего участка .

Из уравнения (19) имеем:

, (22)

Решая последнее уравнение, находим t =22,03с. Учитывая запаздывание, получим t₃=26,03с

г). Определим координаты и в конце третьего участка.

Находим из (18) и (19) при t₃ =26,03с:

.

Далее, для каждого участка (в порядке очередности) таким же образом находим: постоянные интегрирования, время движения по участку, координаты и в конце участка.

Четвертый участок первого круга.

Время движения до конца второго участка с учетом запаздывания - t₂.

Координаты и в конце второго участка при .

Первый участок второго круга

Время движения до конца первого участка с учетом запаздывания - t₁.

Координаты и в конце первого участка при .

Второй участок второго круга.

Время движения до конца второго участка с учетом запаздывания - t₂.

Координаты и в конце второго участка при .

Третий участок второго круга

Время движения до конца третьего участка с учетом запаздывания - t₃.

Координаты и в конце третьего участка при .

Четвертый участок второго круга.

Время движения до конца второго участка с учетом запаздывания - t₂.

Координаты и в конце второго участка при

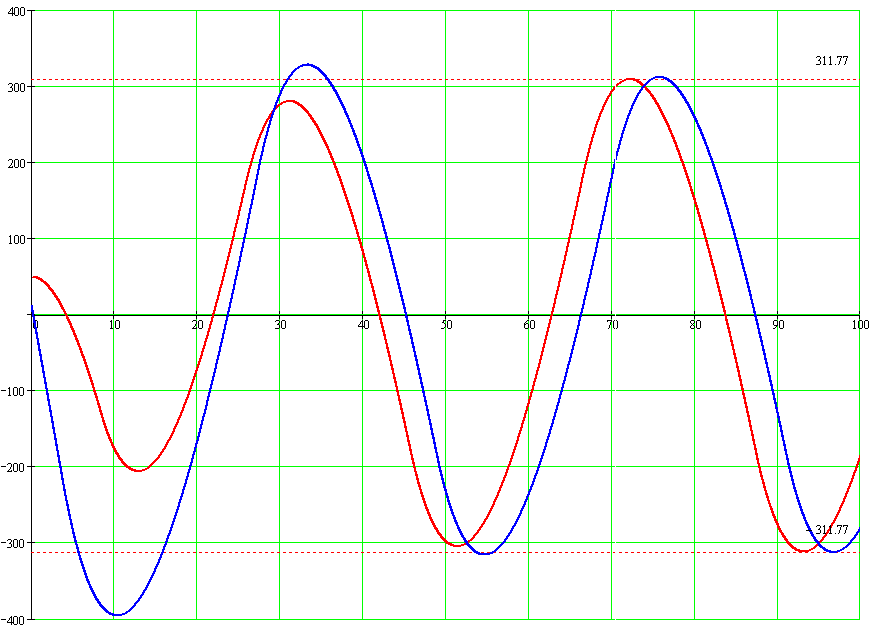
Рис 9. График переходного процесса с учетом запаздывания.