Оценка коэффициентов корреляции и регрессии

при r < 0,4 и n > 30

Средняя квадратическая погрешность оценки r при данном значении п и в этом, случае производится по формуле

σ _r (1.22)

средняя квадратическая погрешность коэффициента регрессии а рассчитывается по формуле

(1.23)

коэффициента b — по формуле

(1.24)

С учетом того, что распределение оценки коэффициента корреляции при указанных условиях имеет нормальный характер, можно определить (см. гл. 6) доверительные интервалы коэффици­ентов корреляции и регрессии при заданном уровне значимости:

; (1.25)

; (1.26)

; (1.27)

Нередко в исследованиях возникает вопрос о реальности связей вообще, т. е. вопрос о том, являются ли полученные по данным наблюдений коэффициенты корреляции значимыми и не объясняются ли они случайностями выборки.

Обычно он решается с помощью нулевой гипотезы относительно рассматриваемой связи. Например, задается нулевая гипотеза

H_о:r = 0.

Оценка гипотезы проводится по эмпирическому коэффициенту корреляции r. Для этого с учетом соотношения (1.25) строится критическая область вида

(1.28)

с уровнем значимости α. Если полученное выборочное значение r окажется в критической области, то гипотеза отбрасывается.

Оценка коэффициента корреляции при r > 0,4.

Преобразование Фишера

Как отмечалось выше, при r> 0,4 для оценки действительного значения коэффициента корреляции ввиду асимметричного рас­пределения нельзя воспользоваться формулой средней квадратической погрешности коэффициента корреляции (1.22). Поэтому для оценки г принимается преобразование Фишера, при котором коэффициент корреляции выборочных совокупностей приравнива­ется к гиперболическому тангенсу некоторого значения z

r=thz (1.31 )

Отсюда

Z= 0,5 ln[(1+r)/ (1-r)] ( 1.32)

Распределение z почти не зависит от п и r и с возрастанием п быстро приближается к нормальному закону со средним значением

(1.33)

и дисперсией

(1.34)

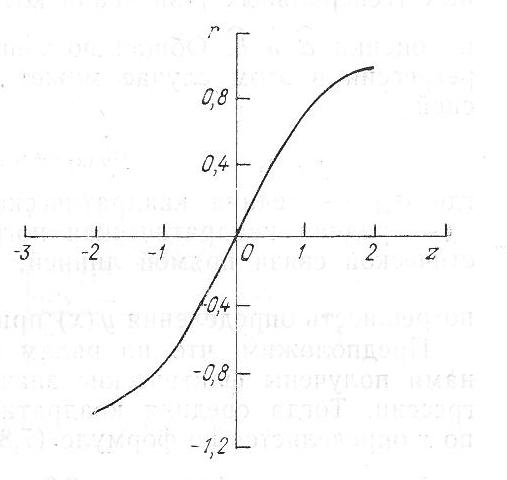
Рис. 1.7. Соотношение между коэффициентом корреляции r и преобразованием Фишера z.

Как следует из формулы (1.34), погрешность оценки z не зависит от .

Распределения для значений r = 0; 0,4; 0,8 представлены для сравнения на том же рисунке, где даны распределения выборочных коэффи­циентов корреляции (см. рис. 1.6).

При помощи статистики z можно выяснить, существенно ли отличается рассчитанное значение от предполагаемого и найти доверительные границы для действительного значения r.

Для этого необходимо по r и определить z и . Тогда ввиду нормального распределения статистики z легко решить, будет ли разность r— существенной или несущественной.

При ручном счете переход от r к z и обратно достаточно сло­жен. Поэтому он совершается обычно по таблицам или по графикам связи r=f(z) и z=f(r) (рис. 1.1). При расчете на ЭВМ определение z no r или r по z производится непосредственно по формулам (1.31), (1.32),. которые включаются в алгоритм программы.