
- •1.1.2. Функциональные и стохастические связи
- •1.1.3. Различные виды взаимосвязи природных процессов
- •1.2.2. Коэффициент корреляции
- •1.2.3. Оценка коэффициента корреляции и уравнения регрессии. Преобразование Фишера
- •Оценка коэффициентов корреляции и регрессии
- •Преобразование Фишера
- •Анализ погрешностей расчетов по уравнению регрессии
- •1.2.4. Граничные условия математической модели парной корреляции
Лекция 1. СТАТИСТИЧЕСКИЕ ЗАВИСИМОСТИ И ЛИНЕЙНАЯ
КОРРЕЛЯЦИЯ В ГЕОЭКОЛОГИИ
1.1. ВЗАИМОСВЯЗИ ЯВЛЕНИИ В ПРИРОДЕ
1.1.1. Задачи изучения взаимосвязей природных процессов
Большинство природных процессов формируется цепью причинно-следственных явлений, изменяющихся во времени и пространстве. Для изучения этих процессов необходимо установить их причины, движущие силы или источники и тенденцию развития. Например, при расчетах и прогнозах стока требуется исследовать связи колебаний водности реки с колебаниями слоя дождевых и снеговых осадков, температуры воздуха, испарения с поверхности суши и водоемов, запасов воды в снежном покрове и т.д.
Задачи изучения взаимосвязей можно условно разделить на два класса:
задачи, связанные с выяснением причин или факторов развития процессов во времени и пространстве.
задачи, связанные с определением конкретных значений или тенденции развития данного процесса в будущем. Или, иначе, решение задачи прогноза или предсказания будущих значений исследуемых явлений и восстановление пропущенных данных.
1.1.2. Функциональные и стохастические связи
Функционально зависимые величины.
Случайная величина Y называется функционально зависимой от случайной величины X, если зная значения одного из процессов, можно указать точные значения другого.

Рис. 1.1. График связи функционально зависимых величин.
![]() (1.1)
(1.1)
P=P0 + γh (1.2)
2. Независимые величины
Случайная величина Y называется независимой от случайной величины X, если закон распределения Y не зависит от того, какое значение приняло X, т. е. при любом х плотность распределения
f (y/x) = f(y) (1.3)

Рис. 1.2. График связи независимых величин.
В более общем виде распределения:
F(y, x) = F1 (y) F2 (x) (1.4)
Вероятностная (стохастическая) зависимость.
Случайная величина Y называется стохастически связанной со случайной величиной X, если зная значения одного из процессов, можно указать возможный интервал значений Y
f(x,y) = f1(x)f2(y/x) (1.5)
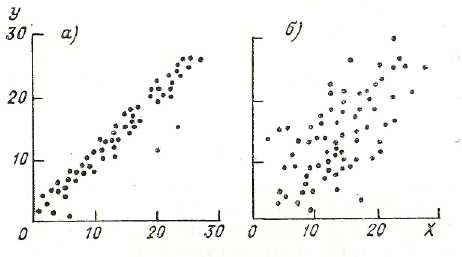
Рис. 1.3. График связи стохастически зависимых величин.
а — сильная связь, б — слабая связь.
Стохастическая связь между двумя процессами появляется обычно тогда, когда наряду с другими имеются общие факторы, влияющие как на первый, так и на второй процесс.
X= f (z1, z2,…, zm; u1, u2, … , uk)
Y= f (z1, z2,…, zm; v1, v2, … , vk)
то, очевидно, за счет общей составляющей Z между X и Y появляется взаимосвязь, причем тем более тесная, чем больше влияние Z на X и Y.
1.1.3. Различные виды взаимосвязи природных процессов
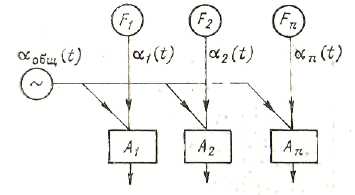
Q1 (t) Q2 (t) Qn (t)
Рис. 1.4. Схема взаимосвязи стока системы речных бассейнов.
Причинно-следственные связи – связи когда Х является причиной изменения У.
Например, на рис.1.4 это связи Qi (t) =f(αобщ (t)) и Qi (t) =f(αi (t)).
Связи сопряженности – связи разных следствий общих причин.
Например, на рис.1.4 это связи Qi (t) =f(Qj (t).
1.2. РЕГРЕССИОННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
ВЗАИМОСВЯЗИ ДВУХ ПЕРЕМЕННЫХ ВЕЛИЧИН
[ПАРНАЯ КОРРЕЛЯЦИЯ]
Линейное уравнение регрессии двух переменных величин.
Первой задачей при построении регрессионной математической модели взаимосвязи двух переменных величин является определение ыормы связи. При этом линейное уравнение регрессии двух стохастически связанных переменных величин основывается на уравнении прямой линии
Y= aX+b, (1.6)
которая проводится в поле точек стохастической связи. Но если при функциональной связи каждому значению X соответствует только одно значение Y, то при стохастической связи каждому значению X соответствует определенное множество значений Y. Поэтому значения Y, определенные по этой линии , описываются уравнением,
_
Y(X)= аX+b (1.7)
-
где в отличие от уравнения (1.6) Y(X)описывает одно из возможных значений Y при данном Х, найденное исходя из того или иного принципа, например, принципа наименьших квадратов (см. ниже). Действительное значение Y в этом случае будет
yi=
![]() (xi
) +
Si
=
axi
+
b+
Si,
(1.8)
(xi
) +
Si
=
axi
+
b+
Si,
(1.8)
где Si отклонение действительного значения Yот линии связи (1.6).
Для определения параметров а и b используем принцип наименьших квадратов (см. гл. 1), заключающийся в определении таких значений а и b, при которых среднее значение квадратов разностей фактических и рассчитанных величин So является минимальным. В результате получаем
|
|
(1.10) |
|
|
(1.11) |
|
|
(1.12) |
Найдем теперь параметры уравнения зависимости X от Y получаем
|
|
(1.14) |
и уравнение регрессии x = f(y) имеет вид
|
|
(1.15) |




