Расчет параметров показательной парной регрессии
Поскольку показательная функция относится к классу нелинейных по оцениваемым параметрам, то построению функции парной показательной регрессии
ŷ x = a·bx
предшествует, как и в случае степенной функции регрессии, процедура линеаризации переменных с помощью логарифмирования обеих частей функции регрессии. После логарифмирования получим выражение:
lg ŷ =lga + x lgb.
Для определения параметров все вычисления, как и ранее, сведем в таблицу 2.3.
При этом в таблице приведены переменные
Ŷ = lg ŷ, C = lga, B = lgb.
Тогда получим линейное уравнение регрессии в новых переменных
Ŷ = С + B x.
C учетом табличных данных значения параметров линейной регрессии составят:
B=(
-
)/
Sx2
=
(21612,2138–
3,8614*5379,5625)/
4801346,9961=0,00017;
C
=
- B
= 3,8614–
0,00017*5379,5625=2,9210.
Таким образом, получено уравнение
Ŷ = 2,9210+ 0,0002x
или после потенцирования
ŷx = 102,9210 10 0,00017x = 833,6812 (1,0004) x.
Таблица 2.3
№ |
|
|
|
|
|
|
|
|
1 |
10147 |
4,3150 |
43784,1340 |
102961609 |
18,6191 |
49528,2075 |
-28875,21 |
833777610,4627 |
2 |
9177 |
4,5918 |
42138,6329 |
84217329 |
21,0843 |
33518,4713 |
5544,53 |
30741798,1731 |
3 |
7167 |
4,1519 |
29756,8191 |
51365889 |
17,2384 |
14924,8678 |
-736,87 |
542974,1983 |
4 |
6499 |
3,9688 |
25793,2943 |
42237001 |
15,7515 |
11406,0573 |
-2099,06 |
4406041,6018 |
5 |
6061 |
4,0984 |
24840,6209 |
36735721 |
16,7972 |
9562,4141 |
2981,59 |
8889854,4568 |
6 |
6031 |
3,6133 |
21791,8917 |
36372961 |
13,0560 |
9447,6362 |
-5342,64 |
28543761,9746 |
7 |
6004 |
3,9764 |
23874,5559 |
36048016 |
15,8121 |
9345,5145 |
126,49 |
15998,5691 |
8 |
5474 |
4,1223 |
22565,3685 |
29964676 |
16,9932 |
7550,0954 |
5701,90 |
32511716,1621 |
9 |
4846 |
4,0091 |
19428,1510 |
23483716 |
16,0730 |
5863,6766 |
4348,32 |
18907916,8087 |
10 |
4807 |
3,8542 |
18527,3571 |
23107249 |
14,8552 |
5772,3454 |
1376,65 |
1895177,9935 |
11 |
4308 |
4,0182 |
17310,4100 |
18558864 |
16,1459 |
4721,9428 |
5706,06 |
32559088,4425 |
12 |
4203 |
3,6773 |
15455,8312 |
17665209 |
13,5228 |
4526,5298 |
230,47 |
53116,5246 |
13 |
3824 |
3,8132 |
14581,6024 |
14622976 |
14,5403 |
3886,0764 |
2617,92 |
6853524,0152 |
14 |
3407 |
3,6577 |
12461,8689 |
11607649 |
13,3790 |
3285,5978 |
1261,40 |
1591135,4944 |
15 |
3161 |
3,5499 |
11221,1112 |
9991921 |
12,6015 |
2975,8460 |
571,15 |
326216,8872 |
16 |
957 |
2,3655 |
2263,7720 |
915849 |
5,5955 |
1225,5275 |
-993,53 |
987096,8994 |
17 |
- |
- |
- |
- |
- |
- |
- |
- |
Сумма |
86073 |
61,7831 |
345795,4211 |
539856635 |
242,0650 |
177540,8065 |
-7580,81 |
1002603028,6640 |
Ср. знач. |
5379,5625 |
3,8614 |
21612,2138 |
33741039,6875 |
15,1291 |
- |
- |
62662689,2915 |
Sx2 , SY2 |
4801346,9961 |
0,2183 |
- |
- |
- |
- |
- |
- |
Sx, SY |
2191,1976 |
0,4672 |
- |
- |
- |
- |
- |
- |
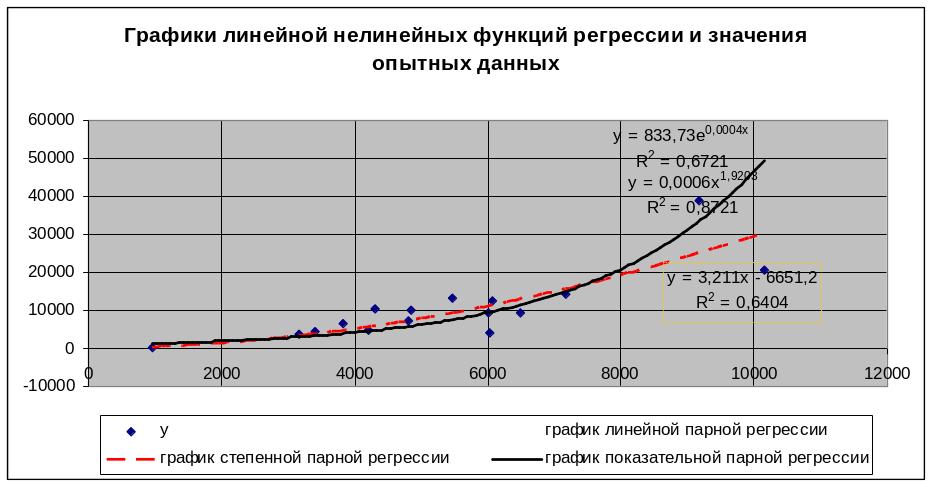
На рисунке приведены графики функций регрессии и значения опытных данных.
