2.Вывод уравнений обобщенных сил

1. Общие положения

Звенья роботов, их механические передачи и электрические двигатели представляют собой систему материальных тел, связанных между собой жесткими и упругими связями. Понятие статического и динамического режимов, которые обычно применяют для одномассового приведенного звена, для 2-х координатного электропривода неприемлемы. Здесь все режимы динамические, в большей мере обусловлены взаимным влиянием звеньев и электроприводов друг на друга.

Решение этой задачи удобно вести при использовании дифференциальных уравнений движения системы в обобщенных координатах, или при использовании уравнений Лагранжа 2-го рода.

, ( 2.1)

где – порядковый номер звена ПР;

, – обобщенная координата и обобщенная скорость i -го звена;

- обобщенная сила или момент сил, приложенных к i -му звену;

– суммарная кинетическая энергия манипулятора;

– суммарная потенциальная энергия манипулятора.

Количество управлений равно количеству звеньев. В результате решения уравнений получают выражение обобщенных сил как функции от , , , , .

2.2. Расчет кинетической энергии груза .

Кинетическая энергия груза определяется по формуле:

; ( 2.2 )

Если представить груз материальной точкой, расположенной в точке О₃ (рис.1.3), то его координаты на плоскости х-у определяются системой двух уравнений:

( 2.3)

Продифференцируем систему уравнений по времени, чтобы определить проекции скорости груза на оси координат:

Скорость груза можно определить по формуле:

Кинетическая энергия груза может быть определена по формуле:

2.3. Расчет кинетической энергии локтя.

Локоть будем рассматривать как однородный стержень длиной , с площадью поперечного сечения и плотностью материала

Выберем точку массой dm₂ , находящейся на расстоянии от , тогда ее координаты будут определяться системой уравнений и длиной ₂

Проекции скорости элемента локтя массой dm на оси х и у

Скорость элемента локтя массой dm определяется формулой:

Кинетическая энергия элемента локтя массой dm₂, которая расположена на расстоянии от точки О₂

Элемент массой локтя можно представить в виде:

,

где – усреднённая плотность материала локтя ПР,

– усреднённая площадь поперечного сечения локтя

– длина элемента массы

Кинетическую энергию локтя получим в результате интегрирования локтя по его длине

Поскольку ось О₂ проходит через конец локтя, то . С учетом этого получим:

,

4. Расчет кинетической энергии плеча манипулятора.

Плечо манипулятора будем рассчитывать как однородный стержень сечением и . Выберем материальную точку длиной и массой расположенную на расстоянии от , тогда получим координаты элемента плеча манипулятора на оси х и у:

;

Проекции скорости элемента плеча манипулятора на оси х и у:

;

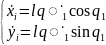Скорость элемента плеча манипулятора:

,

Кинетическая энергия элемента манипулятора:

,

Кинетическая энергия плеча манипулятора определяем в результате интегрирования по длине плеча от - до +

;

Поскольку ось поворота плеча О₁ проходит через его конечную точку, то . С учетом этого получаем:

;

2.5.Расчет кинетической энергии двигателя локотя

Двигатель Д2 приводит в движение локоть и расположен в точке Координаты двигателя на оси х и у:

;

Проекции вектора скорости двигателя локтя на оси х и у:

;

Скорость двигателя локтя:

= ;

Кинетическая энергия двигателя локтя:

;

Поскольку двигатель плеча расположен в точке О₁, и не перемещается, то его кинетическая энергия равна нулю.

2.6.Расчет потенциальной энергии груза.

Потенциальная энергия груза рассчитывается по формуле:

, (2.5)

где (2.6 )

После подставки получим:

(2.7)

2.7. Расчет потенциальной энергии локтя.

Выберем точку массой , находящуюся на расстоянии от точки , тогда по аналогии с грузом получим:

где

- плотность материала локтя;

- площадь поперечного сечения локтя.

;

;

где примем равным нулю.

2.8. Расчет потенциальной энергии плеча.

Выберем точку массы , находящуюся на расстоянии от точки , тогда получим:

;

Где ;

;

где примем равным нулю.

2.9 Расчет потенциальной энергии двигателя локтя

Двигатель локтя расположен в точке

;

.

2.10 Уравнения обобщённых сил

Суммарная кинетическая энергия манипулятора:

;

Суммарная потенциальная энергия манипулятора:

.

Применительно к двухзвенному ПР получаем два уравнения обобщенных сил:

;

;

;

;

;

;

;

;

; (2.8)

. (2.9)

Выводы