Позиционные системы счисления

В ней значение цифры определяется ее местоположение в изображении числа. Упорядоченный набор символов A₀, A₁… A_n, используемые для представления любых чисел, называют ее алфавитом, а число символов алфавита p=n+1 – основание системы счисления (p-ичная система). Основание позиционной системы – количество различных чисел, используемых для отображения чисел. Наиболее употребляемая – десятичная. При записи числа в позиционной системе счисления целая часть от дробной отделяется точкой или запятой и является началом отсчета. За основание системы счисления можно принять любое натуральное число и при P>10 используются латинские буквы.

Запись любого числа в позиционной системе счисления выглядит так:

A_p=a_npⁿ+a_n-1p^n-1+…+a_o+a_-1p^-1+…a_-mp^-m

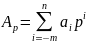
m, n – число целых и дробных разрядов. Изображение любого числа А в p-ичной системе счисления является последовательность цифр а_i.

Отсюда видно, что с уменьшением основания системы счисления уменьшается число используемых цифр, но возрастает кол-во разрядов

35=3₁₀5₁₀=2В₁₂=43₈=1₂00011₂

Арифметические действия над цифрами в любой позиционной системе счисления производятся по одним и тем же правилам. При этом только нужно пользоваться соответствующими для этих систем таблицами сложения и умножения. В любой позиционной системе счисления с любым основанием p умножение на число p^m (m - целое) сводится к переносу запятой умножаемого на m разрядов вправо или влево в зависимости от знака m. Например:

111*2¹=1110 7*2=14

Системы счисления используют для построения на их основе различных кодов для передачи, хранения и преобразования информации.

Код – система условных знаков или символов для представления различной информации. Любому дискретному сообщению можно приписать какой-либо порядковый номер. Измерения аналоговой величины приводит так же к числовому представлению информации. Передача или хранение сообщений при этом сводятся к передаче или хранению чисел, которые можно выразить в какой-либо системе отсчета. Таким образом, будет получен один из кодов основанный на данной системе счисления, и каждому разряду можно поставить в соответствие какой-либо электрический параметр, например, амплитуду сигнала.

P=12 35=2B₁₂

P=4 35=203₄

P=2 35=100011₂

Очевидно, что чем больше основание систем счисления, тем меньшее число разрядов требуется для его представления. Но в этом случае существенно повышаются требования к аппаратуре формирования и распознавания сигналов. С точки зрения компромисса между этими показателями оптимальной будет система счисления с основанием 3, и незначительно ей уступают 2-чная и 4-чная. Предпочтение отдается двоичной в силу простоты её физической реализации.

Докажем:

С ростом основания СС и логические элементы вычислительных устройств должны иметь большее число устойчивых состояний. С учетом этого в качестве показателя эффективности может быть выбрано число, равное произведению количества различных символов «q» на количество разрядов N. Введем коэффициент эффективности c=q*N, который называют показателем экономичности системы. Наиболее эффективной будет система, обеспечивающая минимум значения «c». Примем, что каждый разряд числа представлен не одним элементом с «q» устойчивыми состояниями, а «q» элементами, каждый из которых имеет одно устойчивое состояние. Тогда показатель «c» определит условное количество оборудования, которое нужно иметь для представления чисел в данной системе. Максимальное число, которое можно записать в q-чной системе счисления: A_max=q^N-1. Следовательно:

Для любой системы:

Будем считать «q» непрерывной величиной (а не дискретной). Значение «с» рассмотрим как функцию от «q». Если за единицу измерения оборудования принять один элемент с одним устойчивым состоянием, до для сравнения двух систем счисления можно ввести относительный показатель F, позволяющий сравнить любую систему счисления с двоичной.

Проанализировав функцию на экстремум, получим минимум этой функции. q=2,72

С точки зрения затрат на оборудования наиболее экономичной является СС с основанием 3.