Загальний опис алгоритму
1. Вибір загального виду моделі, котрим буде описуватись задана залежність.
2. Вибір зовнішніх критеріїв оптимальності та свободи вибору.
3. Вибір загального виду опорної функції(для багаторядних алгоритмів МГУА).
4.
Надамо нульові значення лічильнику
числа моделей
і лічильнику числа рядів
.
5.
Згенеруємо нову часткову модель.
Визначимо значення основних критеріїв
на ній. Визначимо
.
6.
Якщо
,
то k=0, r=r+1. Запишемо загальний критерій
моделей
.
Якщо r=1, то йдемо на крок 5, інакше – на
крок 7.
7.
Якщо
,
то йдемо на крок 8, інакше відберемо
найкращих моделей згідно з зовнішнім
критерієм і йдемо на крок 5.
8. Із найкращих моделей по критерію регулярізації оберемо кращу модель.
Відновимо аналітичний вид найкращої моделі, використовуючи гьоделівську нумерацію.
Гібридний алгоритм навчання мережі rbf
В гібридному алгоритмі процес навчання мережі розбивається на два етапи:
1) підбір лінійних параметрів мережі (ваги вихідного шару) при застосуванні методу псевдоінверсії;
2)
адаптація нелінійних параметрів
радіальних функцій (центру
та
ширини
цих
функцій).
Обидва
етапи тісно переплітаються. При фіксації
конкретних значень центрів та ширини
радіальних функцій (на першій ітерації
це будуть початкові значення) за один
крок, з застосуванням декомпозиції SVD,
підбираються величини лінійних ваг
вихідного шару. Така фіксація параметрів
радіальних функцій дозволяє визначити
значення самих функцій
для
і
,
де
- це номер радіальної функції, а
–
номер чергової навчальної пари
.
Чергові
збудження
генерують в прихованому шарі сигнали,
що описуються векторами
,
де 1 позначає одиничний сигнал поляризації.
За ними слідує вихідний сигнал мережі
-
,
причому
вектор
містить
ваги вихідного шару,
.
При
наявності
навчальних
пар отримуємо систему рівнянь
,
яку у векторному вигляді можна записати так:
.
При
застосуванні гібридного методу на етапі
підбору вихідних ваг, вектор
замінюється
вектором очікуваних значень
,
та
утворена при цьому система рівнянь
вирішується
за один крок з використанням псевдо
інверсії.
.
В алгоритмі розрахунку псевдоінверсії застосовується декомпозиція SVD.
На другому етапі, при фіксованих значеннях ваг, збуджуючі сигнали пропускаються по мережі до вихідного шару, що дозволяє розрахувати величину помилки для послідовності векторів .
Далі
відбувається повернення до прихованого
шару (зворотне поширення). По величині
помилки визначається вектор градієнта
цільової функції відносно конкретних
центру
та ширини
.
Для подальшого викладення припустимо,
що використовується модель мережі типу
HRBF з діагональною формою масштабуючої
матриці Q.
Це значить, що кожна радіальна функція
у загальному вигляді визначається як:
,
де
сумарний сигнал нейрона
описується
виразом:
.
При наявності навчальних пар, цільову функцію можна задати у вигляді:
.
В результаті диференціювання цієї функції отримуємо:
,
.
Застосування градієнтного методу найскорішого спуску дозволяє провести уточнення центрів та ширини радіальних функцій у відповідності до формул:
,
.
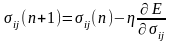Уточнення нелінійних параметрів радіальної функції завершує черговий цикл навчання. Багатократне повторення обох етапів призводить до повного та швидкого навчання мережі, особливо коли початкові значення параметрів радіальних функцій близькі до оптимальних.
На практиці виділені етапи в різній степені впливають на адаптацію параметрів. Як правило, швидше функціонує алгоритм SVD (за один крок знаходить локальний мінімум функції). Для вирівнювання цієї диспропорції, одне уточнення лінійних параметрів зазвичай супроводжується декількома циклами адаптації нелінійних параметрів.