Навчаня нм за допомогою процедури зворотнього поширення

Повний алгоритм навчаня НМ за допомогою процедури зворотнього поширення включає наступні кроки .

Нехай на входи НМ поданий один з можливих образів.

1. Покладемо .

2. Розраховуємо послідовно значення виходів для n-го шару (n=1,2,…,N)...

3. Розраховуємо величини для нейронів вихідного шару:

Визначаємо .

4. Використовуючи рекурентну формулу , розраховуємо через і для всіх попередніх шарів

n=N-1,N-2,…,1 за формулою: .

5. Коректуємо ваги в НМ відповідно до процедури

На цьому перша ітерація (t) закінчується.

6. Розраховуємо .

Якщо , то СТОП.

Інакше йдемо на крок 1 (t+1) ітерації.

Даний алгоритм розрахунку величин ілюструється на Рис. 1, 2, 3, 4.

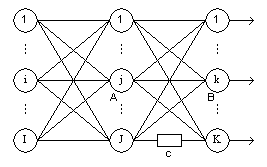
y_i^(n-1)

y_j⁽ⁿ⁾

w_{i j}⁽ⁿ⁾

w_{j k}⁽ⁿ⁺¹⁾

Рис. 1.

Рис. 2.

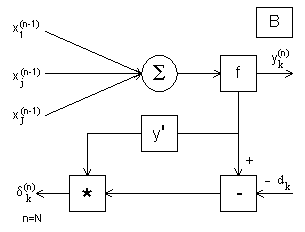
Рис. 3.

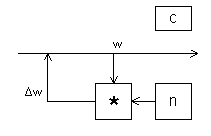
Рис. 4.

Метод спряжених градієнтів для навчання нейронної мережі Back Propagation

Метод спряжених градієнтів (СГ) дає поліпшення швидкості збіжності в порівнянні з методом найшвидшого спуску. Однак, як і метод найшвидшого спуску, він є методом локальної оптимізації.

У нейронних мережах цільова функція (ц.ф.), яку необхідно мінімізувати – це середня помилка на всій множині навчальних зразків. Вона дорівнює

(4.1)

де - множина навчальних зразків.

Для тришарової мережі з N вхідними вузлами, включаючи граничний вузол, J схованими вузлами і M вихідними вузлами вектор ваг W містить NJ+MJ компонент. У формулі (4.1) M - число вихідних вузлів, - бажаний вихід для навчального зразка t, а - реакція (вихідний сигнал мережі) на зразок t.

Алгоритм СГ, як і більш загальний алгоритм спряжених напрямків, набув застосування в області оптимізації завдяки широкому класу проблем, для яких він забезпечує збіжність до оптимального рішення за кінцеве число кроків. Це суттєве поліпшення в порівнянні з методом найшвидшого спуску, що вимагає нескінченного числа ітерацій для пошуку мінімуму функції .

Алгоритм навчання нейронної мережі

Крок0. Покласти . Ініціалізувати ваговий вектор і обчислити градієнт . Покласти вектор початкового напрямку .

Крок1. Знайти скаляр , що мінімізує , для чого можна використовувати метод Фібоначчі чи золотого перетину.

Крок2. Якщо , де - припустима точність досягнення мінімуму, то STOP. Інакше - обчислити новий напрямок:

Крок3. Якщо , то новий вектор напрямку

,

інакше покласти

та обчислити новий вектор напрямку

.

Крок 4. Замінити на та на . Перехід на крок 1 наступної ітерації.

Застосування нечіткої нейронної мережі ANFIS в задачі прогнозування.

Розглянемо гібридну систему з механізмом логічного висновку запропонованого Сугено на базі правил ЯКЩО-ТО, яка отримала назву мережі ANFIS (Adaptive Network Based Fuzzy Inference System). Дана система може бути успішно використана для настройки функції належності та настройки бази правил в нечіткій експертній системі. Нижче представлено модель нечіткого висновку Сугено та структурна схема мережі ANFIS.

f₁ = a₁ x + b₁ y + r₁

f ₂= a₂ x + b₂ y + r₂

(а)

(б)

Рис.5.1. (а) схема логічного висновку Сугено (б) еквівалентна структура нейронної мережі ANFIS.

ANFIS мережа використовує наступну базу правил:

я кщо х = А₁ та у = В₁ то f₁ = a₁x + b₁y + r₁

якщо х = А₂ та у = В₂ то f ₂= a₂x + b₂y + r₂ ,

де А_i та В_i є лінгвістичними змінними.

Шари даної нечіткої нейронної мережі виконують такі функції:

Шар 1. Кожен нейрон даного шару є нейроном, що перетворює вхідний сигнал х чи у за допомогою функції належності (фазифікатор). Найчастіше використовують дзвіноподібну функцію

(5.1)

чи функцію Гауса

(5.2)

Шар 2. Кожен нейрон в цьому шарі позначений як  здійснює множення вхідних сигналів, моделюючи логічну операцію AND і посилає на вихід

(5.3)

По суті, кожен нейрон представляє активуючу силу правила. (Фактично будь-який оператор Т-норми, що узагальнює операцію AND може бути використаний в даних нейронах).

Шар 3. Кожен нейрон в даному шарі обчислює нормовану силу правила:

(5.4)

Шар 4. На даному шарі в нейронах формуються значення вихідних змінних:

(5.5)

Шар 5. В останньому шарі отримується вихідний сигнал нейронної мережі та виконується дефазифікація результатів:

(5.6)

Нейронна мережа архітектури ANFIS в даній роботі навчається за допомогою градієнтного методу.

Нехай Х1 може приймати r лiнгвiстичних значень.

Х2 – k лiнгвiстичних значень.

Створюється повна база правил - на всi можливi комбiнацii складається таблиця.

де y*- бажаний вихiд.

Метод навчання НМ ANFIS

Нехай - описується - центр iнтервалу, характеристика ширини iнтервалу.