Запасы устойчивости системы по фазе и по амплитуде
Определяем практическим путем.
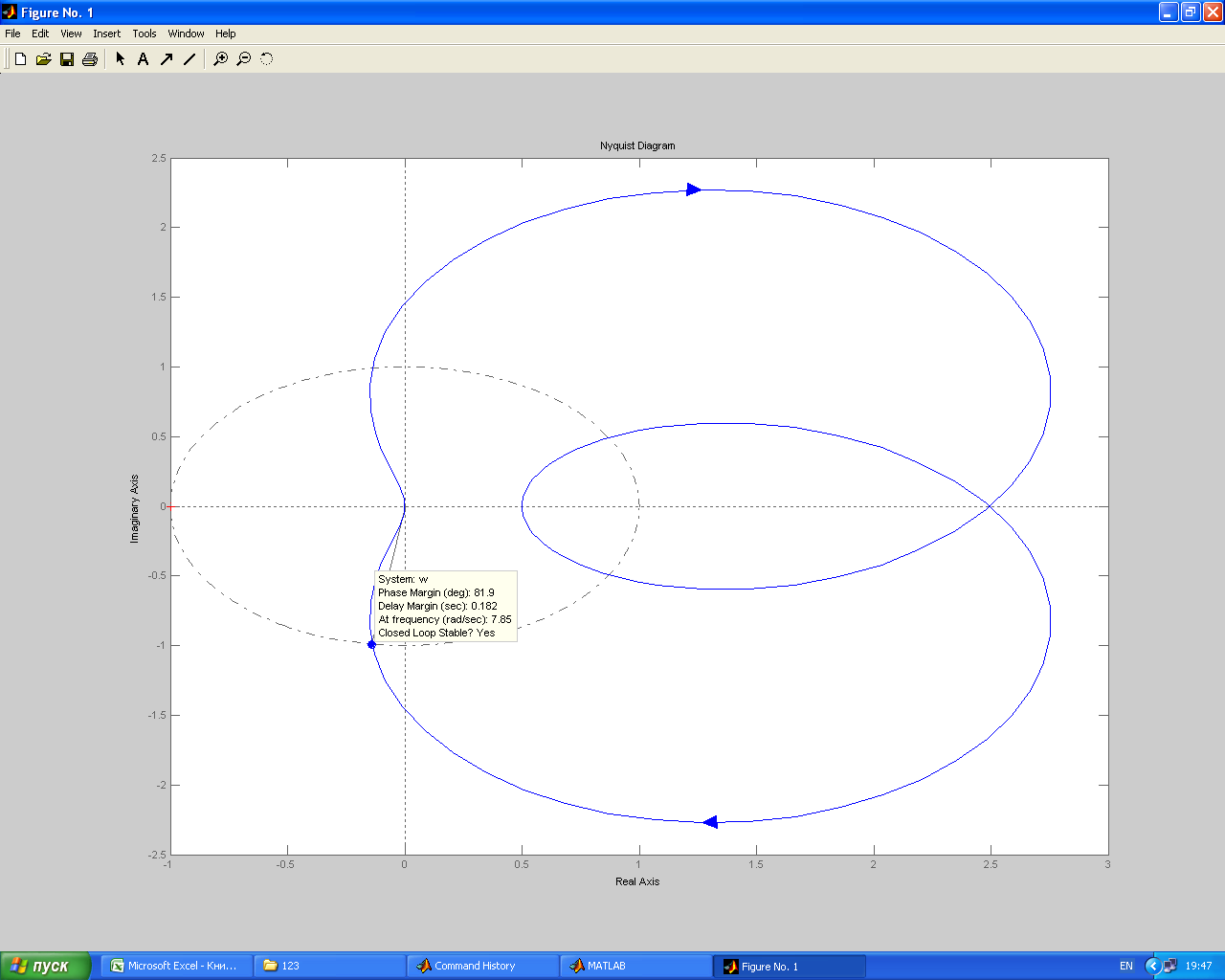
Запас устойчивости системы по амплитуде:
.
Запас устойчивости системы по фазе:
.
Передаточная функция замкнутой системы и проверка вывода пункта №8 с помощью частотного критерия Михайлова
>> w1=tf([0.56,7.475,20.25,15],[0.15,1.3,6.9,25,30]);
>> w2=feedback(w1,1)
Transfer function:
0.5625 s^3 + 7.5 s^2 + 20.25 s + 15
---------------------------------------------
0.15 s^4 + 1.85 s^3 + 14.4 s^2 + 45.25 s + 45
Структурная схема замкнутой системы
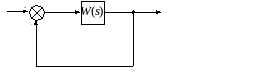
Проверим устойчивость замкнутой системы с помощью частотного критерия Михайлова.
Формулировка критерия Михайлова.
Замкнутая САУ будет устойчивой, если годограф Михайлова, начинаясь на положительной действительной полуоси, с ростом частоты огибает против часовой стрелки начало координат, проходя при этом последовательно n квадрантов комплексной плоскости (где n - порядок характеристического уравнения).
Характеристическое уравнение:
D(p)=
Исходным выражением для определения устойчивости по критерию Михайлова является частотный характерестический полином системы, который определяется из характерестического уравнения заменой оператора p на оператор iw
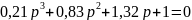
D(iw)=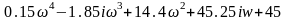
Мы получили функцию комплексного переменного, которую можно представить в виде суммы действительной и мнимой части.
В нашем случае
V(iw)
= 
;
.
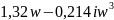
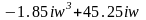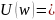
=0
=0
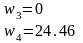
V(8.1)=616.645
V(-8.1)=-616.645
V(5.5)=59i
V(-5.5)=-59i
U(0)=-0.1667*0+1.5=1.5
U(0)=
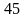
U(24.46)=
Годограф
W |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
10 |
15 |
U |
45 |
30.75 |
-10.2 |
-72.45 |
-147 |
-221.25 |
-279 |
105 |
4398.75 |
V |
0 |
43.4i |
75.7i |
85.8i |
62.6i |
-5i |
-128.1i |
-1397.5i |
-5565i |
Михайлова (в схематичном виде):
Критерий Михайлова:
Замкнутая САУ будет устойчивой, если годограф Михайлова, начинаясь на положительной действительной полуоси, с ростом частоты огибает против часовой стрелки начало координат, проходя при этом последовательно n
квадрантов комплексной плоскости (где n – порядок характеристического уравнения).
В данном случае годограф соответствует критерию Михайлова, значит, замкнутая САУ устойчива.
Построение переходной функции замкнутой системы и основные показатели качества регулирования (перерегулирование и время регулирования) в системе.
w=tf([0.56,7.475,20.25,15],[0.15,1.3,6.9,25,30])
Transfer function:
0.5625 s^3 + 7.5 s^2 + 20.25 s + 15
---------------------------------------------------
0.15 s^4 + 1.288 s^3 + 6.9 s^2 + 25 s + 30
>> w=feedback(w,1)
Transfer function:
0.5625 s^3 + 7.5 s^2 + 20.25 s + 15
---------------------------------------------
0.15 s^4 + 1.85 s^3 + 14.4 s^2 + 45.25 s + 45
>> step(w)
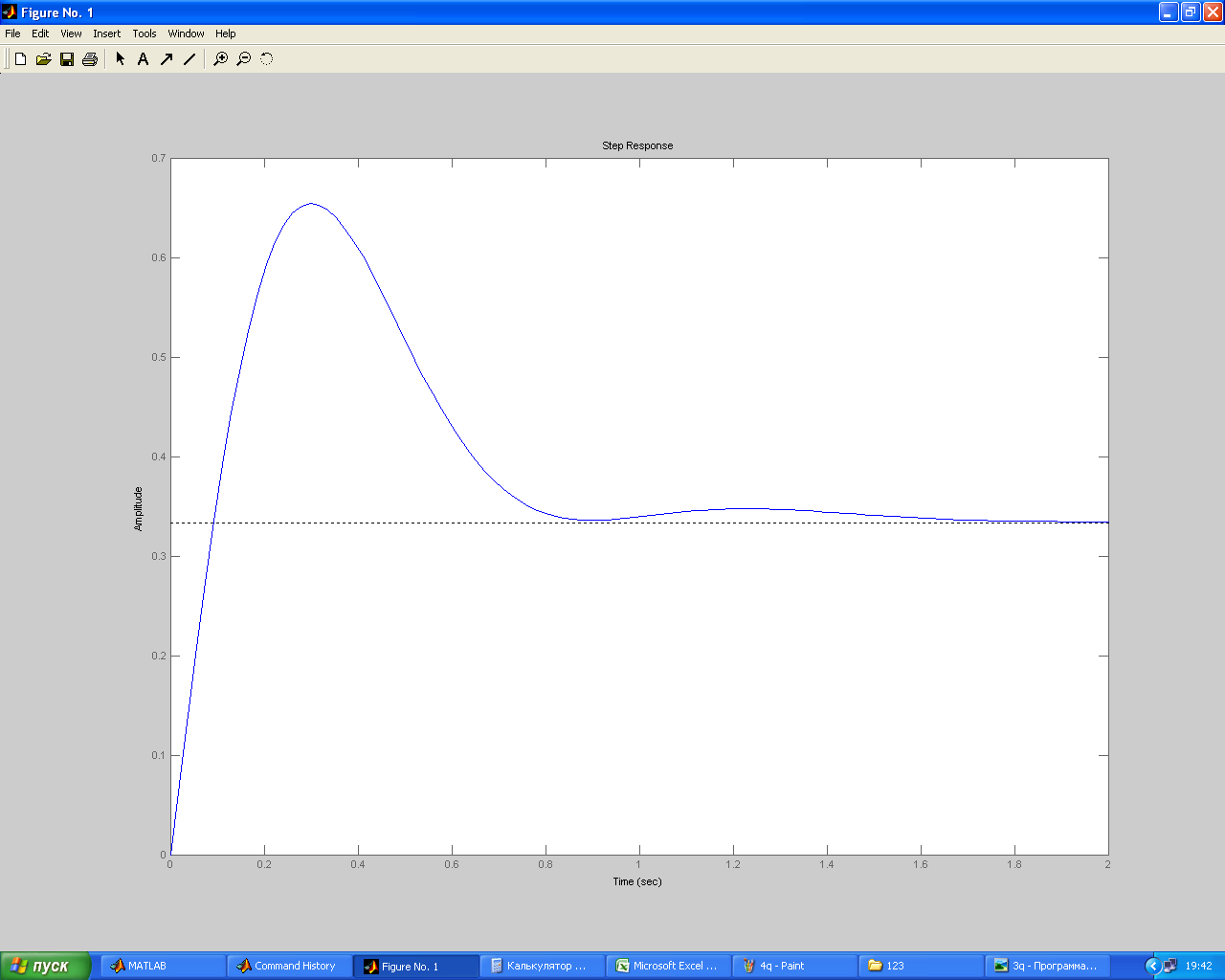
Основные показатели качества переходного процесса:
1) время регулирования:
Tр = 3.9 cек;
2) перерегулирование:
;
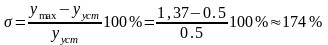Корневые критерии позволяют оценить качество переходного процесса по виду корней характеристического уравнения.
Для оценки быстродействия системы, используют понятие степень устойчивости. Под степенью устойчивости η понимают абсолютное значение вещественной части ближайшего к мнимой оси корня.
Степень колебательности (m) – равна минимальному (для всех корней характеристического уравнения) отношению действительной и мнимой частей корня.
С помощью команды pzmap получим корневой портрет замкнутой системы и определим корневые оценки переходного процесса: