9. Побудова графіків залежностей

   1. ^{Побудова графіка струму і(t).}

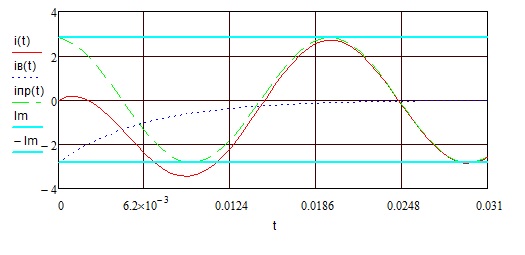
2. Побудова графіка спаду напруги на активному опорі u_R(t)

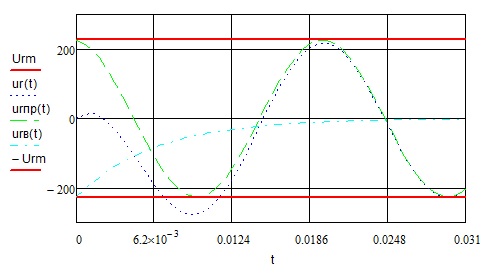
3. Побудова графіка спаду напруги на індуктивному опорі u_L(t)

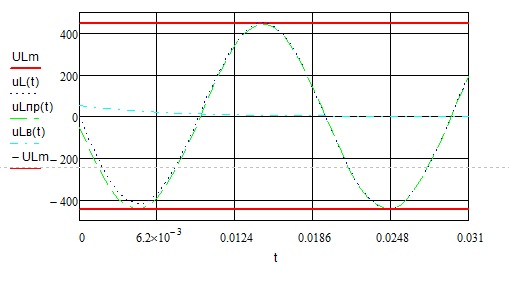
Завдання 2

В активно-ємнісне коло (рис 2), яке вмикається на синусоїдальну напругу u(t)=Umsin(ωt+ψ), має задані величини E,R,С. В колі відбувається комутація шляхом замикання вимикача S. Потрібно визначити залежність перехідного струму і спадів напруг на елементах кола від часу та побудувати графіки залежності i(t),u_R(t),u_С(t).

Порядок розрахунку

Аналіз перехідного процесу в RС-колі проведемо із наступних розрахункових операцій.

1. Побудова розрахункової схеми заміщення rс-кола і аналіз вихідних даних

Схема заміщення RС-кола має наступний вигляд:

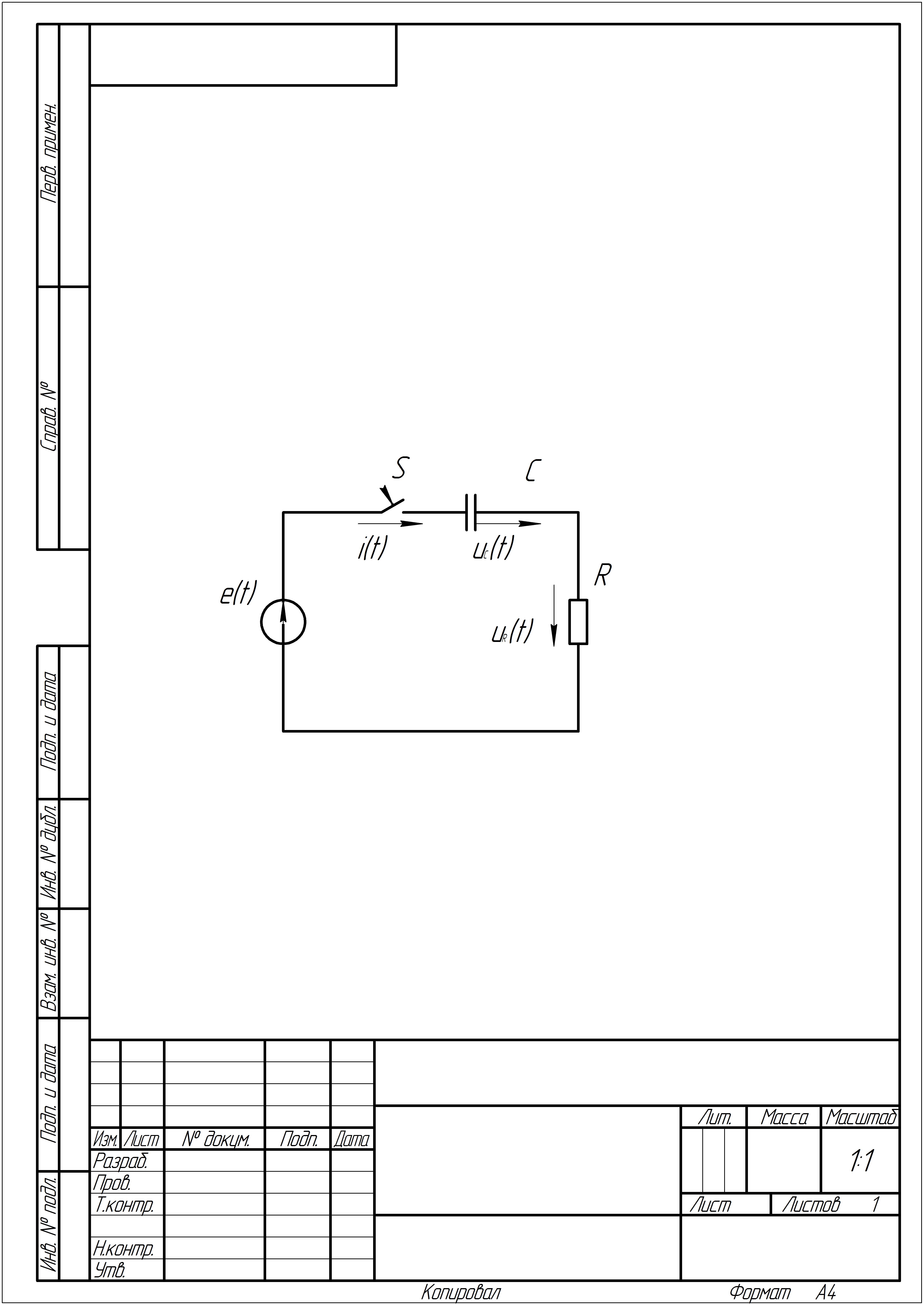
Рис 2 Розрахункова схема заміщення RС-кола

Вихідні дані: Em=500В, С=290мкФ=290∙10^-6Ф, R=80Ом, ψ_e=160°,f=50Гц

Визначимо, аналогічно як в RL-колі, миттєві та комплексні значення ЕРС, спадів напруги, струму, повного опору та період і частоту змінного струму згід­но вихідних даних, і виконуємо наступні розрахункові операції:

1. Визначення миттєвого значення ЕРС:

Де ω=2

Визначення комплексного значення ЕРС в показниковій та алгебраїчній формах:

а) в показниковій формі :

Підставимо значення отримаємо:

Тоді:

б) в алгебраїчній формі:

Проводимо перетворення з показникової форми до алгебраїчної за допомогою формули Ейлера, тобто:

1.2 Визначення комплексних значень, модулів та аргументів повних опорів:

а) в алгебраїчній формі:

б)в показниковій формі :

1.3 Визначення комплексних значень струмів і спадів напруг в показниковій та алгебраїчній формах:

а) в показниковій формі:

б)алгебраїчній формі:

1.4 Запишемо миттєві значення ЕРС, струмів і спадів напруг на активному та індуктивному опорах:

2. Аналіз початкових умов

3. Складання диференціального рівняння і визначення постійної часу.

1. За другим законом Кірхгофа для RL-кола змінного струму (рис 2), маємо:

2. Продиференціюємо дане рівняння:

(1)

Маємо лінійне неоднорідне диференціальне рівняння першого порядку з сталими коефіцієнтами.

3. Приведемо диференціальне рівняння до виду, який містить постійну інтегрування. Для цього у рівняння (1) замінимо добуток RС на Т_С тоді маємо:

(2)

Де: T_С—постійна часу кола

3. . Складаємо характеристичне рівняння і визначаємо його корені

   1. щоб скласти характеристичне рівняння потрібно взяти першу похідну від рівняння (2), маємо:

Т_С∙р+1=0.

2. Визначаємо корінь характеристичнного рівняння:

Так як. то підставивши значення вихідних даних будемо мати

Тоді,

3. . Розв'язання диференціального рівняння:

Перехідний процес, який проходить в колі, можна розглядати як такий що складається з накладених один на одного процесів — примушеного, який настав відразу, і вільного, який має місце тільки протягом перехідного режиму.

Тому, можна записати, що перехідна напруга конденсатора дорівнює сумі примушеної та вільної напруг:

(3)

Примушена напруга дорівнює:

Вільний струм дорівнює:

(4)

Тоді рівняння (3), можна записати:

(5)

Де: А- постійна інтегрування