Завдання 2

1) Визначнити матрицю

1.1) Зворотня матриця

2) Ранг матриці

3) Власні значення

3.1) Власні вектора

4) Ідемпотентность матриці

Матриця Ідемпотента так як рівна Р

5)Інвалютивність матриці

Матриця I інвалютівна, так як при округленні =

Висновок : З допомогою Matchad записав функцію і визначив область визначення і межі області визначення. Далі визначив що функція парна і неперіодична. Знайшов точки перетину, розриву і асимптоти. Визначив проміжки монотонності і точки екстремумів і побудував графік.

В 2 завданні визначив і знайшов зворотню матрицю, а також ранг матриці. Знайшов власні значення і вектора. Дослідив матрицю на Ідемпотентность, і визначив що вона Ідемпотента, а також інвалютівна.

Друга частина

На тему: «Розв’язок СЛАР та побудування тривимірних графиків у Matlab»

Мета роботи

Метою другої частини є набуття навичок практичних досліджень методів розв’язання систем лінійних алгебраїчних рівнянь (СЛАР) в середовищі Матлаб, закріплення та поглиблення знань з питань вищої математики, фізики. Отримання навиків побудови тривимірних графиків, форматування та редагування графічних вікон.

Зміст другої частини курсової роботи

Друга частина курсової роботи присвячена аналізу систем лінійних алгебраїчних рівнянь середовищі Матлаб та побудові тривимірних графиків та складається з двох завдань.

Варіант 15

Умови другої частини курсової роботи

Перше завдання

Потрібно:

1. Дослідити систему на наявність розв’язків.

2. Розробити блок-схему алгоритму пошуку розв’язку (згідно табл. 4).

3. Розв’язати СЛАР за допомогою

   • методу Зейделя;

Друге завдання

№ варіанту	Функція	Межі зміни аргументів (x, у)
15	z=y/(x*x+y*y+3*x*y)	-2 : 0.1 : 2

Потрібно:

Побудувати поверхні функцій (табл. 5). Графіки повинні мати назву і найменування осей. Всі характерні ділянки (опуклості, угнутості, екстремуми і т.п.) повинні бути вказані і прокоментовані безпосередньо на графіку.

Теоретичні відомості

Теоретичний матеріал для першого завдання

Системою лінійних алгебраїчних рівнянь (СЛАР) називають систему виду:

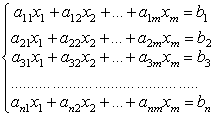
де х_і, (і=1,…,n) – невідомі; b_i, (і=1,…,n) – вільні члени системи; a_ij, (і, j = 1,…,n) – коефіцієнти системи.

В матричному вигляді рівняння системи прийме вигляд:

А×Х=В,

де Х={x₁, x₂,…, x_n} – вектор невідомих; B={b₁, b₂,…, b_n} – вектор вільних членів;

A={a₁₁, a₂₁,…, a_mn} – матриця коефіцієнтів СЛАР.

Розв’язком системи лінійних алгебраїчних рівнянь називають вектор X, координати якого {x₁, x₂,…, x_n} при підстановці у систему, що розв’язують, перетворюють кожне рівняння системи в тотожність .

Кількість невідомих m в системі називають порядком СЛАР. Систему лінійних алгебраїчних рівнянь називають сумісною, якщо вона має хоча б один ненульовий розв’язок. В протилежному випадку СЛАР називають несумісною. СЛАР називається визначеною, якщо вона має тільки один розв’язок (випадок, коли m=n). Систему називають невизначеною, якщо вона має безліч розв’язків (mn). Система називається виродженою, якщо головний визначник системи дорівнює нулю. Система називається невиродженою, якщо головний визначник системи не дорівнює нулю.

Дві системи називаються еквівалентними, якщо ці системи сумісні, визначені і мають однаковий розв’язок.

СЛАР можна розв'язати на ЕОМ чисельними методами, якщо вона сумісна, визначена, невироджена.

Для розв’язання СЛАР на ЕОМ традиційно використовують дві групи чисельних методів:

• точні (метод Гауса, метод Крамера);

• наближені (метод послідовних ітерацій, метод Зейделя).

До точних методів відносять методи, які дозволяють отримати точний розв’язок системи за відповідну кількість операцій перетворення без урахування похибок заокруглення.

Метод Гауса-Зейделя можна розглядати як модифікацію методу Якобі. Основна ідея модифікації полягає в тому, що нові значення використовуються тут одразу ж у міру отримання, в той час як у методі Якобі вони не використовуються до наступної ітерації:

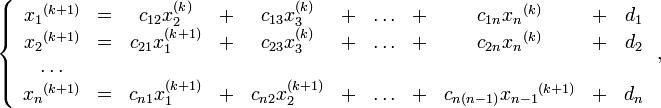
де

Таким чином i-тий компонент (k+1)-го наближення обчислюється за формулою:

При виконанны другого завдання другої частини курсової роботи необхідно пам’ятати:

В системі MATLAB передбачено кілька команд і функцій для побудови тривимірних графіків. Значення елементів числового масиву розглядаються як z-координати точок над площиною, яка визначається координатами x і y. Можливо кілька способів з'єднання цих точок. Перший з них - це з'єднання точок у перерізі (функція plot3), другий - побудова сітчастих поверхонь (функції mesh і surf). Поверхня, побудована за допомогою функції mesh, - це сітчаста поверхня, осередки якої мають колір фону, а їх межі можуть мати колір, який визначається властивістю EdgeColor графічного об'єкта surface. Поверхня, побудована за допомогою функції surf, - це сітчаста поверхня, у якої може бути заданий колір не лише межі, а й осередків; останнє управляється властивістю FaceColor графічного об'єкта surface.