Перша частина

На тему: «набуття навичок практичних досліджень функцій та матриць, закріплення та поглиблення знань з питань вищої математики, фізики»

Мета роботи

Основною метою першої частини курсової роботи є набуття навичок практичних досліджень функцій та матриць, закріплення та поглиблення знань з питань вищої математики, фізики.

Зміст першої частини курсової роботи

Перша частина курсової роботи присвячена аналізу нелінійних функцій та матриць в середовищі АСОД Маткад та складається з двох завдань.

Робота виконується студентом за індивідуальним завданням, яке містить необхідні вихідні дані.

Варіант 15

Перше завдання

Потрібно:

1. Знайти область визначення функції й з'ясувати характер поведінки функції (обчислити границі) на межах області визначення, а також, коли , якщо функція там визначена;

2. З'ясувати, чи є функція парної, непарною, загального виду;

3. З'ясувати, чи є функція періодичною;

4. Знайти точки перетинання функції з осями координат;

5. Знайти точки розриву функції й з'ясувати характер розривів;

6. Знайти асимптоти функції;

7. Обчислити . Використовуючи похідну, визначити проміжки монотонності функції й точки екстремумів;

8. Обчислити . Використовуючи похідну другого порядку, визначити проміжки опуклості уверх (униз) функції й точки перегину.

9. Побудувати графік функції.

Друге завдання

Потрібно:

1. Знайти визначник матриці та обернену матрицю, якщо така існує;

2. Визначити ранг матриці;

3. Знайти власні значення та власні вектори матриці;

4. Довести, що матриця Р є ідемпотентною;

5. Показати, що матриця I = 2P - E інволютивна.

Теоретичні відомості

Для виконання першого завдання першої частини ккурсової роботи необхідно повторити наступний теоретичний матеріал.

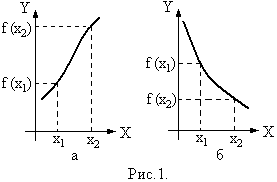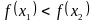В изначення. Будемо казати, що функція монотонно зростає (спадає) на , якщо для таких, що , буде витікати (рис.1(а)) ( (рис.1(б))).

Нехай функція неперервна на і диференційована на , до того ж ( 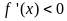) на , тоді зростає (спадає) на цьому сегменті.

Таким чином, для того, щоб дослідити функцію на зростання і спадання, визначити проміжки монотонності треба:

1. Знайти область визначення функції (нехай для конкретики це буде ).

2. Обчислити похідну .

3. Знайти такі аргументи ,..., функції з її області визначення, в яких

а) похідна не існує;

б) .

Ц і точки розіб’ють всю область визначення на частки, де зберігає знак, а зберігає характер монотонності. Для зручності й наочності всі ці точки разом з областю визначення має сенс винести на координатну вісь ОХ (рис.2).

4. На кожному з отриманих на попередньому кроці відрізків області визначення встановити знак і відповідний характер монотонності : якщо для 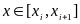, то на сегменті функція зростає (спадає).

Визначення. Нехай функція визначена на . Кажуть, що має локальний максимум (локальний мінімум) в точці , якщо існує такий окіл точки , що

.

Локальний максимум (мінімум) називається строгим, якщо окіл можна обрати так, що

.

Точки локального мінімуму і локального максимуму функції називаються точками її локального екстремуму.

Необхідна умова локального екстремуму. Нехай функція визначена на і має локальний екстремум в точці . Тоді обов’язково виконується одна з наступних умов:

1. в точці не існує похідна функції ;

2. .

Таким чином, точки, в яких функція недиференційована, чи її похідна дорівнює 0, є точками, підозрілими на екстремум: в цих точках екстремум може бути, а може не бути. Треба застосовувати для таких підозрілих точок достатні умови екстремуму.

Перша достатня умова локального екстремуму. Нехай функція визначена на і диференційована на цьому інтервалі скрізь, за винятком, можливо, точки , в якій функція неперервна. Якщо існують такі лівий і правий напівоколи точки , в кожному з яких зберігає знак, то

1. функція має локальний екстремум в точці , якщо похідна має значення різних знаків в відповідних напівоколах, а саме: якщо при проходженні через точку змінює знак з «+» на «-», то — точка локального максімума, якщо знак похідної змінюється з «-» на «+» — локального мінімуму;

2. функція не має локального екстремуму в точці , якщо похідна справа і зліва від має значення однакових знаків.

Друга достатня умова локального екстремуму. Нехай функція визначена на і виконуються умови:

1. ;

2. в точці існує похідна другого порядку ,

тоді має локальний екстремум в точці , а саме: локальний максимум, якщо

,

локальний мінімум, якщо

.

Третя достатня умова локального екстремуму. Нехай найменший порядок похідної функції в точці , яка не дорівнює 0, це , тобто

.

Тоді

1. якщо — парне, то має локальний максимум в точці , якщо

,

чи локальний мінімум, якщо

;

2. якщо — непарне, то екстремуму в точці немає.