Виды дисперсии
Существует целая группа причин возникновения дисперсии (рис. 11). Как видно из рисунка, дисперсия может возникать при большом количестве распространяемых по волокну мод (модовая дисперсия), которая зависит от типа профиля показателя преломления в используемом волокне. Дисперсия возникает из-за некогерентности источников излучения и наличия определенного спектра (а не одной длины волны) в передаваемом сигнале (хроматическая дисперсия). В реальных градиентных и одномодовых волокнах существенной может оказаться "профильная" дисперсия, которая возникает из-за флуктуации профиля показателя преломления (ППП), вызванной различными причинами.
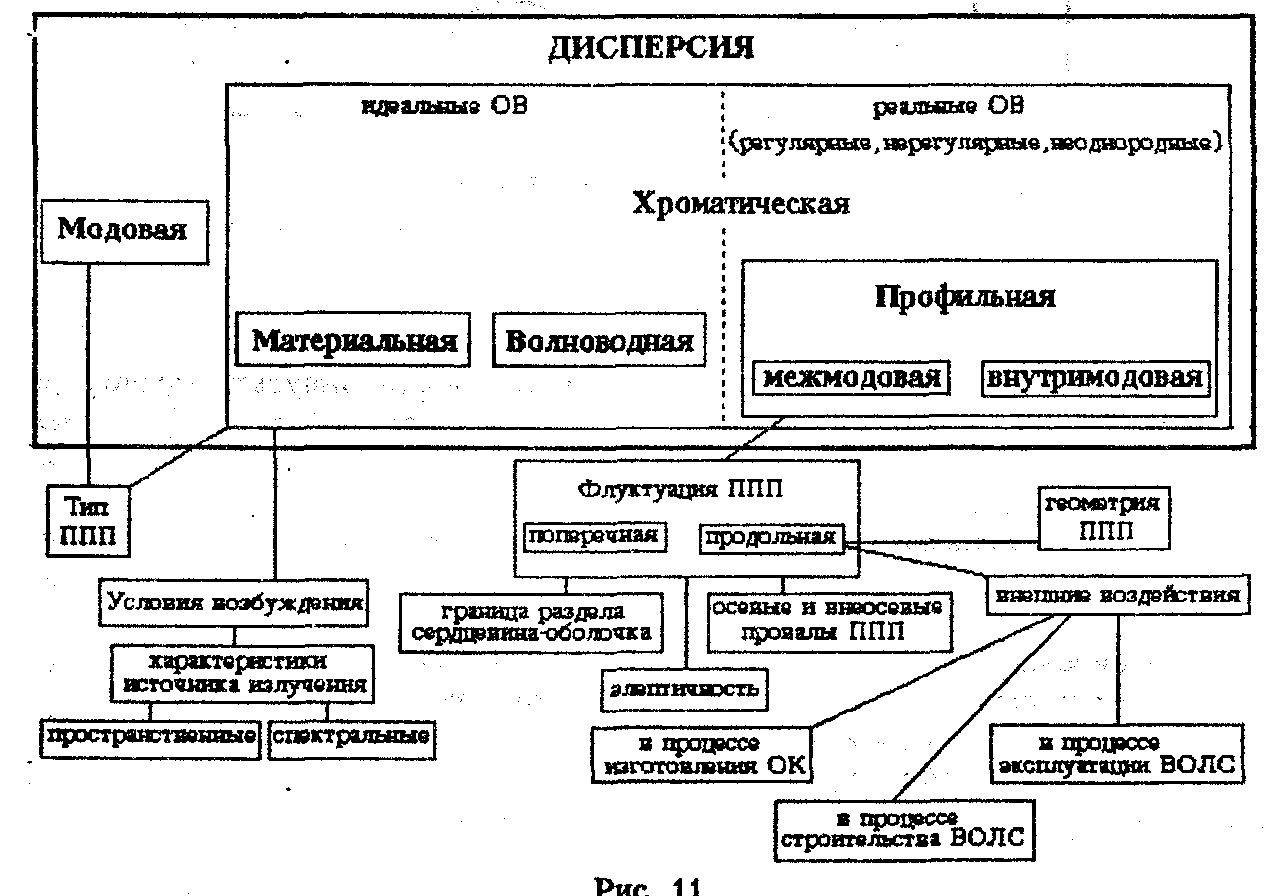
Модовая дисперсия
В оптических кабелях, выполненных на многомодовых волокнах, наибольший вклад в уширение импульсов вносит модовая дисперсия. Процесс распространения электромагнитной волны в оптическом волокне можно анализировать методами геометрической оптики и методами волновой теории путем решения уравнений Максвелла. Первый метод более прост и пригоден при инженерном подходе в решении конкретных задач, второй метод целесообразен для детального исследования характеристик световодов.
Разные моды имеют различную скорость распространения. В геометрической интерпретации соответствующие модам лучи идут под разными углами, проходят различный путь в сердцевине волокна и, следовательно, поступают на выход с различной задержкой.
Следует раздельно рассмотреть процесс возникновения модовой дисперсии в ступенчатых и градиентных волокнах. В кабелях со ступенчатыми волокнами скорость всех лучей, зависящая от коэффициента преломления сердцевины, одинакова и составляет v = c/n1 . Величина модовой дисперсии в таких волокнах определяется из выражения (11) и (12). Величину параметра Δ (относительное соотношение показателей преломления) можно определить по формуле (3), либо по упрощенной формуле:
Δ ≈ (n1-n2)/n1. (38)
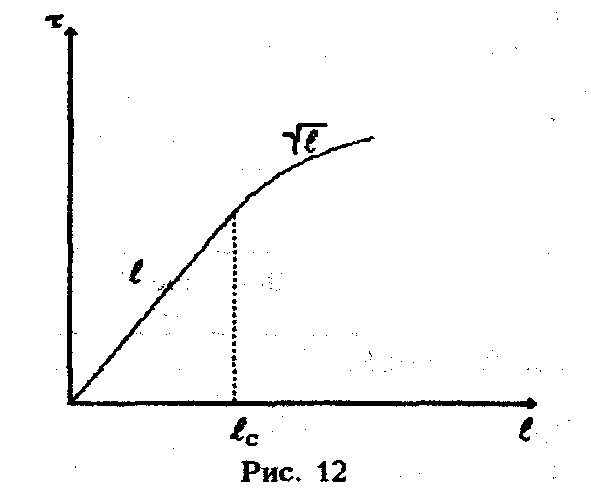
Длина связи мод (5 - 7 км для ступенчатого волокна) - это длина оптического волокна, после прохождения которой в результате взаимного преобразования мод на нерегулярностях (обмен энергии между модами и их высвечивание) соотношение между мощностями различных мод становится практически постоянным. Модовая дисперсия в этом случае возрастает уже не по линейному, а по корень-квадратичному закону.
На рис. 12 представлена типовая зависимость τмод(ℓ)-
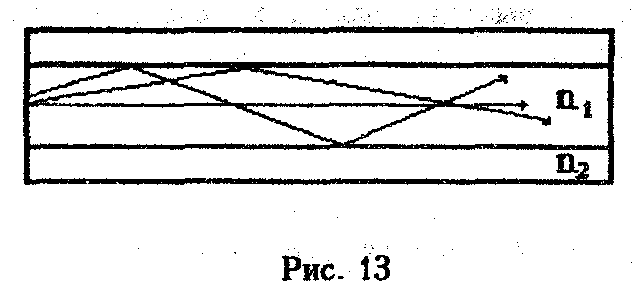
Лучевая модель, иллюстрирующая механизмы возникновения модовой, дисперсии в ступенчатых волокнах, показана на рис. 13.
В градиентных волокнах различные лучи также проходят различный путь. Однако их скорость v=c/n различна. Околоосевые лучи распространяются по короткой траектории, однако в среде со сравнительно высоким n, т.е. с малой скоростью, а периферийные лучи - по длинной траектории, но в основном в среде с низким n, т.е. с большой скоростью (рис. 14).
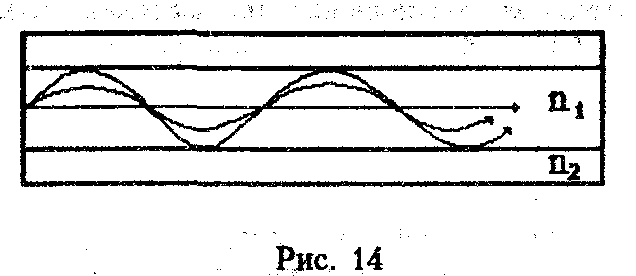
В целом задержка мод оказывается приблизительно одинаковой, а уширение импульсов по сравнению со ступенчатыми волокнами снижается более чем в 10 раз.
Величина модовой дисперсии в градиентных волокнах определяется из выражений (13) и (14).
Значение ℓc в градиентных волокнах составляет порядка 10 - 15 км.
В табл. 4 в качестве примера приведены значения модовой дисперсии τмод в ступенчатых и градиентных волокнах при различных длинах линии и различных соотношениях показателей преломления сердцевины и оболочки.
Таблица 4
Длина линии ℓ ,км |
Значение τмод , нс |
|||
ступенчатые ОВ |
градиентные ОВ |
|||
Значение Δ
|
||||
0.01 |
0.006 |
0.01 |
0.006 |
|
10 |
498 |
332 |
2.47 |
1.09 |
20 |
718 |
474 |
3.55 |
1.58 |
30 |
868 |
578 |
4.32 |
1.91 |