5. Численные методы оптимальной фильтрации

Рекуррентные байесовские алгоритмы

Линейный фильтра Калмана

Для линейных моделей динамической системы и измерений:

где

- n-мерный вектор состояния системы,

- m-мерный вектор управления,

- n-мерный вектор случайных возмущений,

, - матрицы размерностью nxn и nxm соответственно, зависящие в общем случае от номера i,

- l-мерный вектор измерений,

- матрица lxn, элементы которой зависят от i,

- l-мерный вектор независимых ошибок измерений, распределенных по нормальному закону,

возможно применение линейной модификации фильтра Калмана, соотношения которого для прогноза и коррекции вектора состояния даны ниже. Соотношения прогноза случайного вектора состояния динамической системы:

,

где

- ковариационная матрица случайных возмущений в канале движения в момент времени i,

- апостериорная ковариационная матрица, характеризующая точность получаемых оценок, может быть получена независим от измерений, заранее.

Соотношения коррекции представлены ниже:

,

- корреляционная матрица ошибок измерений.

Приведенные в данном разделе соотношения подходят для использования только в линейном случае моделей динамической системы и измерений, что встречается редко. Поэтому зачастую требуется решить задачу оптимальной фильтрации для нелинейных систем. Для этого существует квазилинейная модификация фильтра Калмана.

Квазилинейный фильтр Калмана

Квазилинейная модификация фильтра Калмана используется тогда, когда уравнения, описывающие рассматриваемую систему, не поддаются выделению линейного аналитического вида:

,

где

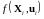- функция состояния,

- вектор-функция измерения.

В таких случаях нет возможности построить точную линейную модель и поэтому рассматриваемую систему линеаризуют.

Уравнения прогноза квазилинейного фильтра для линеаризованной системы:

,

Уравнения коррекции:

6. Комплексирование Бортовых Навигационных Систем и Устройств Ла.

1. Комплексные Системы Измерения Высоты (Ксив).

Назначение КСИВ. Одним из основных навигационных параметров, измеряемых на борту ЛА, является высота. Поэтому измерители высоты входят всех пилотажно-навигационных комплексов ЛА. Задачи навигации, решаемые с помощью КСИВ, весьма многообразны. К числу основных можно отнести следующие:

измерение высоты полета при выполнении взлета и посадки;

контроль высоты при горизонтальном полете на маршруте;

измерение высоты для облета препятствий низколетящими ЛА;

измерение высоты для обеспечения посадки КА на поверхности планет;

и. т. д.

Многообразие перечисленных задач указывает на то, что решение проблемы обеспечения высокой точности и надежности определения высоты ЛА имеет большое значение. Эта проблема может быть решена на основе оптимального комплексирования навигационных систем и устройств, обеспечивающих получение информации о высоте ЛА и работающих на различных физических принципах.

В предыдущих лекциях нашего курса мы рассмотрели навигационные устройства, позволяющие получать данные о высоте полета ЛА. К ним относятся радиовысотомер (РВ), баровысотомер (БВ), вертикальный канал ИНС (инерциальный измеритель высоты -ИИВ). То есть в данном случае выполняется необходимое условие построения КСН - наличие на борту нескольких разнородных навигационных систем или устройств, позволяющих получать информацию об одних и тех же или функционально связанных параметрах.

Ранее мы отмечали, что максимального выигрыша от комплексирования можно ожидать в том случае, когда измерители, входящие в состав КСН, имеют различные спектральные характеристики ошибок. Учитывая это соображение в при построении КСИВ используют следующие комбинации высотомеров:

• радиовысотомер и инерциальный измеритель высоты;

• радиовысотомер и барровысотомер;

• радиовысотомер, баровысотомер и инерциальный измеритель высоты.