Окремі види простих задач

Задачі на знаходження частини від числа та числа за його відомою частиною

Згідно з чинною програмою з математики, розв’язувати прості задачі даних видів учні повинні у 3 класі. Проте в підручнику М. Богдановича для 3 класу немає жодної сюжетної простої задачі - на знаходження частини від числа і лише одна сюжетна задача на знаходження числа за його частиною!

У 2 класі вивчення частин подається лише в порядку ознайом­лення. Підручник 2 класу містить дві прості задачі на знаходжен­ня частини від числа:

№ 845. Довжина мотузки 8 м. Яка довжина половини мотузки?

№ 846. Знайди половину числа 12, третину числа 15 і чверть числа 8.

Не дивно, що учні плутають дії у задачах обох видів. Щоб відрізнити один вид від другого, учні повинні розв’язати багато сюжетних задач, бо лише у сюжетній задачі можна чітко уявити собі 1/3 хлібини, 1/4 від 8 кг цукерок тощо. Велике значення має перший, підготовчий, ступінь роботи над такими задачами.

Задачі на знаходження частини від числа

Перший ступінь - підготовча робота.

1 )

Зафарбуйте ¼ смужки. Що означає частина від цілого? (Тре­ба ціле поділити на 4 рівні частини і взяти одну таку частину.)

Учні практично виконують завдання зі смужкою.

2) Смужка має довжину 18 дм. Відрізали 1/6 смужки. Скільки деци­метрів відрізали? Обчисліть не вимірюючи.

• Що означає 1/6 частина смужки? (Смужку поділили на 6 рів­них частин і відрізали одну таку частину.) Чи можемо, не вимірюючи, обчислити її довжину? (Так. 18 • 6 = 3 (дм).)

• Як знайти 1/6 частину від числа? (Треба число поділити на 6.) А як знайти 1/8 частину від числа? (Треба число поділити на 8.) Що більше - число чи його частина? (Число.) Правильно, бо ціле завжди більше від його частини.

Другий ступінь. Ознайомлення із задачею на знахо, частини від числа.

Петрик назбирав ЗО маслюків, 1/5 усієї кількості мама додала до юшки. Скільки маслюків мама додала до юшки?

• Що тут потрібно знайти? (1/5частину від ЗО маслюків). Як знайти 1/5 від числа? (Потрібно число поділити на 5.) Якою дією розв’яжемо задачу? (Дією ділення.)

Після одержання відповіді для самоперевірки діти повинні порівняти отримане число 6 маслюків з початковим їх числом і переконатися, що частина менша від цілого. Учитель роз’яснює що «ціле» - це не обов’язково один кавун, один гриб, одна хлібина. У цій задачі всі знайдені Петриком гриби - це теж ціле, а 6 грибів це частина від цілого, а саме 1/5 - його частина.

Задачі на знаходження числа за його відомою частиною

Перший ступінь - підготовча робота.

1. У смужці зафарбували 5 дм, що становить 1/3 частину всієї смужки. Яка довжина цілої смужки?

Учитель креслить на дошці смужку завдовжки 5 дм і зафарбовує її.

• Це ціла смужка? (Ні, це лише її частина.) Скажіть: смужка довша чи коротша, ніж заштрихована. (Довша.) Скільки третіх частин містить ціла смужка? (Три третіх.) Учитель видовжує смужку:

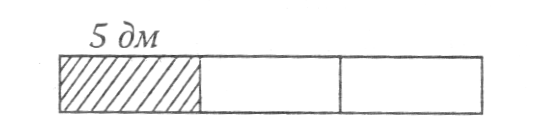
• У скільки разів стала довшою смужка? (У 3 рази.) Як обчислити її довжину? (5 • 3 = 15 (дм).)

2. Оленка з’їла 2 цукерки, що становить 1/4 усіх її цукерок. Скіль­ки всього цукерок було в Оленки?

• Скільки четвертих частин містить ціле? (Чотири.) Якщо така частина - це 2 цукерки, то як знайти ціле? (2 • 4 = 8 ( ц.) . Учитель ілюструє задачу кружечками:

• Якщо відома третина,то як ми знаходили ціле? (Число множили на 3.) Якщо відома 1/5 частина, то як знайти ціле? (Число помножити на 5.) У відповіді одержуємо більше чи менше? (Біль­ше.) Так, бо ціле більше, ніж його частина.

Другий ступінь - ознайомлення із задачею на знаходження числа за його частиною.

Максим подарував товаришеві 7 марок. Це 1/6 усіх марок, які в нього були. Скільки марок було у Максима спочатку?

-7 марок - це ціле чи його частина? (1/6 частина.) А що означає ціле у цій задачі? (Всі марки Максима.) Що ми шукаємо: ціле чи його частину? (Ціле.) Скільки шостих частин містить ціле? (Шість шостих.) Якою дією знайдемо ціле? (Дією множення: 7 * 6 = 42 (м).) Далі діти переконуються, що ціле дійсно біль­ше за його частину: 42 > 7.

На третьому ступені варто подавати задачі обох видів пара­ми; можна подавати взаємообернені задачі.

1. У коробці було 6 олівців, з них 1/3 - прості. Скільки простих олівців було в коробці?

2. У коробці було 2 простих олівці, що становить 1/3 частину від усіх олівців коробки. Скільки олівців у коробці?

Щоразу учні з’ясовують, що вони знаходять: ціле чи його час­тину; більшою чи меншою за дане число має бути відповідь. Якщо більшою, то задачу розв’язуємо множенням, якщо меншою - ді­ленням.

Можна змінювати дані задачі і стежити з учнями за зміною відповіді:

4 квітки - це (1/2,1/6,1/8) усіх квіток на клумбі. Скільки кві­ток на клумбі?

У саду цвіли 24 дерева. Яблунь була 1/2 (1/3,1/4,1/6,1/8) частина від усіх дерев. Скільки яблунь цвіло у саду?

Можна запропонувати учням скласти обернену задачу до да­ної.

Під час диференційованої роботи, поки сильні і середні учні виконують один із названих видів творчої роботи над задачею, слабші повинні пояснити учителеві вибір дії в основній задачі. У разі потреби, для них треба подати ілюстрацію у вигляді ма­люнка, креслення, роздаткового матеріалу.

Задачі на знаходження площі прямокутника

Задачі на знаходження площі прямокутника, згідно з програмою, вивчають у 4 класі, коли вводиться поняття площі.

Ознайомлення з поняттям площі і навчання обчислювати площу прямокутника (як складова змістової лінії «Величини одиниці величин») водночас є підготовчим ступенем для задач цього виду. Учні засвоюють правило: «Щоб обчислити площу прямокутника, треба визначити його довжину і ширину та знайти добуток цих чисел». У підручнику накреслені прямокутники, площу яких потрібно обчислити. Діти вимірюють довжину і ширину кожного прямокутника та обчислюють площу за правилом. Пізніше за відомою площею прямокутника та однією з його сторін учні вчаться обчислювати другу сторону прямокутника.

Робота на другому ступені мала б включати прості сюжетні задачі на знаходження площі та однієї зі сторін прямокутника. На жаль, сюжетних задач у підручнику М. Богдановича немає, є лише абстрактні. Сюжетні задачі, пов’язані з поняттям площі є лише складені. На нашу думку, перед тим, як опрацьовувати складені задачі, доцільно ввести кілька простих сюжетних задач. Частину цих задач можна розв’язати під час усних обчислень.

Сад має форму прямокутника. Довжина саду 20 м, а його шири­на - 10 м. Чому дорівнює площа саду?

• Як знайти площу прямокутника? (Треба довжину помножити на ширину.) Якою дією розв’яжемо задачу? (Дією множення.)

Мама посадила цибулю на прямокутній ділянці площею 18 м². Ширина ділянки 3 м. Яка довжина ділянки?

Один із варіантів розбору задачі.

• Позначимо невідому довжину ділянки через х. Як тепер за допомогою рівняння можна записати її площу? (х • 3 = 18.) Я компонент у рівнянні невідомий? (Множник.) Як знайти невідомий мий множник? (Треба добуток поділити на відомий множник). Як розв’яжемо рівняння? (х = 18 : 3; х — 6.) Якою дією треба шукати сторону прямокутника? (Дією ділення. Треба площу поділити на довжину відомої сторони.)

Щоб перевірити правильність розв’язку, доцільно скласти і розв’язати обернену задачу на знаходження площі ділянки.