Задачі на різницеве порівняння чисел і і II виду

Відмінність у цих видах задач несуттєва, вона криється у фор­мулюванні запитання. Наприклад:

1. У класі 10 дівчаток і 8 хлопчиків. На скільки більше дівчаток у класі, ніж хлопчиків? (Перший вид.)

2. У класі 10 дівчаток і 8 хлопчиків. На скільки менше хлопчиків у класі, ніж дівчаток? (Другий вид.)

Короткий запис може мати такий вигляд:

Д івчаток -10

На ? більше (менше)

Хлопчиків - 8

Дужка з двома стрілками, напрямленими на числа 10 і 8, під­казує, що ці два числа треба порівняти.

На підготовчому ступені діти з’ясовують, у чому полягає порівняння двох чисел, а також ознайомлюються з подвійним змістом процесу порівняння.

Учитель викладає два ряди кружечків:

- Скільки кружечків у першому ряду? (7.) У другому? (9.) Що можна сказати про другий ряд порівняно з першим? (У другому ряду на 2 кружечки більше, ніж у першому.) Чому? (Бо в другому кружечків стільки ж, скільки у першому, і ще 2.) А що можна ска­зати про кружечки першого ряду порівняно з другим? (їх на 2 мен­ше.) Чому? (Бо в першому ряду не вистачає 2 кружечків, щоб їх було стільки, скільки у другому ряду.) Отже, якщо у другому ряду кружечків на 2 більше, ніж у першому, то в першому - на 2 мен­ше, ніж у другому. Якщо кружечки викладені ось так у два ряди, то це можна відразу побачити. Як? (У другому ряду 2 кружечки не мають пари.) А зараз я ті самі кружечки розкладу по-іншому:

Чи тепер видно відразу, на скільки більше кружечків справа ніж зліва? (Ні.) А чи не можна про де дізнатися, не викладаючи їх у ряди? (Можна. Треба полічити кружечки, дістанемо числа 7 і 9, а тоді від 9 відняти 7, буде 2.) Що означає число 2 ? (На стільки справа кружечків більше, ніж зліва.) А ще що? (На стільки зліва кружечків менше, ніж справа.) Отже, як дізнатися на скільки одне число більше, ніж друге? (Треба від більшого числа відняти менше.) А як дізнатися, на скільки одне число менше ніж друге? (Треба від більшого числа відняти менше.) Ви бачите неважливо, як запитують: «На скільки більше...?» чи «На скільки менше...?», в обох випадках дію виконують однаково: від більшого числа віднімають менше.

Таким чином, ми познайомилися із правилом порівняння /і чисел: щоб дізнатися, на скільки одне число більше або менше другого, потрібно від більшого числа відняти менше.

У підручнику для 1 класу це правило не сформульовано, вважається, що шестиліткам його ще важко прочитати і вивчити. Наслідки такого підходу свідчать, що багато дітей плутають задачі на різницеве порівняння із задачами на збільшення (зменшення) числа на кілька одиниць, а пізніше - із задачами на кратне порівняння чисел. На нашу думку, вчитель повинен звернути на це правило особливу увагу, домогтися принаймні, щоб діти могли сформулювати хоча б висновок з цього правила. Тобто, на запитання: «Як дізнатися, на скільки одне число більше від другого?» діти мають відповісти: «Потрібно від більшого числа відняти менше». Під час розбору перших задач на різницеве порівняні чисел важливо говорити дітям, що у задачі відомо два числа, які потрібно порівняти. А правило порівняння і слугуватиме обґрунтуванням вибору дії.

Розглянемо роботу над конкретними задачами на ступені ознайомлення із задачами даного виду.

У саду росло 9 яблунь і 5 груш. На скільки більше яблунь, ніж груш, росло в саду?

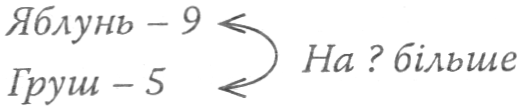
Після повторення змісту задачі вчитель говорить:

— У задачі відомо два числа — 9 і 5. Яка вимога задачі щодо цих чисел? Або: Що потрібно зробити з цими числами? (їх потрібно порівняти.) Коли запитують, на скільки більше чи менше..., це означає, що числа треба порівняти. А як дізнатися, на скільки одне число більше, ніж друге? (Треба від більшого числа відняти менше.) Якою дією розв’яжемо задачу? (Дією віднімання.) Довжина пояса 9 дм, а шарфа -19 дм. На скільки дециметрів пояс коротший, ніж шарф?

У першій задачі порівнювалися чисельності множин, а в другій - величини. Задачі на порівняння величин, особливо маси, міст­кості, площі, часу є важчими, оскільки величини складніше уяви­ти і проілюструвати. А в запитанні замість традиційного на скіль­ки більше (менше) з’являються формулювання: на скільки важче (легше), на скільки довше (коротше) та ін., які треба додатково роз’яснювати. Тому задачі з величинами у підручнику з’являються і пізніше, коли діти вже мають деякі навички розв’язувати легші задачі даного виду.

Короткий запис до задачі про пояс і шарф можна подати як у вигляді звичайного структурного запису, так і у вигляді креслення: Креслення може бути і більш наочним, якщо учитель хоче дати дітям підказку:

Обґрунтування вибору дії у цій задачі можна провести у ви­гляді наступної бесіди.

- Яку вимогу ставить задача щодо чисел 9 дм і 19 дм? (їх треба порівняти.) Що означають слова «на скільки коротший?» («На скільки менша його довжина».) А як дізнатися, на скільки одне число менше від другого? (Треба від більшого числа від менше.) Якою дією розв’яжемо задачу? (Дією віднімання.)

На третьому ступені роботи над задачами даного виду треба узагальнити спосіб їх розв’язування, домогтися, щоб учні не плутали їх із задачами інших видів. Адже часто зі словом «більше» пов’язують дію додавання, а зі словом «менше» - дію відніме Для кращого усвідомлення структури задач даного виду доці пропонувати їх у парі із задачами інших видів. Подаємо зразки таких пар, що розв’язуються як однією дією, так і різними.

1. В одному кошику 7 кг винограду, а в другому - на 2 кг більше. Скільки кілограмів винограду у другому кошику?

2. В одному кошику 7 кг винограду, а в другому - 2 кг. На скільки більше кілограмів винограду у першому кошику, ніжу другому? (Або: на скільки важчий перший кошик, ніж другий?)

1. У відро налили 8 л молока, а в каструлю – на З л менше. Скільки літрів молока налили в каструлю?

2. У відро налили 8 л молока, а в каструлю – З л. На скільки менше літрів молока налили в каструлю, ніжу відро?

1. Альбом коштує 9 грн., а блокнот - 4 грн. На скільки гривень більше коштує альбом, ніж блокнот? (Або: на скільки до­рожчий альбом, ніж блокнот?)

2. Альбом коштує 9 грн., а блокнот - 4 грн. На скільки гривень менше кошту є блокнот, ніж альбом? (Або: на скільки дешев­ший блокнот, ніж альбом?)

Під час індивідуальної допомоги слабшим учням учитель намагається, щоб учень пояснив, на основі якого правила він вибрав ту чи іншу дію.