ПЕРЕДМОВА

Зниження в Україні рівня математичної освіти в останні роки наводить на думку, що молоді вчителі-початківці поряд із соціаль­ними проблемами мають труднощі ще й професійного характеру: недостатню методичну підготовку для роботи у школі, незнання психології сприйняття математичного матеріалу молодшими шко­лярами.

Навчання розв’язувати задачі е чи не найважчим на уроках математики. Щоб воно було успішним, учитель повинен від най­першої задачі правильно вести методичну роботу: розвивати уяву учнів, диференціювати роботу над задачами, правильно проводи­ти розбір задач. Робота над складеними задачами не увінчається успіхом, якщо неправильно працювати над простими задачами — опускати обґрунтування вибору дії у них або нечітко їх ілюст­рувати. Робота над простими і складеними задачами має багато важливих нюансів. Вони є надбанням не одного покоління класоводів-практиків, проте не завжди мали належне висвітлення на сторінках методичної літератури.

Метою цього посібника є докладне висвітлення методичних при­йомів роботи над математичними задачами у початкових класах. Оскільки автор цієї книжки мав честь багато років спілкуватися і співпрацювати з М. Богдановичем, автором чинних підручників з математики для 1-4 класів, даний посібник базується переважно на системі задач його підручників. Проте деякі оригінальні задачі розглянуто і з підручника Л. Кочиної, Н. Листопад.

На початку описано основні питання загальної методики ро­боти над задачами, а далі подано розгляд практичних підходів до опрацювання простих і складених задач за роками навчання.

Аналізуючи систему задач у кожному класі, автор намагається розбити її на групи і підгрупи, зручні для опрацювання, а далі по­дає методику роботи над кожною групою. У тексті є посилання на номери задач підручників, які описуються в даний момент (і в яких змінено сюжет або числові дані).

Посібник буде корисний і студентам педагогічних факультетів під час вивчення методики викладання математики і проходжен­ня педагогічної практики в початкових класах, а також батькам молодших школярів, які не байдужі до якості математичної осві­ти своїх дітей.

Розділ 1. ЗАГАЛЬНІ ПИТАННЯ МЕТОДИКИ

ОПРАЦЮВАННЯ ЗАДАЧ. ПРОСТІ ЗАДАЧІ

СТУПЕНІ ТА ЕТАПИ РОБОТИ НАД ТЕКСТОВОЮ ЗАДАЧЕЮ

У посібнику подано прості й ефективні способи роботи над арифметичними текстовими задачами у початкових класах. Ариф­метичною називається та задача, в якій ставиться вимога обчис­лити значення деякої величини за відомими числовими значення­ми інших величин і існує залежність, яка пов’язує ці величини як між собою, так і з шуканою. Текстовою називається задача, умову і вимогу якої сформульовано словесно, у вигляді тексту - розповідних та питальних речень. Текстові задачі поділяють на сюжетні й абстрактні. Зміст сюжетної задачі відображає якусь життєву ситуацію, абстрактні ж задачі у початкових класах пе­реважно є задачами про абстрактні числа.

Серед багатьох функцій, що їх виконують задачі у навчанні математики молодших школярів, найважливішою є розвивальна функція, спрямована на оволодіння прийомами розумової діяль­ності. Від того, як дитина мислить, залежить її подальше життя, вибір професії, вміння знайти вихід у складній життєвій ситуації. Нація, що мислить повноцінно, конструктивно, є запорукою ус­пішної розбудови держави. Можна без перебільшення сказати, що майбутнє держави і доля конкретної людини перебувають у руках вчителів початкових класів. Багато залежить від того, яку основу закладено для розвитку дітей, чи вдалося вчителеві зацікавити учнів корисними видами діяльності, підготувати їх до життя у суспільстві. Арифметична задача має великі можливості для цьо­го, адже вона відображає конкретну життєву ситуацію, міні-проблему, з якої треба навчитися знаходити вихід. Некомпетентність чи байдужість учителя початкових класів дорого обходиться су­спільству, адже прогалини у розвитку мислення дитини, як пра­вило, не можна надолужити у зрілому віці. Невміння розв’язувати прості задачі призводить до нездатності розуміти в майбутньому не лише задачі з математики, а й з фізики, хімії, біології тощо.

Успішне навчання розв’язувати задачі можливе лише за умови, що з найпершої задачі методика роботи вчителя є повноцінною.

Учень лише тоді може розв’язати задачу, коли він здатний уя­вити собі ситуацію, що її в ній описано. Розвинена уява допомагає відшукати приховані зв’язки між даними і шуканими величина­ми. Навчити дитину уявляти можна за допомогою правильного ілюстрування задачі. Спочатку ілюстрація повинна бути якомога наочнішою: оперування лічильним матеріалом, практичне від­творення конкретної ситуації (задачі на рух), предметні малюнки тощо. З часом учень навчиться ці маніпуляції виконувати уявно і тоді ілюстрації до задачі можна буде здійснювати абстрактніше: у формі структурного запису, креслення чи таблиці, тобто коротко­го запису змісту задачі.

Успіх у роботі над задачами великою мірою залежить від наявності у підручнику системи задач, у якій продумана кількість і чергування задач одного і різних видів. Система задач, пропонова­на у чинних підручниках з математики, не завжди забезпечує пов­ноцінне навчання учнів, тому вчитель повинен бачити її недоліки і вміти їх нейтралізувати своєчасним доповненням відповідних задач з інших джерел.

Навчання розв’язувати задачі даного виду здійснюється за трьо­ма ступенями методичної роботи.

Перший ступінь - підготовчий. Він готує учнів до усвідом­лення сутності арифметичних дій, знайомить з величинами і зв’язками між ними. Робота над задачами на цьому ступені буде докладно розкрита під час опису конкретної методики роботи над кожним видом задач.

На другому ступені учні вперше знайомляться із задачею даного виду та способами її розв’язування. Робота проходить у чотири етапи: ознайомлення зі змістом задачі; відшукання спо­собу розв’язування; розв’язування задачі; перевірка розв’язання та формулювання відповіді. Ми не ставимо своїм завданням до­кладно описувати кожний етап, бо це зроблено в усіх підручниках з методики викладання математики в початкових класах. Обмежи­мося лише кількома заувагами. Від якості роботи на першому ета­пі залежить подальший успіх роботи над задачею. Учитель повинен домогтися, щоб учні добре усвідомили зміст задачі. Короткий запис доцільно виконувати поступово, у ході бесіди, що розкриває умову і запитання. У цьому разі діти будуть розуміти структуру запису, зможуть скористатися ним під час другого етапу - відшукання способів розв’язування задачі.

Відшукання способів розв’язування задачі можна здійснювати як від числових даних до запитання, так і від запитання до чис­лових даних. Кожен зі способів має свої переваги і недоліки. Роз­бір від числових даних до запитання подається у такому вигляді: якщо нам відомо □ і □, то про що за цими даними можна дізнати­ся? Запитання у такій формі тривають доти, доки розбір не дійде до основного запитання задачі. Вчитель сам вибирає послідовність виконання дій, тому цей спосіб сприяє швидшому розв’язуванню задачі. Проте учні при цьому пасивно стежать за думкою вчителя. Спосіб від запитання до числових даних є складнішим, потребує більше часу, однак учні мають можливість самі вибрати послідов­ність дій, а вчитель лише спрямовує їх на правильний шлях. За­питання вчителя мають такий вигляд: чи можемо ми відразу дати відповідь на запитання задачі? Які дві величини для цього потріб­но мати? Що нам з цих двох величин відомо, а що невідомо? Чи можемо ми знайти невідому величину? Чому? І т. д. Робота над задачами на другому етапі докладно буде висвітлена далі.

Другий етап роботи над задачею є найвідповідальнішим. Якщо він проведений якісно, то саме розв’язування задачі і формулю­вання відповіді не повинні становити труднощів для більшості учнів класу. Однією із ознак неякісної роботи на другому етапі є «змішування» другого і третього етапів. Особливо воно поширене під час розбору задачі від числових даних до запитання. Учитель запитує:

« Якщо нам відомо ... і ..., то про що ми можемо дізнати­ся за цими даними? (Відповіді учнів.) Як ми про це дізнаємося? Запишіть першу дію. А тепер, коли ми вже знаємо ... і з умови ві­домо ..., то що за цими двома даними можна дізнатися? Як ми це дізнаємося? Запишіть другу дію». Такий стиль роботи дуже конк­ретний, тому задача розв’язується швидко і легко. Здавалось би, чого ще треба? А треба, щоб учень вчився самостійно міркувати, інакше робота втрачає сенс. А щоб він міркував, потрібно вчити його бачити абстрактну структуру задачі, незалежно від чисел і сюжету. Абстрагування від конкретного змісту задачі не може ви­робитись, якщо у процес міркування весь час «вплутують» числа. Якщо постійно проводити абстрактний розбір задачі, то учень на підході до третього етапу вже уявляє структуру розв’язання, на­приклад, таку: * - * .

Таке мислення дасть йому можливість в майбутньому впізнати цю структуру в задачі того самого виду з будь-якими сюжетними і числовими даними.

Тільки по завершенні розбору задачі на другому етапі вчитель дозволяє переходити до третього етапу — розв’язування задачі.

Деякі вчителі практикують роботу на третьому етапі у такий спосіб: один учень виходить до дошки і записує розв’язання задачі за допомогою арифметичних дій, виразу чи рівняння. Зловживан­ня цим способом призводить до того, що учні не мають стимулу сумлінно працювати над задачею на першому і другому етапах, бо впевнені, що можуть переписати у зошити готове розв’язання.

Щодо перевірки правильності отриманого розв’язку (четвер­тий етап), то загальні її способи докладно описані у підручниках з методики. Під час опису роботи над конкретними видами задач ми подамо деякі з них.

На третьому ступені роботи над задачами даного виду вчи­тель закріплює вміння їх розв’язувати. Учні повинні навчитися розв’язувати будь-яку задачу розглядуваного виду незалежно від її конкретного змісту. Тобто вони повинні впізнавати структуру задач даного виду серед задач інших видів і узагальнити спосіб їх розв’язування. На третьому ступені робота над задачею не вимагає такої докладності, як на другому. Так, ознайомлення зі змістом задачі учні здійснюють самостійно. Після того як вони прочитали задачу, вчитель пропонує одному учневі переказати її. Відповідь учня продемонструє, чи зрозумів він зміст задачі, чи ні. Розбір за­дачі має тенденцію до скорочення, а розв’язування доцільно вико­нувати з усе більшим ступенем самостійності учнів. Цьому сприяє організація диференційованої роботи над задачею, творчої роботи над уже розв’язаною задачею, подача задач різних видів, але з подібним сюжетом парами і трійками тощо.

Таким чином, робота над задачами кожного виду вкладається у схему :

		III ступінь Закріплення вмінь розв’язувати задачі даного виду
	II ступінь Ознайомлення із задачею даного виду
	І етап | II етап | III етап | IV етап
І ступінь Підготовчий

Перейдемо до опису методики роботи над конкретними видами задач.

Прості задачі Класифікація видів простих задач і їх розподіл за роками навчання

Простою називають задачу, для розв’язування якої треба ви­конати одну арифметичну дію. Задачу, для розв’язування якої треба виконати дві чи більше пов’язаних між собою арифметич­них дій, називають складеною. Будь-яку складену задачу можна розбити на кілька простих, тому вміння розв’язувати складені за­дачі залежить від уміння розв’язувати прості задачі.

Більшість видів простих задач, що їх вивчають у початкових класах, можна поділити на три основні групи.

До першої групи належать прості задачі, під час розв’язування яких учні засвоюють конкретний зміст кожної з арифметичних дій. Це задачі на знаходження: суми двох чисел; остачі; суми од­накових доданків (добутку); частки (ділення на рівні частини і ділення на вміщення).

До другої групи відносять прості задачі, під час розв’язування яких учні засвоюють зв’язки між компонентами і результатами арифметичних дій. Це задачі на знаходження невідомих компо­нентів: доданка, зменшуваного, від’ємника, множника, діленого, дільника.

До третьої групи належать задачі, пов’язані з поняттям різнице­вого чи кратного відношення двох чисел. Це задачі на збільшення чи зменшення числа на кілька одиниць або в кілька разів (у прямій і непрямій формі), на різницеве чи кратне порівняння двох чисел.

Крім вищеописаних груп задач, у початкових класах розгляда­ють ще декілька видів простих задач: задачі на час, на обчислення площі прямокутника, на знаходження частини числа та числа за його відомою частиною та ін.

Розглянемо розподіл простих задач за роками навчання.

1 клас

1. Знаходження суми двох чисел.

2. Знаходження остачі.

3. Збільшення та зменшення числа на кілька одиниць (пряма форма).

4. Різницеве порівняння двох чисел.

5. Знаходження невідомого доданка.

2. клас

1. Знаходження невідомого зменшуваного,

2. Знаходження невідомого від’ємника.

3. Знаходження суми однакових доданків.

4. Знаходження частки (ділення на рівні частини).

5. Знаходження частки (ділення на вміщення).

6. Знаходження частини числа.

7. Збільшення та зменшення числа у кілька разів (пряма форма).

2. клас

1. Кратне порівняння двох чисел.

2. Знаходження невідомого множника.

3. Знаходження невідомого діленого.

4. Знаходження невідомого дільника.

5. Задачі на ділення з остачею.

6. Знаходження числа за його відомою частиною.

2. клас

1. Збільшення та зменшення числа на кілька одиниць у непря­мій формі.

2. Збільшення та зменшення числа у кілька разів у непрямій формі.

3. Знаходження площі прямокутника.

4. Задачі на час: визначення тривалості події; початку події; закінчення події.

5. Прості задачі на подвійне різницеве відношення.

Методика опрацювання простих задач

Кожний вид простих задач має певну специфіку опрацюван­ня. Нехтування цією специфікою якраз і є причиною невміння розв’язувати задачі, невміння функціонально мислити у майбут­ньому. Нагадаємо, що кожний вид задач потребує триступеневої методичної роботи, а на другому ступені - чотирьох етапів ро­боти над задачею. Деякі вчителі, ознайомлюючи із новим видом простої задачі, опускають найважливіший другий етап - відшу­кання способів розв’язування задачі. Якщо задача розв’язується однією арифметичною дією, то розбір від запитання чи від число­вих даних втрачає сенс. Тому після повторення змісту задачі вчи­тель запитує: «Якою дією розв’яжемо задачу?» Оце і є початком подальших невдач для багатьох учнів. Що відбувається у класі при такому «розборі»? Сильніші учні відразу правильно назива­ють дію. Але в цьому немає заслуги вчителя. Такі учні мають природні здібності до свідомого вибору дії. Вони можуть і без вчителя розв’язати задачу. Решта учнів класу пасивно сприймає готову відповідь товариша і не має змоги самостійно подумати над вибором дії. Що залишається робити таким учням під час розв’язування домашнього завдання? Чекати підказки дорослих або відгадувати розв’язання. Однак задача не загадка, вона потре­бує осмислення.

Відшукання способів розв’язування простої задачі має свою специфіку - воно зводиться до обґрунтування вибору дії. Як уже було сказано, це обґрунтування спочатку здійснюється на основі практичного оперування ілюстративним матеріалом, а згодом таке оперування здійснюється в уяві дітей. Деякі види простих задач розв’язуються на основі згадування відповідних математичних правил. Розглядаючи конкретну методичну роботу над задачами кожного виду, особливу увагу ми звертатимемо саме на обґрунту­вання вибору арифметичної дії.

Перша група простих задач - задачі на розкриття конкретного змісту кожної з арифметичних дій

Задачі на знаходження суми двох чисел

1. На подвір’ї клювали зерно б курей. До них прибігли ще З курки. Скільки всього курей стало на подвір’ї?

2. У коробці було 2 простих і 7 кольорових олівців. Скільки всього олівців було в коробці?

3. З автостоянки від’їхало 8 легкових автомобілів і 2 вантаж­них. Скільки всього автомобілів від’їхало з автостоянки?

Цей вид уперше знайомить учнів з поняттям «задача». Він роз­криває конкретний зміст дії додавання. Сутність його полягає в тому, що є дві множини предметів, чисельність кожної відома. Ці множини об’єднують в одну множину, чисельність якої потріб­но знайти. Тому на першому, підготовчому, ступені роботи над цим видом задач діти вчаться об’єднувати множини і перелічува­ти результат. Після вивчення чисел першої п’ятірки вони знайом­ляться зі знаками “=”. Це дає змогу результат об’єднання множин записувати прикладом. Вправи на підготовчому ступені можуть бути такими:

1. Покладіть зліва 4 палички, а справа - 2. Скільки всього пали­чок ви поклали?

Учні зсувають палички докупи, перелічують їх і записують приклад: 4 + 2 = 6.

2. Дівчинка засушила 5 жовтих і 4 зелених листки. Скільки всьо­го листків засушила дівчинка?

Учитель викладає на набірному полотні відповідну кількість жовтих і зелених листків. Учні в цей час на партах оперують лі­чильним матеріалом: якщо немає вирізаних з паперу листків, їх заміняють кружечками, трикутниками чи паличками.

Виконавши достатню кількість таких вправ, діти усвідом­люють, що дія додавання виконується тоді, коли дві множини об’єднуються в одну більшу. Тому і результат виходить завжди більший, ніж числа, які додавали.

Другий ступінь, тобто ознайомлення із задачею на знаход­ження суми, починається після ознайомлення з числом 0. Учи­тель здійснює знайоме дітям об’єднання множин, проте результат новоутвореної множини перелічити не можна.

Оленка знайшла 5 лисичок і 3 маслючки. Скільки всього грибів знайшла Оленка?

Учитель кладе у кошик спочатку 5 грибів, потім 3, але уч­ням не видно, скільки грибів стало в кошику. Знайома ситуація наштовхує дітей на думку, що розв’язання задачі треба записати дією додавання: 5 + 3 = □.

Проте вчитель не може розраховувати на те, що всі діти це зрозуміли. Тому важливо на перших порах проводити бесіду, яка і є обґрунтуванням вибору дії додавання.

- Коли до 5 лисичок я кладу ще 3 маслючки, то у кошику стає грибів більше чи менше, ніж було спочатку? (Більше.) А якщо стало більше, то якою дією запишемо розв’язання? (Дією дода­вання.) Учитель записує на дошці, а учні - в зошитах приклад 5 + 3. Відповідь учні не можуть перелічити, тому результат вони шукають у таблиці додавання числа 3, а після вивчення таблиці напам’ять відразу зможуть записати відповідь.

Якщо дитина сумнівається, яку дію треба вибрати, то і на другому ступені вчитель дозволяє їй скористатися лічильним ма­теріалом.

Поступово ілюстрування лічильним матеріалом заміню­ють більш абстрактним коротким записом:

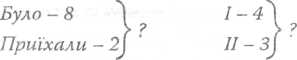Було - 4

Прилетіло - 5

Стало - ?

Такі записи учитель може використовувати лише тоді, коли учні навчаться читати.

Задачі на знаходження остачі

1. На гілці сиділо 6 горобців. 2 горобці полетіли. Скільки горобців залишилося на гілці?

2. В Олі було 8 зошитів. З зошити вона подарувала братові. Скільки зошитів залишилося в Олі?

3. Білочка знайшла 9 горішків. 2 горішки вона загубила. Скільки горішків залишилося в білочки?

Підготовчі вправи починаються ще під час вивчення нумерації чисел першого десятка. Вони полягають у вилученні із множини її правильної частини і перелічуванні елементів, які залишилися. Наприклад, скориставшись змістом першої задачі, можна викона­ти таку вправу.

- Покладіть стільки паличок, скільки горобців було на гілці спочатку. (Діти викладають 6 паличок.) Що треба зробити, щоб показати, що 2 горобці полетіли? (Діти забирають 2 палички.) Скільки паличок залишилося? (4.) Що вони означають? (На гілці залишилося 4 горобці.) Після введення знака у кінці вивчення чисел першого десятка учні можуть записувати результат прикла­дом на віднімання.

Ознайомлення із задачею на знаходження остачі (другий ступінь) відбувається на тому самому уроці, коли діти знайом­ляться із задачею на знаходження суми. Обидві задачі розгля­дають паралельно. Так само, як і в задачі на знаходження суми, результат вилучення підмножини діти не можуть перелічити. Але виконавши на попередніх уроках достатню кількість вправ на вилучення підмножини, вони впізнають знайому ситуацію і пра­вильно вибирають дію. Проте, як і під час роботи над задачею на знаходження суми, обґрунтувати вибір необхідно.

- Коли 2 горобці полетіли, на гілці їх стало більше чи мен­ше, ніж було спочатку? (Менше.) А якщо менше, то якою дією розв’яжемо задачу? (Дією віднімання.) Учні записують у зошитах приклад на віднімання. Оскільки перелічити результат не можна, відповідь вони знаходять у таблиці віднімання числа 2. Згодом вони знатимуть таблицю напам’ять і такі обчислення не виклика­тимуть труднощів.

Необхідно зауважити, що слабші діти потребують тривалішо­го оперування лічильним матеріалом. їм потрібно, як і під час підготовчої роботи, об’єднувати палички і вилучати їх частину та перелічувати результат. Учитель не повинен «підганяти» таких дітей, бо у них ще не сформувався перехід від наочного споглядан­ня до уявного оперування множинами. Для такої дитини важливе не швидке просування далі з усіма учнями, а усвідомлення, як можна самостійно зарадити собі в кожній задачній ситуації, як за допомогою лічильного матеріалу моделювати ситуацію і знайти відповідь на запитання задачі. Лише тоді, коли дитина буде впев­нена, що в кожній задачі вона здатна сама розібратися, що є на те зручний спосіб - опора на наочність, вона матиме впевненість, що математичні премудрості їй під силу, що вона сама може з ними впоратися. Тільки в такому разі у дитини з’явиться установка, що треба самостійно шукати розв’язання, а не чекати готової під­казки. Розв’язуючи такі задачі самостійно, діти доти мають право користуватися лічильним матеріалом, поки не зможуть робити це уявно. Поступово предметне ілюстрування вчитель замінює ко­ротким записом, який може мати різний вигляд:

а) структурний запис; б) таблиця; в) креслення.

а) Було - 10 ябл.

Віддали - 4 ябл.

Залишилося - ?

Було	Відрізали	Залишилося
18 м	6 м	?

б)

в)

На третьому ступені (закріплення вмінь розв’язувати задачі даного виду) учні повинні навчитися розпізнавати вид задачі і правильно вибирати дію. Для цього задачі на знаходження суми і остачі у підручнику подають почергово. Часто на одному уроці учні розв’язують пари або трійки задач з подібним сюжетом. Учи­тель не повинен обмежуватися лише добіркою задач підручника. Він може складати такі задачі і самостійно. Не обов’язково запи­сувати всі розв’язання у зошити, частину задач можна розв’язати й усно.

Розглянемо зразки роботи над парами і трійками задач.

1. В Ігоря було 7марок. Тато подарував йому ще 3 марки. Скільки марок стало в Ігоря?

2. В Ігоря було 7 марок. З марки він подарував татові. Скільки марок стало в Ігоря?

Обґрунтування вибору дій у цих задачах має такий вигляд.

— Коли тато подарував Ігорю 3 марки, у нього стало марок біль­ше чи менше, ніж було спочатку? (Більше.) Якою дією розв’яжемо задачу? (Дією додавання.)

Коли Ігор подарував 3 марки татові, у нього стало марок біль­ше чи менше, ніж було спочатку? (Менше.) Якою дією розв’яжемо задачу? (Дією віднімання.)

Доцільно провести з учнями узагальнювальну бесіду про так звані визначальні слова у змісті задачі. Ці слова визначають ариф­метичну дію, якою розв’язується задача. Часто діти помилково вважають слова приїхали, подарували, принесли, прилетіли таки­ми, що визначають дію додавання, а слова відлетіли, від’їхали, віддали, пішли - визначальними для дії віднімання. Це непра­вильно, бо не завжди спрацьовує. Визначальні для дії додавання і віднімання слова криються у запитанні задачі. Якщо запитується «Скільки всього...», «Скільки разом...», то саме слова всього чи разом вказують на об’єднання множин, а отже, і на дію додаван­ня. Якщо ж запитується «Скільки ... залишилося...», то слово залишилося визначає дію віднімання, бо передбачає знайти решту після вилучення підмножини. Однак у деяких задачах визначаль­ні слова спеціально опускаються або замінюються іншими, щоб ускладнити пошук дії. Так, у наведеній парі задач запитання зву­чать однаково: «Скільки марок стало в Ігоря?» Учні самі повинні здогадатися, що запитання першої задачі можна перефразувати так: «Скільки всього марок стало в Ігоря?», а запитання другої – «Скільки марок залишилося в Ігоря?» Як бачимо, розгляд задач парами підсилює методичний ефект, дає можливість учням порів­нювати та узагальнювати розв’язання відразу двох видів задач.

Наведемо ще кілька зразків таких груп задач.

1. У магазин привезли 20 кг зефіру. До обіду продали 12 кг, а решту - після обіду. Скільки кілограмів зефіру продали після обіду?

2. У магазин привезли зефір. До обіду продали 20 кг, а після обіду - 12 кг. Скільки кілограмів зефіру продали?

1. У туристському таборі було 15 пішохідних туристів. До них приїхало ще 8 туристів на велосипедах. Скільки туристів стало в таборі?

2. У туристському таборі було 15 туристів. 8 з них приїхали на велосипедах, а решта - прийшли пішки. Скільки пішохідних туристів було в таборі?

3. Із туристського табору пішли на екскурсію 15 туристів, а 8 - поїхали на велосипедах. Скільки туристів залишили табір?

Кожна група задач потребує узагальнювальної бесіди, під час якої діти повинні з’ясувати, які слова визначають дію задачі і чи включені вони в її формулювання, чи ні; а також назвати слова, які помилково можна прийняти за визначальні. Так, у запитанні останньої задачі слово «залишили» може хибно наштовхнути на вибір дії віднімання. Насправді визначальним тут є слово «всьо­го», яке в запитанні опущено.

Задачі на знаходження суми однакових доданків (добутку)

Підготовчі вправи до цього виду задач одночасно ознайомлю­ють дітей із третьою арифметичною дією. Тому вони є першими у темі «Множення» у 2 класі.

Ці вправи можуть мати такий зміст:

Скільки всього жолудів ?

Діти звично об’єднують множини і розв’язують таку задач дією додавання, але щоразу переконуються, що і об’єднання, і до давання мають свою особливість: усі множини є рівночисельними а тому суму записують за допомогою однакових доданків, яких час то буває більше, ніж два, тому приклад виходить довгим. Учитель підводить дітей до думки, що не завжди такий приклад зручно ч навіть практично можливо записати. Наприклад, як записати і об числити грошову суму, якщо є сто монет по 5 копійок? У такий спосіб учитель обґрунтовує необхідність введення способу записати цю суму коротше, тобто доцільність введення нової арифметичної дії — множення. Множення - це сума однакових доданків, яку записують за допомогою лише двох компонентів: перший показує доданок, що повторюється, а другий визначає, скільки разів він повторюється. Деякі методисти вважають, що неважливо, на якому місці записати «доданок», а на якому – «рази», адже, мовляв, від перестановки множників добуток не змінюється. На нашу думку цей порядок дуже важливий, оскільки саме він вже на початках допоможе учням включити уяву, яка у кожній конкретній задачі непомильно вкаже, що треба виконати об’єднання множин, отже, розв’язати задачу множенням (а не діленням). Для того щоб ця уява запрацювала, треба багато разів за допомогою роздаткового матеріалу виконати таке об’єднання, записати суму однакових доданків, а тоді замінити її прикладом на множення; і навпаки, приклад на множення замінити прикладом на додавання.

Під час ознайомлення із задачами нового виду (другий ступінь) умова задачі нерідко формулюється так, що спочатку називається число, яке означає другий множник. Наприклад: «Шістьом кро­лям дали по 2 морквини. Скільки всього морквин роздали?» Якщо учень мислить правильно, то уява малює йому 2 морквини, ще 2 морквини, ще 2 морквини, і так 6 разів. Він розуміє, що додава­ти треба морквини, а не кролів, вміє записати приклад на додаван­ня, а з нього утворити приклад на множення: 2-6 = 12, і пояснити, що означає у ньому кожне число. Якщо ж учень пише 6-2 = 12, то це сигнал вчителеві, що уява його не працює і він дію вибрав ме­ханічно. Поки немає задач на ділення, шкода від цього нібито неве­лика. Але коли з’являться задачі на ділення, учень з таким самим успіхом може написати розв’язання даної задачі дією ділення - 6:2 = 3, адже він не уявляє, чи об’єднуються тут множини, чи множина ділиться на рівночисельні підмножини.

Задачі на ділення на рівні частини і на вміщення

Підготовчі вправи до задач на ділення на рівні частини слугу­ють одночасно для ознайомлення з дією ділення, яка вводиться піс­ля вивчення таблиці множення числа 2. Це вправи на практичний поділ множини на рівні частини. Вчитель може запропонувати уч­ням завдання: треба 15 зошитів роздати порівну трьом учням. По скільки зошитів дістане кожен учень? Як виконати такий поділ, щоб не помилитися? Треба роздавати зошити по одному, поки не вичерпаються усі, і після цього подивитися, скільки зошитів дістав кожний учень, чи порівну розподілено зошити. Як запи­сати приклад розв’язання цієї вправи? Зошитів було 15, учитель записує на дошці число 15. їх розділили порівну між трьома уч­нями - пропустивши місце для знака дії, вчитель записує число 3. Яку дістали відповідь? Кожний учень одержав 5 зошитів. Учитель записує знак “=” і число 5. Одержали запис: 15 3 = 5. Бракує лише знака дії. Учні переконуються, що жодна з трьох раніше вивчених дій тут не підходить. Тому є потреба познайомитися з четвертою арифметичною дією.

- Що ми робили з зошитами? (Ділиш їх порівну на 3 части­ни.) Тому і дія називається ділення та позначається знаком

Учитель вписує його в приклад і вчить читати: 15 поділити на З, буде 5.

Ознайомлення із сюжетними задачами на ділення відбуваєть­ся під час розв’язування задач на знаходження добутку, тому учні відразу повинні уявляти, що відбувається з множинами: об’єднання чи поділ на рівні частини. Дуже швидко вводиться й останній вид цієї групи задач - ділення на вміщення.

Задача на ділення на вміщення у підручнику з самого початку протиставляється задачі на ділення на рівні частини.

Учитель роздав 15 зошитів кільком учням, по 3 зошити кожно­му. Скільком учням роздано зошити?

Учні бачать, що розв’язання задач записується однаково, а відрізняється лише формулювання відповіді. Щоб відрізнити одну задачу від другої, вчителі вчать читати приклади по-різному: 15 поділити на 3 і 15 поділити по 3. Щоб учні не плутали назви най­менувань, потрібно багато задач розв’язати практично, використо­вуючи роздатковий матеріал.

На третьому ступені доцільно розв’язувати задачі на мно­ження і ділення, на знаходження суми - парами і трійками, після чого проводити узагальнювальні бесіди.

Розглянемо приклади таких груп задач.

1. У 8 склянок розставили пензлики, по 2 у кожну. Скільки всього пензликів розставили?

2. У склянки розставили 8 пензликів, по 2 у кожну. Скільки знадо­билося склянок?

1. 12 листівок розклали порівну в 2 конверти. По скільки листі­вок клали у кожний конверт?

2. 12 листівок розклали у конверти, по 2 листівки в кожний. Скільки знадобилося конвертів?

1. У трьох пеналах по 2 олівці. Скільки всього олівців?

2. В одному пеналі 3 олівці, а в другому - 2. Скільки всього олів­ців?

1. У 9 ваз розставили троянди, по 3 в кожну вазу. Скільки троянд розставили?

2. 9 троянд розставили у вази, по 3 в кожну. Скільки ваз вико­ристали?

3. 9 троянд розставили порівну в 3 вази. По скільки троянд ста­вили в кожну вазу?

Як видно з умов наведених задач, без належно розвиненої уяви правильно вибрати дію складно. Тому задачі необхідно розв’язувати практично доти, доки ця уява не запрацює. Варто звернути увагу дітей і на такі закономірності: коли ми множимо, то стає більше, а коли ділимо, то стає менше.

Пізніше сюжет задач ускладнюється тим, що замість окремих предметів ідеться про величини: масу, довжину, місткість і т. д. Наприклад: “У 9 кошиків розсипали сливи, по 3 кг у кожний. Скільки кілограмів слив розсипали?” Таку задачу доцільно подати у парі з першою задачею останньої трійки. Діти побачать, що дода­нок, який повторюється (3 троянди), замінили трьома кілограмами слив. Це уявити складніше, проте структура задачі не змінилася.

Ми підійшли до важливого етапу у розв’язуванні задач: вве­дення у зміст задач трійок пов’язаних між собою величин. Наведе­мо зразки таких трійок, що зустрічаються в задачах у початкових класах: ціна, кількість і вартість; маса одного предмета, кількість таких предметів і загальна маса; місткість однієї посудини, кіль­кість таких посудин і загальна місткість; площа однієї кімнати, кількість однакових кімнат і загальна площа; тривалість одно­го уроку, кількість таких уроків і загальна тривалість; довжина одного відрізу, кількість однакових відрізів і загальна довжина; швидкість, час і відстань; продуктивність праці, час і робота.

Наведені трійки величин фігурують і в простих, і у складених задачах. Розуміння зв’язку між ними е запорукою подальшого успішного розв’язування типових задач, задач з типовим конкрет­ним сюжетом тощо.

І хоч прості задачі з цими трійками величин належать до тих самих трьох видів задач на розкриття конкретного змісту дій мно­ження і ділення, у підручниках математики вони вводяться посту­пово. Так, задачі про продуктивність праці, час і роботу - в 3 класі, а задачі про швидкість, час і відстань - у 4. Дуже важливо навчити дітей знаходити одну з цих величин за двома іншими.

Для цього варто складати трійки взаємообернених задач. На­приклад:

Задача на знаходження суми однакових доданків	Купили 3 блокноти, ціною по 2 грн. Яка вар­тість покупки?
Задача на ділення на рівні частини	За 3 однакових блокноти заплатили б грн. Яка ціна блокнота?
Задача на ділення на вміщення	На 6 грн. купили однакові блокноти, ціною по 2 грн. Скільки блокнотів купили?

Таких вправ у підручнику явно бракує, особливо з такими трійками величин, як продуктивність, час і робота; місткість од­нієї посудини, кількість посудин і загальна місткість тощо. Саме недостатня кількість розв’язаних учнями простих задач даних трьох видів є причиною подальшого нерозуміння зв’язків між ве­личинами у складених задачах.

У наступному розділі, де йтиметься про роботу над складени­ми задачами, буде показано, що короткий запис багатьох типових задач (і не лише типових) доцільніше записувати у формі таблиці, яка містить три стовпці з назвами трьох величин. Щоб підготу­вати дітей до вміння користуватися таким записом, доцільно під час розбору простих задач зазначених видів короткий запис їх виконувати час від часу у вигляді таблиці. Наприклад:

Обточує за 1 год	Кількість годин	Вся робота
8 деталей	6	?

Хочемо наголосити, що і назви трьох величин в усіх на них вище трійках, і назви стовпців таблиці найзручніше подавати в одному порядку: перший множник, другий множник, добуток. Тоді дітям легше запам’ятати, якою дією обчислюється кожна величин. Наприклад, у задачі, короткий запис якої має вигляд :

Швидкість	Час	Відстань
12 км/год	?	36 км

видно, що невідомий час є другим множником, а щоб знайти другий множник, треба добуток поділити на перший множник, ті відстань треба поділити на швидкість.

Ми розглянули особливості методики опрацювання задач першої групи, яка включає 5 видів задач на розкриття конкретного змісту арифметичних дій.

Треба додати, що на третьому ступені роботи над цими зад; ми велику користь дає творча робота над уже розв’язаною задач перетворення задачі (зміна числових даних, зміна сюжету, складання обернених задач); порівняння задач; складання нових за, (на вказану дію; за поданим виразом чи розв’язанням; на вказаний вид; за поданими числовими даними; за коротким записом).

Наприклад:

1. Складіть задачу, яка б розв’язувалася дією віднімання.

2. Складіть задачу, яка б розв’язувалася так: 7+2.

3. Складіть задачу на ділення на рівні частини.

4. Складіть задачу, у якій були б вирази: «6 книжок» і “3 портфелі»

5. Складіть задачу за коротким записом:

16 л. у 4 каструлі по ? л.

Така робота дає учневі можливість абстрагуватися від конкретного змісту задачі, бачити найсуттєвіші ознаки виду, структуру розв’язання. Особливо корисною є творча робота над складеними ї задачами, структуру яких зрозуміти найважче. Однак вона буде під силу більшості учнів класу лише тоді, якщо учитель привчав до неї дітей ще під час розв’язування простих задач.

Друга група простих задач - задачі на знаходження невідомого компонента.

Задачі на знаходження невідомого доданка, зменшуваного і від’ємника

Задачі на знаходження невідомого доданка вводять у 1 класі, а на знаходження зменшуваного і від’ємника - у 2. До третього класу такі задачі розв’язуються на основі розуміння конкретного змісту дій додавання та віднімання і зводяться до розв’язування раніше вивчених видів задач - на знаходження суми й остачі.

Тому підготовчим ступенем до введення задач на знаходжен­ня доданка, зменшуваного і від’ємника слугує розв’язування за­дач на знаходження суми й остачі.

Ознайомлення з новим видом задач супроводжується вико­нанням відповідних операцій над множинами. Розглянемо роботу над конкретними задачами.

Задача на знаходження доданка

У саду росло 5 яблунь і кілька груш, а всього 9 дерев. Скільки груш росло в саду?

- Покладіть стільки паличок, скільки всього дерев росло в саду. (9 паличок.) З яких двох частин складаються ці 9 дерев? (З яблунь і груш.) Яка з цих двох частин нам відома, а яка - не­відома? (Відомо, що було 5 яблунь, а кількість груш невідома.) Покажіть на ваших паличках яблуні. (Учитель стежить, як діти це роблять. Якщо вони із 9 паличок відсовують 5, отже, міркують правильно. А та дитина, яка дістає ще 5 паличок і кладе їх збоку, потребує індивідуальної роботи.) Що означають нерухомі палички? (Це груші, їх 4.) Як ви про це дізналися? (Ми від 9 паличок забрали 5, залишилося 4.) Якою дією розв’яжемо задачу? (Дією віднімання.) У першому класі діти ще не знайомі з правилом знаходження невідомого доданка, тому вибір дії від­бувається на основі знайомої операції над множинами. Учитель може перефразувати задачу, щоб діти побачили її зв’язок із задачею на знаходження остачі:

У саду росло 9 дерев, з них 5 - яблуні, а решта - груші. Скільки груш росло в саду?

Подивимося, як виглядала б робота над цією самою задаче; третьому ступені.

На третьому ступені діти вже не оперують паличками. Ілюстрацією структури задачі у цей період може слугувати короткий запис:

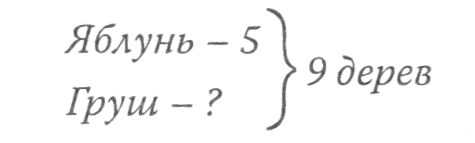
Якщо є потреба в обґрунтуванні вибору дії, то воно може бути таким:

• З яких двох частин складаються всі дерева? (З яблунь і груш.) Яка частина нам відома, а яка - невідома? (Кількість яблунь відома, а груш - ні.) Як знайти невідому частину? (Треба від усіх дерев забрати відому частину.) Якою дією розв’язується задача? (Дією віднімання.)

Задача на знаходження зменшуваного

В автобусі їхало кілька пасажирів. Коли на зупинці вийшли 4 пасажири, в автобусі залишилося 3 пасажири. Скільки паса­жирів було в автобусі спочатку?

• Чи відомо, скільки пасажирів було в автобусі спочатку? (Не відомо.) А чи відомо, на які дві частини можна поділити цих па­сажирів? (На тих, що вийшли, і тих, що залишилися.) Чи відомі обидві частини? (Так.) Покажіть їх за допомогою паличок. (Учні викладають окремо 4 і 3 палички і пояснюють, що кожна множи­на означає.) Покажіть тепер на цих паличках, де ті пасажири, які були в автобусі спочатку. (Діти об’єднують множини в одну.) То спочатку було пасажирів більше чи менше? (Більше.) Отже, якою дією розв’яжеться задача? (Дією додавання.)

Коли цю чи подібну задачу опрацьовують на третьому сту­пені, то доцільно використати короткий запис:

Було - ?

Вийшли - 4

Залишилося - 3.

Якщо потрібне обґрунтування вибору дії, то воно може бути таким:

— З яких двох частин складаються всі пасажири, які були спочатку в автобусі? (З тих, що вийшли, і з тих, що залишили­ся.) Чи відомі нам обидві частини? (Так.) Як знайти ціле, коли відомі його частини? (Треба об’єднати частини.) Якою дією розв’язується задача? (Дією додавання.)

Задача на знаходження від'ємника

У гаражі стояло 10 машин. Коли кілька машин від’їхало, в гара­жі залишилося 7машин. Скільки машин від’їхало?

Короткий запис може бути такий:

Було -10

Від’їхало - ?

Залишилося - 7

Як і в роботі з двома попередніми задачами, на ступені ознайом­лення з новим видом для правильного вибору дії буває недостатньо короткого запису. Потрібне виконання операції над множинами.

— Покладіть стільки паличок, скільки спочатку було машин в гаражі. (Діти викладають 10 паличок.) З яких двох частин скла­даються ці машини? (З тих, що від’їхали, і з тих, що залишили­ся.) Яка з цих частин відома, а яка - невідома? (Відомо, скільки машин залишилося, а невідомо, скільки від’їхало.) Покажіть на паличках, скільки машин залишилося. (Якщо діти з 10 паличок заберуть 7, отже, вони правильно уявляють ціле і його частини.) Що означають палички, які залишилися нерухомими? (Це ті ма­шини, які від’їхали.) Як ми знайшли невідому частину? (Ми від цілого забрали відому частину.) Отже, якою дією розв’яжеться задача? (Дією віднімання.)

Під час роботи над подібною задачею на третьому ступені палички вже не використовують, а якщо є потреба в обґрунтуван­ні вибору дії, то воно зводиться до з’ясування, як знайти невідому частину, коли є ціле і відома його частина.

Необхідно зазначити, що робота над простими задачами вже потребує диференційованого підходу. Адже у кожному класі є сильні, середні і слабкі учні. Якщо слабкі учні не можуть швидко опанувати цей вид задач, вони повинні мати змогу користуватися роздатковим матеріалом стільки, скільки потрібно, щоб запрацю­вала їхня уява. Якщо сильні учні можуть відразу розв’язав дачу, то їм не потрібно щоразу брати участь у її розборі. Обґрунтування вибору дії треба проводити лише з тими учнями, цього потребують. Диференційована робота над задачею бути проведена у такий спосіб.

Усі учні беруть участь в ознайомленні зі змістом задачі. І складання короткого запису на дошці (якщо це потрібно) вчитель пропонує тим учням, котрі готові розв’язувати задачу, працювати самостійно. З рештою учнів він робить обґрунтування вибору причому стежить, щоб сильніші учні, які самостійно запис розв’язання, участі в бесіді не брали. Тоді середні та слабкі повинні самі думати і відповідати на запитання вчителя, і дію обґрунтовано, більшість дітей самостійно записує розв’язання і відповідь. Ті, хто почав-працювати раніше, на цей момент закінчили роботу

і одержують додаткове завдання, наприклад змінити числові дані задачі так, щоб отримати більшу відповідь розв’язати нову задачу.

Якщо у класі є учні, котрі потребують додаткової допомоги у роботі над цієї задачею, вчитель має час з ними попрацювати коли більшість класу працює самостійно. Якщо потрібно, можна зі слабшими учнями розглянути задачу з використанням лічильного матеріалу. Коли робота завершена, один із середніх у повідомляє відповідь. За додаткове завдання сильніші учні отримують окрему оцінку під час перевірки зошитів.

За такою схемою диференційовану роботу доцільно проводити в майбутньому і над складеними задачами.