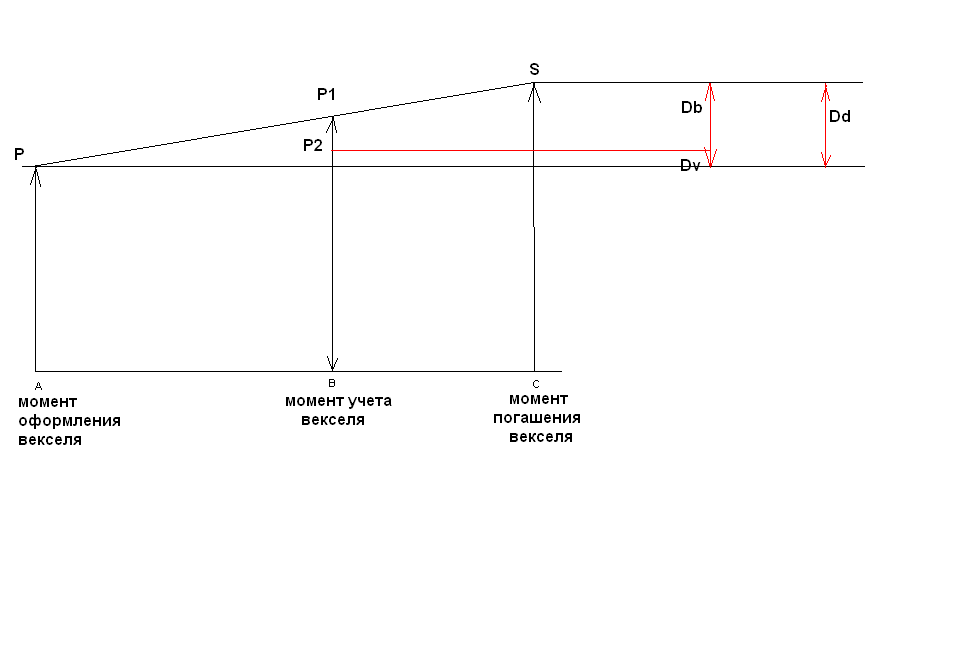
37. Логика факторного разложения дохода банка при учете векселя.

P1-теоретич.стоимость векселя в момент учета (продажи банку)

P2-предлагаема банком сумма в обмен на вексель

Db-доход банка от операции (учета векселей)

Dv-доход векселедержателя

P=S

38.Сложные проценты и их формула.

-применяются в долгосрочных фин.кредитных операциях.

-Если % не выплачиваются периодически сразу после их начисления за прошедш. Интервал времени, а присоединяются к сумме долга. Присоединение начисл. % к сумме, которая служила бы базой для их определения, часто наз. Капитализацией %.

Формула наращения по сложным %:

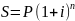
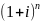- множитель наращения слож.%

В практич.расчетах в основном применяются дисконтные %-ты.

39.Эффективная и номинальная процентная ставки и ее формула.

При каждом начислении % капитализируются т.е. добавляется к сумме с начисленными в пред.периоде процентами.каждый раз % начисляются по ставке j/m.ставка j наз номинальной

Начисление по ном ставке по фор-ле:

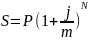
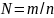- число периодов начисления

Эффективная ставка – показ., какая годовая ставка сложных % дает тот же финн результат, что и m- разовая наращения в год.j/m.если % капит-ся m раз в год, каждый раз со ставкой j/m, то можно записать след. равенство для соответствующих множителей наращения:

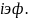-эффективная ставка

- номинал.ставка

Взаимосвязь между эфф. и ном ставкой выр-ся:

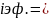
Обратная зависимость:

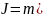
40.Дисконтирование и учет по сложным ставкам процентов и ее формула.

Мат.учет- в этом случае решается задача, обратная наращению по сложным %.

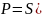
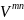• – дисконтный множитель

Также как в случае начисления простых %, Р, полученного дисконт.-ем S, наз современной или текущей стоимостью(приведенная величина S).Суммы S,P эквивалентны в том смысле, что платеж в сумме S через N лет равноценен сумме Р, выплачиваемой в настоящий момент.

Банк.учет- в этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке:

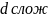- слож.годовая учетная ставка

При использ.сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, т.к. учетная ставка каждый раз применяется к сумме уменьшенной за пред.период на величину дисконта.

41.Взаимосвязь простых и сложных процентов.

Простые % используются в практике банковских расчетов при начислении % по краткосрочным ссудам сроком до 1 года.

Сложные % по инвестиц.проектам сроком более 2 лет

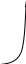
S

Cлож

простые

n

43.Постоянная рента – когда платежи равны между собой

44.Переменная рента – когда платежи НЕ равны между собой

45.Обычная рента – рента постнумерандо – все платежи осуществляются в конце интервалов времени

46.Приведенная рента – рента пренумерандо – когда все платежи осуществляются в начале интервалов ренты

47.Верные ренты – выплата не ограничена никакими условиями. Верные ренты подлежат безусловной выплате, например, при погашении кредита. 

48.Условные ренты – выплата обусловлена наступлением какого-то события, н-р, страховые взносы. Срок реализации отложенных рент откладывается на некоторое время.

49. Отложенная рента – это рента, при которой устанавливается льготный период после подписания контракта, в течение которого она не выплачивается. То есть срок реализации ренты откладывается на некоторый срок.

50. Простая рента – это величина рентных платежей, при которой число рентных платежей в году = частоте начисления процентов в году или р=m

51. Общая рента – та рента, в которой число рентных платежей в году р не равно частоте начисления процентов в году m .

52. Наращенная сумма для простой ренты постнумерандо и ее формула. Пусть R – ежегодные платежи, на которые начисляются % в конце каждого года по сложной проц.ставке i со сроком ренты n. Наращенная сумма равна:

S=R