3.2. Оптико-геометрические характеристики

В расчетах теплообмена излучением большой интерес представляет определение плотностей потоков излучения, которые возникают в системах тел разных размеров и форм, произвольно взаимно ориентированных. По-добного рода расчеты могут быть выполнены с использованием такой важ-ной оптико-геометрической характеристики, как угловой коэффициент. Фи-зический смысл этого понятия устанавливается из анализа теплообмена в системе двух серых выпуклых тел с поверхностями и и температу-рами и , расположенных в пространстве так, что одно из них «видит» другое (рис.3.4). Предполагается, что излучающее тело обладает изотропным

излучением и отражением, а разделяющая среда лучепрозрачна.

Выделенный элемент поверхности излучает по всем направлениям поток эффективного излучения = , из которого в соответствии с законом Ламберта на элемент попадает только часть

= . (3.9)

Напомним, что , а телесный угол по определению

= , (3.10)

Рис.3.3. Степени черноты СО₂ (а), СО (б), SO₂ (в), H₂O (г) и поправочный

коэффициент для расчета степени черноты

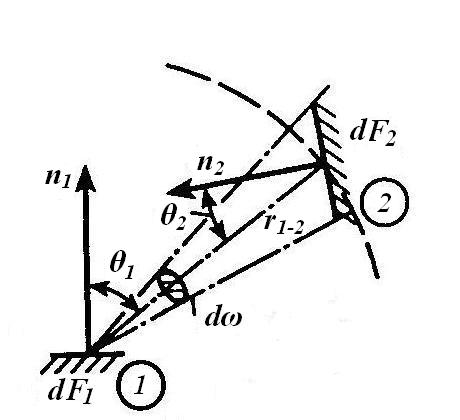
Рис.3.4. Схема к расчету теплообмена излучением между двумя телами,

произвольно расположенными в пространстве

где - расстояние между рассматриваемыми элементами. С учетом этих сведений

. (3.10 а)

Величина получила название элемен-тарного коэффициента излучения. Он равен отношению потока излучения элементарной площадки , падающего на элементарную площадку , к потоку полусферического эффективного излучения элементарной площад-ки .

Если поток излучения с на конечную поверхность отнести к потоку полусферического эффективного излучения элементарной площадки , то полученное отношение будет локальным угловым коэффициентом излучения:

. (3.11)

Средний угловой коэффициент излучения, или средний коэффициент облученности равен отношению потока излучения всей поверхности , падающего на поверхность конечного размера , к потоку полусфе-рического эффективного излучения поверхности или

(3.12)

Таким же образом может быть найден средний угловой коэффициент излучения

(3.13)

Отсюда следует, что

или ,

так как величина двойного интеграла не зависит от порядка интегрирования. Величина Н, равная произведению площади поверхности на средний угловой коэффициент излучения этой поверхности на другую, получила название вза-имной поверхности пары тел.

Заметим, что при вогнутой поверхности часть излучаемого ею потока попадает на нее же. В соответствии с этим введено понятие углового коэф-фициента излучения (элементарного, локального, среднего) поверхности на самое себя , представляющего отношение доли тепловой энергии, попа-дающей на данную поверхность, от всего излучения той же поверхности.

Приведенные оптико-геометрические характеристики обладают рядом свойств. Важнейшие из них следующие:

свойство взаимности

, (3.14)

следует из постоянства взаимной поверхности пары тел . Физии-ческая сущность этого свойства заключается в том, что при равенстве тем-ператур и коэффициентов излучения, например, двух поверхностей, поток излучения, попадающий с первой поверхности на вторую, равен потоку из-лучения, попадающему со второй поверхности на первую;

свойство замкнутости

, (3.15)

т.е. сумма угловых коэффициентов излучения с -ой поверхности на все окружающие ее поверхности и на самое себя равна единице. Это свойство следует из того факта, что поток излучения с поверхности распределяется по поверхностям, а также частично попадает и на самое себя. Иногда это свойство записывается в форме:

(3.15 а)

свойство аддитивности

(3.16)

заключается в том, что угловой коэффициент излучения с поверхности на сложную поверхность, состоящую из отдельных частей равен сумме угловых коэффициентов с -ой поверхности на каждую - ую;.

свойство невогнутости

, (3.17)

указывает на то, что плоское или выгнутое тело не может излучать само на себя.

Выше было рассмотрено излучение тела с поверхностью непо-средственно на поверхность . Однако если они окружены другими серыми телами, то энергия, излучаемая поверхностью , многократно отразится от других серых поверхностей, в том числе от и от самой себя. Отношение потока с , падающего с учетом многократных переотражений в системе на , к потоку полусферического собственного излучения поверхности характеризует разрешающий угловой коэффициент излучения .Численно он зависит от угловых коэффициентов излучения и от отражательной способности участвующих в теплообмене тел и определяется по формуле:

. (3.18)

В зависимости от способа определения различают элементарный, локальный и средний разрешающий угловые коэффициенты излучения.

Потоки излучения в системе нескольких тел могут существенно ме-няться, если внутри системы находится поглощающая излучающая среда, способная влиять на плотности потоков излучения, достигающих той или иной поверхности. В простейшем случае системы из двух поверхностей (см.рис.3.4) в отличие от предыдущего примем, что между телами находится ослабляющая среда с коэффициентом ослабления (поглощения) , одина-ковым для всего объема системы. В остальном условия теплообмена излу-чением в этой системе сохраняются прежними. Наличие ослабляющей (поглощающей) среды приводит к тому, что при движении потока излучения его поверхностная плотность будет в соответствии с законом Бугера-Бера уменьшаться пропорционально поверхностной плотности потока излучения

, коэффициенту ослабления и длине пути луча . Применительно к рассматриваемой задаче это изменение составит

. (3.19)

Обращаясь к рис. 3.4 и повторяя анализ предыдущего примера с уче-том потерь излучения за счет поглощения его средой, определим величину потока излучения, покидающего поверхность элементарной площадки , ослабленного на пути от к и попавшего на элементарную площад-ку :

(3.20)

Это выражение отличается от аналогичного (3.9) множителем , с помощью которого и оценивается развитие поглощения излучения на пути от к . Раскрывая, как и ранее , , после преобразований получим:

(3.21)

откуда следует

( )/( ) . (3.22)

Полученная оптико-геометрическая характеристика назы-вается элементарным обобщенным угловым коэффициентом излучения, ко-торый числено равен отношению потока излучения элементарной площадки, достигающего с учетом ослабления излучения средой другой элементарной площадки, к потоку полусферического излучения первой площадки. После-довательным интегрированием по , а затем по получим соответственно локальные и средние обобщенные угловые коэффициенты излучения . Для этих коэффициентов остаются справедливыми и записанные выше свойства угловых коэффициентов - взаимность, замкнутость, аддитивность и невогнутость.

Определение оптико-геометрических характерстик по приведенным выше формулам связано со значительными математическими трудностями, особенно с учетом разнообразия размеров, форм, положений в пространстве поверхностей, составляющих систему тел, в которой осуществляется теп-лообмен излучением. Позволяет их преодолеть применение современных ЭВМ. Однако наряду с расчетом угловых коэффициентов излучения в ме-таллургической теплотехнике широко используют экспериментальные ме-тоды - теплового и светового моделирования, а также инженерные методы, основанные на геометрических представлениях. Для относительно простых систем, встречающихся в практике работы металлургических печей и тепловых агрегатов, средние угловые коэффициенты можно рассчитывать с учетом их основных свойств.

Рассмотрим некоторые системы из двух тел (рис. 3.5). Для больших плоских поверхностей с небольшим расстоянием между ними (рис.3.5, а) энергия теплового излучения практически не выходит за пределы системы, следовательно, . Для двух концентрических сферических поверх-ностей или двух длинных круглых коаксиальных цилиндров (рис.3.5,б) очевидно, что всё излучение с первой поверхности попадает на вторую. Таким образом, из такого простого анализа следует = 1 и тогда на основе свойства взаимности = следует, что / , а на основе свойства замкнутости можно найти / . Аналогично определяются угловые коэффициенты и для системы (рис.3.5,в), включающей внутреннюю поверхность шарового сегмента или длинного круглого цилиндра и плоской поверхности, которые приобретают те же значения, что и в предыдущем случае. Для системы внутренних поверхностей двух полых сфер или круглых цилиндров, пересекающихся между собой (рис. 3.5, г), при определении угловых коэффициентов следует использовать гипотетическую поверхность (делитель), перекрывающую отверстие между поверх-ностями. Повторяя приведенный выше анализ, можно найти, что и и , . Если система, в которой рассматривается теплообмен излучением, состоит из трех и более тел (поверхностей), то определение для нее угловых коэффициентов осу-ществляется на основе решения соответствующих уравнений. Подобные уравнения составляют с использованием свойств угловых коэффициентов. В качестве примера такого подхода приведем определение для случая трех выпуклых тел, образующих замкнутую систему, поперечное сечение которой

дано на рис.3.5,д.

Использование свойства замкнутости дает

(3.23)

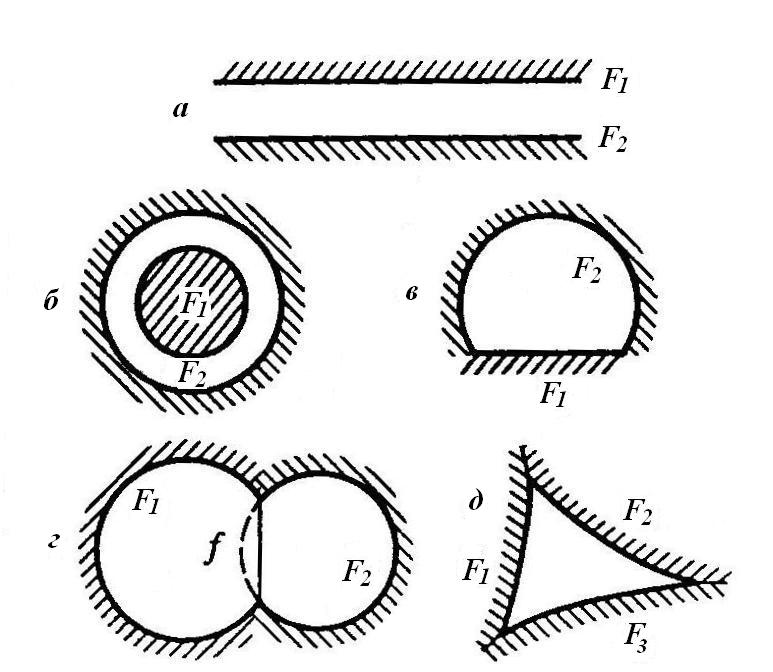
Рис.3.5. Простейшие системы излучающих тел

В этих уравнениях подлежат определению девять неизвестных угло-вых коэффициентов. Для выпуклых тел самооблучение отсутствует. Поэ-тому с учетом свойства невогнутости

. (3.24)

В результате число неизвестных сокращается до шести. Недостающие три уравнения записываются на основе свойства взаимности (3.25)

Решение систем уравнений (3.23)-(3.25) дает

(3.26)

В незамкнутой системе при определении целесообразно замкнуть ее дополнительными поверхностями так, чтобы они экранировали заданные поверхности. Такой подход, предложенный Г.Л.Поляком, позволил ему соз-дать метод «натянутых нитей», весьма удобный при отыскании угловых коэффициентов излучения для незамкнутых систем двух тел. Для случая, представленного на рис. 3.6, такими дополнительными поверхностями являются АС и ВD. Из свойства замкнутости вытекает:

. (3.27)

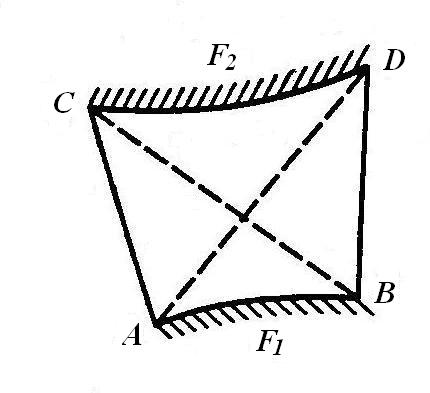
Рис. 3.6. К выводу правила «натянутых нитей»

На основании (3.26) можно записать

(3.28)

Тогда получим, что

(3.29)

или взаимная поверхность пары тел

(3.30)

откуда следует, что взаимная поверхность пары произвольно располо-женных тел равна полусумме длин внутренних нитей ( и ) минус по-лусумма длин внешних нитей ( и ). Этот вывод получил название правила «натянутых нитей». Оно применяется к поверхностям, простира-ющимся бесконечно далеко вдоль одной координаты.