2.Законы излучениея абсолютно черного тела

Законы теплового излучения получены применительно к идеальному абсолютно черному телу и термодинамическому равновесию, под которым понимают такое излучение, когда все тела, входящие в данную излу-чающую систему, принимают одинаковую температуру. Тепловое излучение представляет собой динамический процесс, при котором при одинаковых температурах каждое из тел как испускает, так и поглощает лучистую энер-гию, но в одинаковых количествах.

Значение понятия абсолютно черного тела в теории теплообмена было бы не так существенно, если бы в действительности нельзя было искус-ственно создать с высокой степенью точности модель такого тела. Моделью абсолютно черного тела может служить небольшое отверстие в стенке непрозрачного полого тела любой формы (например, сферической), если температура его всюду совершенно одинакова. Любой луч, вошедший в такое отверстие, будет поглощен практически полностью и обратно из полого тела не выйдет, хотя внутренняя поверхность стенок полости может обладать значительной отражательной способностью. Определяя такую модель как идеальный излучатель, следует отметить, что при данной температуре абсолютно черное тело излучает (поглощает) максимально возможное количество энергии.

Закон Планка. Устанавливает зависимость спектральной плотности потока излучения абсолютно черного тела от температуры Т и длины волны .

(2.1)

где - длина волны, м; = - первая константа излучения, Вт^.м²;

= - вторая константа излучениям, м^.К ; Т- температура тела, К; измеряется в Вт/м³ .

Графически эта зависимость показана на рис. 2.1. Видно, что существенно зависит от температуры и длины волны. При =0 энергия излучения равна нулю. С увеличением растет и при некотором значении достигает своего максимума, затем убывает и при становится равной нулю. С повышением температуры максимум излучения смещается в сторону более коротких волн.

Так как закон Планка получен для абсолютно черного тела, то по отношению к нечерным телам он выражает максимально возможную плот-ность потока излучения. Для нечерных тел спектральный состав излучения, кроме длины волны, зависит от физических свойств и определяется экспе-риментально.

Рис. 2.1. Спектральная плотность интенсивности излучения

Закон смещения Вина. Положения максимумов спектральной плотности излучения (рис.2.1) можно получить из экстремального значения функции по уравнению (2.1). Для этого находится производная функция по длине волны. Приравнивая производную нулю, получаем, что

, (2.2)

где - длина волны, соответствующая максимальной плотности излучения. Зависимость (2.2) выражает закон смещения Вина. Согласно этому закону максимальная величина спектральной плотности излучения с повышением температуры смещается в сторону более коротких волн.

Величина максимальной плотности излучения черного тела может быть найдена из закона Планка по уравнению (2.1), если вместо = ввести величину согласно зависимости (2.2):

, (2.3)

где - постоянная, Вт/ (м³К⁵ ). Согласно этому выражению макси-мальная плотность теплового оттока, передаваемого излучением с поверхности абсолютно черного тела, сильно зависит от температуры.

Воспользуемся этим законом для определения температуры повер-хности Солнца. В солнечном спектре величина максимальной плотности излучения приходится на длину волны м. Следовательно, температура излучающей солнечной поверхности составляет прибли-зительно К.

Закон Стефана-Больцмана. Закон был установлен опытным путем Стефаном (1879г.) и обоснован теоретически Больцманом (1881 г.). Законы Планка, Вина хорошо вскрывают особенности теплового излучения, но для инженерных расчетов их трудно использовать. Поэтому в анализе тепло-обмена излучением широко применяют интегральную плотность интен-сивности полусферического излучения . Она определяется интегрированием уравнения закона Планка по длине волны в пределах от 0 до ∞. Действительно, для абсолютно черного тела согласно определению (1.6)

(2.4)

В результате интегрирования получаем

, (2.5)

где Вт/(м²К⁴)- константа излучения абсолютно черного тела.

Уравнение (2.5) носит название закона Стефана-Больцмана. В технических расчетах этот закон применяется в более удобной форме:

(2.6)

где Вт/(м²К⁴) – коэффициент излучения абсолютно черного тела.

Следовательно, плотность потока излучения абсолютно черного тела пропорциональна абсолютной температуре в четвертой степени. Строго закон Стефана – Больцмана справедлив только для абсолютно черного тела. Однако опытами Стефана и других исследователей было показано, что этот закон может быть применен и к реальным серым телам. В этом случае он принимает вид:

(2.7)

где - степень черноты поверхности тела; c – коэффициент излучения серого тела, причем .

Величины коэффициента излучения различных тел можно найти в книгах по теплопередаче или теплотехнике.

Например, для неокисленных железа и стали коэффициент излучения равен Вт/(м²К⁴). При окислении их поверхностей коэффициент излучения увеличивается до 3,5-4,5 Вт/(м²К⁴), т.е. возрастает более чем в 10 раз. Степень черноты диалектриков (например, огнеупоров) обычно умень-шается с повышением температуры. Так, при повышении температуры с 1000 до 1550^оС степень черноты огнеупоров понижается на 20-25%. На степень черноты огнеупоров влияет шероховатость поверхности изделия. Ошлакование поверхности огнеупорного кирпича сопровождается сниже-нием его степени черноты.

Закон косинусов Ламберта. К числу основных законов теплового излучения относится также и закон Ламберта, который отражает распре-деление потоков излучения по всем направлениям, каждое из которых образует с нормалью к излучающей поверхности угол . Согласно этому закону поток излучения с элемента поверхности в направлении элемента (рис.2.2) пропорционален поверхностной плотности потока, получаемого по нормали, , умноженной на величину телесного угла и :

. (2.8)

Из анализа этого выражения следует, что наибольшее количество энергии излучается поверхностью в направлении нормали при . Для

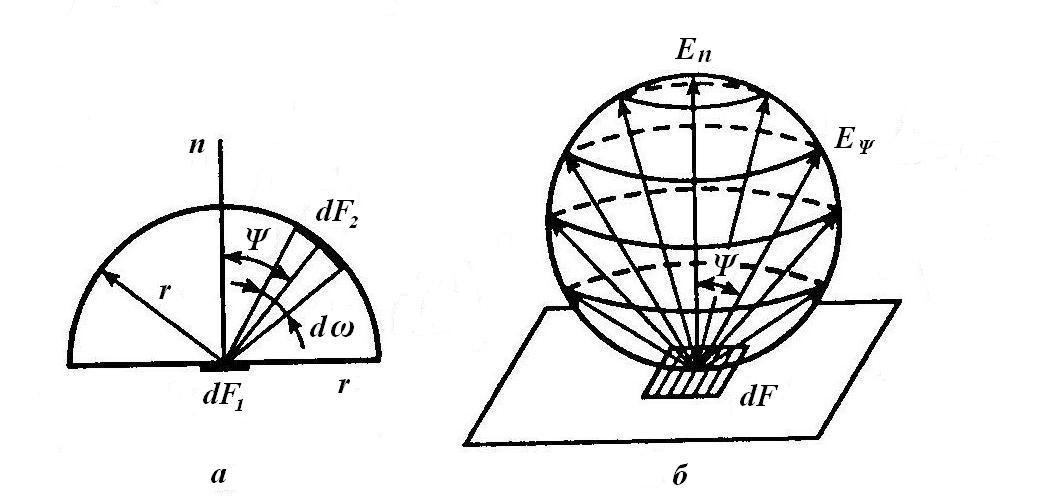
Рис. 2.2. К выводу закона Ламберта:

а – поток излучения в пределах телесного угла; б – векторы поверхностных плотностей потоков излучения

определения необходимо это уравнение проинтегрировать по повер-хности полусферы радиуса , лежащей над излучателем, и полученное вы-ражение сопоставить с формулой закона Стефана-Больцмана. Таким обра-зом, для абсолютно черного тела получим:

, (2.9)

т.е. интегральная плотность излучения в направлении нормали в раз меньше аналогичной характеристики полусферического излучения.

Из закона Ламберта вытекает важное следствие: интенсивность излучения в пределах полусферы сохраняется и не зависит от направления. Действительно, в соответствии с определением угол между выбранным направлением, к которому поверхность излучения ортогональна, и нормалью к этой поверхности всегда равен нулю. Поэтому и интенсивность излучения для любого направления будет неизменной. Такое излучение ( = const независимо от направления) получило название изотропного.

Геометрическая интерпретация закона Ламберта приведена на рис.2.2,б. Поверхностная плотность потока излучения для направления, определяемого углом к нормали излучающего элемента , представлена векторами , начинающимися на элементе и заканчивающимися на сфере, диаметр которой соответствует поверхностной плотности потока излучения в нормальном к направлении. Длины векторов соответствуют количеству энергии, передаваемой в соответствующих направлениях.

Реальные тела по своим радиационным свойствам отличаются от абсолютно черных тел прежде всего тем, что поглощают и излучают при равных температурах, площадях и ориентациях в пространстве меньше те-пловой энергии, чем идеальные излучатели.

Закон Кирхгофа. Как уже отмечалось, для оценки радиационных свойств реальных тел используют степень черноты (2.7), которая характеризует собой излучательную способность серого тела по отношению к излучению абсолютно черного тела при той же температуре и в ту же среду. Этот коэффициент изменяется в пределах от 0 до 1 и используется для характеристики интегрального и спектрального излучений.

Связь степени черноты с другими коэффициентами устанавливается на основе закона Кирхгофа. Эту связь можно получить из рассмотрения лучис-того теплообмена между двумя близко расположенными и параллельными поверхностями, разделенными лучепрозрачным газом, причем одна из них реальная, а другая – абсолютно черная. Так как расстояние между поверх-ностями относительно невелико, то излучение каждой из них обязательно попадает на другую (рис.2.3). Поверхность реального тела характеризуют температурой , плотностью потока излучения и поглощательной спо-собностью . Идеально излучающая поверхность характеризуется вели-чинами и Пусть > . Данные условия указывают на то, что абсолютно черная поверхность поглощает всю тепловую энергию, излучаемую другой поверхностью. Однако энергия поглощается реаль-ной поверхностью только в соответствии со своими свойствами, т.е. на величину . Оставшаяся часть отражается, и попав на черную поверхность, полностью ею поглощается. Таким образом, для левой повер-хности приход энергии равен , а расход - . Составив уравнение теплового баланса для реальной поверхности и разрешив его относительно результирующего потока, получим

Рис. 2.3. Система двух поверхностей, разделенных лучепрозрачным газом

. (2.10)

Тепловое излучение между поверхностями происходит и при равенстве температур = . В этом случае система находится в термодинамическом равновесии при отсутствии тепловых потерь за ее пределы и результирующий поток равен нулю ( 0). Тогда из уравнения (2.10) имеем:

= , или / = . (2.11)

Уравнение (2.11) и выражает собой закон Кирхгофа, который формулируется следующим образом: отношение излучательной способности реального тела при какой – либо температуре к поглощательной способности этого же тела постоянно и равно излучательной способности абослютно черного тела при той же температуре. Закон Кирхгофа справедлив для тел с любыми поглощательными способностями, а поэтому его можно написать в виде

. (2.12)

Следовательно, при одной и той же температуре всегда .

Подставляя уравнение выражающее закон Стефана-Больцмана применительно к реальным телам, в (2.12) получим

, (2.13)

или

, , и т.д.

Сопоставляя выражения и (2.11), получим важное следствие из закона Кирхгофа:

и т.д. (2.14)

В такой форме закон Кирхгофа показывает, что при термодина-мическом равновесии поглощательная способность и степень черноты тела числено равны между собой. Так как для реальных тел поглощательная способность всегда меньше единицы, то из соотношения (2.13) следует, что излучательная способность этих тел всегда меньше излучательной способ-ности абсолютно черного тела при той же температуре. Следовательно, при любой температуре излучение абсолютно черного тела является макси-мальным.

Из закона Кирхгофа также следует, что излучательная способность тел тем больше, чем больше их поглощательная способность. Если погло-щательная способность А тела мала, то мала и его излучательная способность Е. Поэтому тела, которые хорошо отражают лучистую энергию, сами излучают очень мало, и в частности, излучательная способность абсолютно белого тела равна нулю.

Закон Бугера-Бера. Рассмотрим несколько подробней изменение потока излучения в излучающей, поглощающей и рассеивающей средах. Пусть имеется среда, на которую падает поток энергии с интенсивностью излучения . При этом поток излучения в некотором сечении 1 будет Для оценки изменения потока излучения, обусловленного поглощением и рассеиванием энергии, используется закон Бугера, согласно которому относительное изменение интенсивности излучения при прохож-дении через элементарный слой при определенной концентрации погло-щающего вещества пропорционально длине пути луча в этом слое. В соответствии с эти законом

(2.15)

где коэффициент ослабления , м^-1 , включает коэффициенты поглощения и рассеяния :

= + .

Поток излучения может измениться и в результате собственного излу-чения объема среды, т.е.

(2.16)

где - объемная плотность собственного излучения, Вт/м³.

Указанные изменения приведут к тому, что в сечении 2 поток излучения станет равным .

Для бесконечного малого объема закон сохранения энергии запишется следующим образом:

. (2.17) С учетом того, что в пределах рассматриваемого объема значения

и могут быть приняты неизменными, последнее уравнение после преобразований примет вид:

(2.18)

Полученное уравнение характеризует изменение интенсивности излу-чения в поглощающей, излучающей и рассеивающей средах и называется уравнением переноса энергии излучения.

Если интенсивность собственного излучения среды много меньше излучения, ослабленного средой ( ), то уравнение переноса упрощается:

или (2.19)

и принимает форму закона Бугера.

Величина определяет значение падающего на поверхность слоя излучения. Энергия, поглощенная в слое толщиной , равна . В итоге поглощательную способность слоя (среды) можно представить как

/ . (2.20)

Комплекс получил название оптической толщины (плотности) слоя.

Если поток излучения ослабляется в результате изменения концен-трации вещества, то в соответствии с законом Бера относительное ослаб-ление монохроматического луча в слое заданной толщины пропорци-онально концентрации поглощающего вещества в данном слое.

Закон Бера соблюдается при малых концентрациях поглощающего вещества. С ростом концентрации возможно взаимодействие между частицами и молекулами, меняющее свойства среды, не учитываемые этим законом. Следует также отметить, что закон Бера соблюдается строго для монохроматического излучения. В противном случае коэффициенты ослабления зависят от длины волны излучения, природы поглощающего вещества и других факторов.

В расчетной практике используют объединенный закон Бугера-Бера, в соответствии с которым относительное изменение интенсивности излучения при прохождении через поглощающую среду пропорционально произведению концентрации поглощающего вещества на длину луча в поглощающей среде:

, (2.21)

откуда можно получить

. (2.22)

Закон Бугера-Бера и выводы из него справедливы для газового излу-чения запыленной среды, состоящей из абсолютно черных сферических час-тиц одинакового диаметра, подчиняющихся также законам геометрической оптики. В этом случае оптическая толщина оказывается равной , где - удельная свободная поверхность частиц. В других случаях, когда частицы имеют неправильную форму и разные размеры, при ослаблении излучения наблюдается, кроме поглощения, рассеяние и дифракция. Это приводит к необходимости учета физических свойств, геометрической структуры и размера частиц, спектрального состава падающего на частицы излучения, в замене числового коэффициента 0,25 на экспериментально, а в некоторых задачах и аналитически определяемые коэффициенты ослабления.