11. Задача использования ресурсов или задача планирования производства. Транспортная задача.

12. Задача о составлении рациона питания

13. Требуется составить ежедневный рацион питания на осно­ве имеющихся видов продуктов так, чтобы общая стоимость использован­ных продуктов была минимальной. При этом человек получает не менее определенного количества питательных веществ, например, таких, как жиры, углеводы, белки, витамины и т.п.

14. Каждый вид продуктов содержит разную комбинацию этих веществ. Из­вестна цена единицы веса каждого продукта.

15. Пусть имеются п различных продуктов P₁, Р₂, ..., Р_п и пере­чень из т необходимых питательных веществ S₁, S₂, ..., S_m. Обозначим через а_ij содержание (в весовых единицах) i -го питательного вещества в единице j -го корма, а через b i минимальную суточную потребность человека в i -м питательном веществе. Через х_j обозначим количество каж­дого вида продуктов в ежедневном рационе. Очевидно, что х _j > 0.

16. Условия задачи можно представить в виде таблицы:

17. 

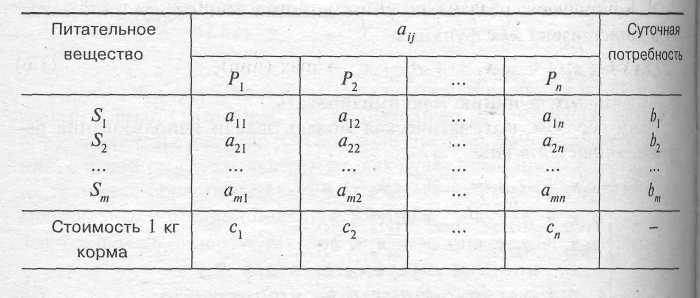
18. Для первого вида питательного вещества неравенство-ограничение примет вид: а₁₁ х₁ + а₁₂х₂ + ... + а_1пх_п> b₁

19. Аналогично запишутся неравенства и для остальных питательных веществ.

20. Общие затраты на весь рацион питания животного можно найти на основе линейной функции: Z(X) = c₁x₁ + с₂х₂ + ... + с_пх_п. Эту функцию нужно минимизировать.

21. Итак, математическая модель задачи составления рациона питания имеет вид

22. 

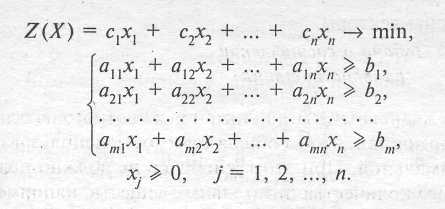
23. Геометрический метод решения ЗЛП.

1. Алгоритм геометрического метода решения задач млп

Пусть требуется найти максимальное значение функции Z(X) = с₁ х₁+ с₂х₂

при ограничениях:

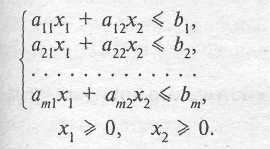
Допустим, что система ограничений совместна, т.е. имеет ре­шение, а многоугольник ее решений (ОДР) ограничен.

Каждое из неравенств определяет полуплоскость с границей

а _{i 1} х₁ + а _{i 2}х₂ = b₁ или х₁= 0, х₂ = 0. Представим этот многоугольник на плоскости Ох₁х₂ (рис. 2).

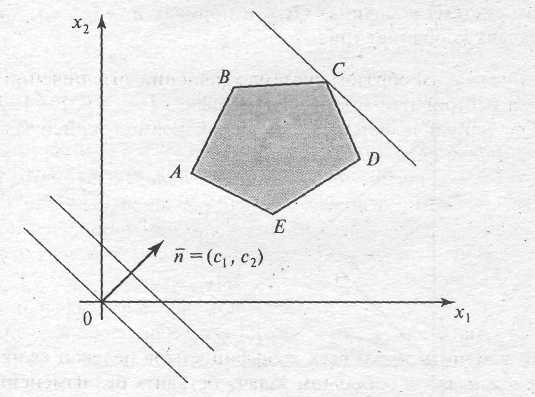
Рис 2

Линейная функция при фиксированных значениях Z(X) является уравнением прямой линии с₁х₁ + с₂х₂ = const. Изобразим прямую, соответствующую линейной функции, при Z(X) = 0. Эта прямая пройдет через начало координат. Другим значениям Z(X) будут соответствовать прямые, параллельные друг другу.

Прямая, уравнение которой получено из целевой функции задачи при равенстве ее постоянной величине, называется линией уровня.

Известно, что коэффициенты при переменных в линейном уравне­нии являются координатами нормального вектора к соответствующей прямой или плоскости. Следовательно, нормальный вектор линий уров­ня п имеет координаты с₁ и с₂, т.е. п = (с₁, с₂).

Если перемещать линию уровня параллельно ее начальному поло­жению в направлении вектора п , то для данного случая (см. рис. 2.1) последней точкой, в которой линия уровня коснется ОДР, окажется точка С.

Линия уровня, имеющая общие точки с ОДР и расположенная так, что ОДР целиком находится в одной из полуплоскостей, называется опорной прямой.

Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать параллельно начальному положению в направлении нормали, и убывают при перемещении в противоположном положении.

Таким образом, алгоритм решения задачи линейного програм­мирования с двумя переменными графическим методом таков:

1. Строится область допустимых решений.

2. Строится вектор п = (с₁, с₂) с точкой приложения в начале коор­динат.

3. Перпендикулярно вектору п проводится одна из линий уровня, например линия уровня, соответствующая уравнению с₁х₁ + с₂х₂ = 0.

4. Линия уровня перемещается до положения опорной прямой. На этой прямой и будет находиться максимум или минимум функции.