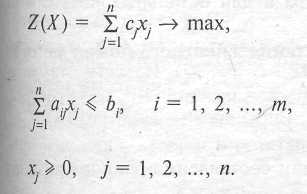3. Взаимное расположение двух прямых

Пусть на плоскости прямые l₁, l₂ заданы уравнениями общего вида:

А₁х +В₁х +С = 0

А₂х +В₂х +С = 0

Известно, что две прямые на плоскости либо пересекаются, либо параллельны, либо совпадают.

Выясним условия взаимного расположения.

1. А₁В₂ –А₂В₁ ≠ 0 или А₁/А₂ ≠ В₁/В₂,то есть нормальны векторы n₁ = (А₁, В₁) и n₂ = (А₂, В₂) данных прямых не коллинеарны, то прямые l₁ и l₂ не параллельны и не совпадают, а следовательно прямые пересекаются. Координаты точки пересечения прямых находят из решения системы уравнений.

2. А₁В₂– А₂В₁ = 0 или А₁/А₂ = В₁/В₂ (координаты пропорциональны), то есть векторы n₁ = (А₁, В₁) и n₂ = (А₂, В₂) коллинеарны, то прямые l₁,l₂ либо параллельны, либо совпадают.

Для того, что бы прямые l₁ и l₂ были параллельны необходимо и достаточно, чтобы А₁В₂–А₂В₁=0. Перепишем наше соотношение в виде -А₁/В₁ = -А₂/В₂ и умножим на -1, тогда k₁ = k₂, то есть прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны между собой.

Если прямые l₁ ┴ l₂,то векторы n₁┴n₂. Следовательно, скалярное произведение обращается в 0. Условие перпендкулярности: А₁А₂ + В₁В₂ = 0 запишем в виде является А₁/В₁ * А₂/В₂ + 1 = 0 или - А₁/В₁ * (-А₂/В₂) + 1 = 0, или -k₁*(-k₂) +1 = 0. Отсюда имеем k₁ = - 1/k_2. Таким образом, прямые взаимно перпендикулярны тогда только тогда, когда их угловые коэффициенты обратны по величине и противоположны по знаку.

10. Понятие и сущность задачи линейного программирования (ЗЛП). Моделирование задачи линейного программирования.

1. Понятие и сущность линейного программирования

Если целевая функция и система ограничений линейны, то задача математического программирования называется задачей линейного программирования.

В общем случае задача линейного программирования может быть записана в таком виде:

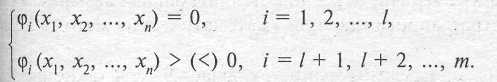
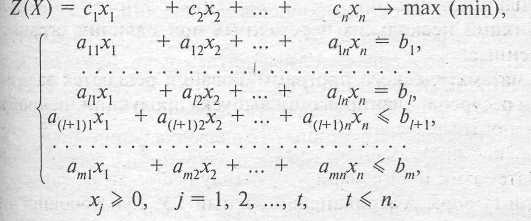
Данная запись означает следующее: найти экстремум целевой функции задачи и соответствующие ему переменные X = (х₁, х₂, .. ..., х_п). при условии, что эти переменные удовлетворяют системе ограничений и условиям неотрицательности.

Допустимым решением (планом) задачи линейного программиров ния называется любой п-мерный вектор X =(х₁, х₂, ..., х_п), удовлетворяющий системе ограничений и условиям неотрицательности.

Множество допустимых решений (планов) задачи образует область допустимых решений (ОДР).

Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение (план) задачи, при котором целевая функция достигает экстремума.

1. Моделирование задач линейного программирования.

Задача использования ресурсов

Для изготовления нескольких видов продукции P₁, P₂, ..Р_п используют т видов ресурсов S₁ ,S_2,, ..., S_m. Это могут быть различные материалы, электроэнергия, полуфабрикаты и т.п. Объем каждой вида ресурсов ограничен и известен (b₁, b₂, ..., b_т).

Известно также затраты а_ij (i = 1, 2, ..., т; j = 1, 2, ..., п)- количество каждого i -го вида ресурса, расходуемого на производство единицы j -го вида продукции. Кроме того, известна прибыль, получаемая от реализации единицы каждого продукции (с₁, с₂, ..., с_п).

Условия задачи можно представить в виде таблицы:

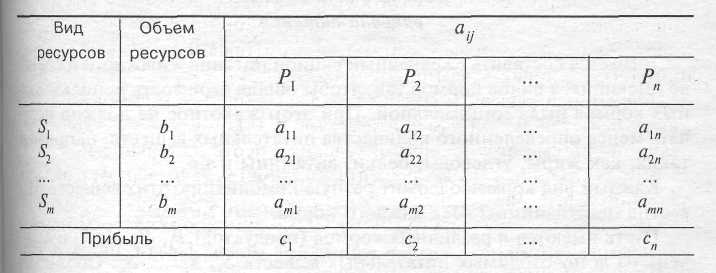
Пусть х _j (J = 1, 2, ..., п) — количество каждого вида продукции, которое необходимо произвести.

Для первого ресурса имеет место неравенство-ограничение

а₁₁х₁ + а₁₂ х₂ + ... + а₁₂ х_п < в₁

Аналогичные неравенства будут и для остальных видов ресурсов. Следует учитывать также, что все значения х _j > 0, j = 1, 2, ..., п.

Общая прибыль, получаемая от реализации всей продукции, может быть представлена как функция: Z(X) = с₁х₂ + с₂х₂ + ... + с_п х_п. Необходимо эту функцию максимизировать.

Таким образом, математическая модель задачи использования ресурсов запишется в виде

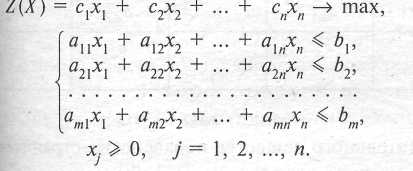
В более компактной форме целевую функцию и систему ограниче­ний можно записать, используя знак суммирования,