
- •Перечень вопросов итоговой аттестации по учебной дисциплине Элементы высшей математики для специальности 080110 Банковское дело
- •Основные свойства определенного интеграла
- •Действия с матрицами
- •Решение систем линейных уравнений методом Крамера
- •3 Решение систем линейных уравнений матричным способом
- •4 Решение системы линейных уравнений методом Гаусса
- •Понятие векторов
- •Линейные операции над векторами
- •Различные способы задания уравнения прямой
- •Взаимное расположение двух прямых
- •Понятие и сущность линейного программирования
- •Задача использования ресурсов
- •Задача о составлении рациона питания
- •Алгоритм геометрического метода решения задач млп
- •Различные случаи решения
Перечень вопросов итоговой аттестации по учебной дисциплине Элементы высшей математики для специальности 080110 Банковское дело
Предел функции. Замечательные пределы. Виды неопределенностей.
Ответ
: Число
А называется
пределом функции y
= f(x)
при
![]() ,
если для любого
,
если для любого
![]() найдется
найдется
![]() такое,
что при всех х,
удовлетворяющих
неравенству
такое,
что при всех х,
удовлетворяющих
неравенству
![]() ,
будет
выполняться неравенство
,
будет
выполняться неравенство
![]() .
Кратко это можно записать так:
.
Кратко это можно записать так:
![]()
![]()
Первый замечательный предел: Предел отношения синуса малой дуги к самой дуге, выраженной в радианах, при стремлении величины дуги к нулю равен единице:
![]()
![]()
Следствие
1-го замечательного предела:
![]() .
.
Второй
замечательный предел: Предел
последовательности
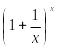 при
при![]() равен
равен
![]() :
:
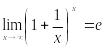 или
или
![]()
Непрерывность функции. Точки разрыва и их классификация.
Функция
y
= f(x)
называется
непрерывной в точке
![]() если для любого
найдется
такое,
что при всех х,
удовлетворяющих
неравенству
если для любого
найдется
такое,
что при всех х,
удовлетворяющих
неравенству
![]() ,
будет
выполняться неравенство
,
будет
выполняться неравенство
![]() .
.
Или
Функция
y
= f(x)
называется
непрерывной в точке
если она определена в некоторой
окрестности точки
![]() , существует предел функции при
и
он равен значению функции в этой точке:
, существует предел функции при
и
он равен значению функции в этой точке:
![]() Функция
y=f(x)
называется непрерывной на некотором
промежутке, если она непрерывна в каждой
точке этого промежутка.
Функция
y=f(x)
называется непрерывной на некотором
промежутке, если она непрерывна в каждой
точке этого промежутка.
Исходя из определений и свойств предела и непрерывности функции, можно доказать непрерывность основных элементарных функций.
Точки,
в которых нарушается непрерывность
функции, называются точками разрыва.
Точка разрыва
![]() называется
точкой разрыва первого рода, если
существуют конечные односторонние
пределы в этой точке.
называется
точкой разрыва первого рода, если
существуют конечные односторонние
пределы в этой точке.
Точка
разрыва
называется
точкой разрыва второго рода, если она
не является точкой разрыва первого
рода, т.е. хотя бы один из односторонних
пределов не существует или равен
 .
.
Производная функций одной переменной. Производная сложной функции.
Производной
функции f(x)
в
точке
называется
предел отношения приращения функции
![]() к
приращению аргумента
к
приращению аргумента![]() при
при
![]() ,
если этот предел существует, и обозначается
,
если этот предел существует, и обозначается
![]() .
Итак
.
Итак
![]()
Теорема
1: Если функция
![]() дифференцируема
в некоторой точке х,
а функция
дифференцируема
в некоторой точке х,
а функция
![]() определена
на множестве значений функции
определена
на множестве значений функции
![]() и
дифференцируема в точке
,
то сложная функция
и
дифференцируема в точке
,
то сложная функция
![]() в
данной точке х
имеет производную, которая находится
по формуле:
в
данной точке х
имеет производную, которая находится
по формуле:
![]()
Производная обратных функций (обратные тригонометрические функции). Вторая производная и производные высших порядков.
Если
функция
![]() обратима
на интервале (а, в) и имеет отличную
от нуля производную в точке х, то ее
обратная функция
обратима
на интервале (а, в) и имеет отличную
от нуля производную в точке х, то ее
обратная функция
![]() дифференцируема
в некоторой точке у:
дифференцируема
в некоторой точке у:
![]()
Дана
функция y=f(x),
дифференцируемая на
интервале (а, в), т.е.
на этом интервале
она имеет производную
![]() , являющуюся некоторой функцией от
х,
которая называется производной
первого порядка или
первой производной. Предположим, что
эта функция также дифференцируема
на интервале (а, в).
Тогда ее производная
, являющуюся некоторой функцией от
х,
которая называется производной
первого порядка или
первой производной. Предположим, что
эта функция также дифференцируема
на интервале (а, в).
Тогда ее производная
![]() называется
второй производной от исходной
функции или производной
второго порядка.
Полученная функция может вновь
оказаться дифференцируемой. Тогда ее
производная называется третьей
производной или производной
третьего порядка:
называется
второй производной от исходной
функции или производной
второго порядка.
Полученная функция может вновь
оказаться дифференцируемой. Тогда ее
производная называется третьей
производной или производной
третьего порядка:
![]() .Определение:
Производной п-го
порядка функции y=f(x),если
она существует, называется производная
от производной (n-1)-гo
порядка:
.Определение:
Производной п-го
порядка функции y=f(x),если
она существует, называется производная
от производной (n-1)-гo
порядка:
![]()
Схема исследования функции посредством производной и построение графика.
Определение. Числовая функция y=f(x) называется монотонно возрастающей (убывающей) на множестве ее области определения, если большему значению аргумента соответствует большее (меньшее) значение функции
Определить область определения функции.
Проверить является функция четной или нечетной.
Функция
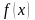 называется четной, если
называется четной, если
 для любого
для любого
 из области определения функции.
из области определения функции.
Функция
называется нечетной, если

Исследовать функцию на периодичность.
Функция
называется периодичной, если существует
такое число
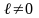 ,
что для любого
из области определения функции выполняется
равенство
,
что для любого
из области определения функции выполняется
равенство
 .
.
Исследовать функцию на непрерывность, найти точки разрыва.
Функция
непрерывна, если приращение функции
 стремится к нулю, при
стремится к нулю, при
 ,
то есть если
,
то есть если
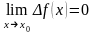 ,
то функция непрерывна.
,
то функция непрерывна.
Точки,
в которых
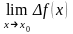 не существует или равен
,
называются точками разрыва.
не существует или равен
,
называются точками разрыва.
Найти критические точки 1 рода.
Для этого определить производную функции и приравнять ее к нулю
(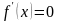 ).
Критическими называются точки, в которых
или
).
Критическими называются точки, в которых
или
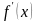 не существует.
не существует.
Найти интервалы монотонности и экстремумы функции.
Для этого методом пробных точек в каждом интервале определяют знак .
Если
 ,
то функция
на этом интервале возрастает, если
,
то функция
на этом интервале возрастает, если
 ,
то убывает.
,
то убывает.
Точка, при переходе через которую меняется знак производной , называется экстремумом.
Если меняет знак с «+» на «-» это максимум, если с «-» на «+» точка называется минимумом.
Найти критические точки 2 рода.
Для
этого определить вторую производную
 и приравнять ее к нулю
и приравнять ее к нулю
(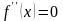 ).
).
Критическими точками называются точки, в которых или не существует.
Найти интервалы выпуклости и точки перегиба.
Для этого методом пробных точек определяют знак в каждом интервале, образованном критическими точками 2 рода.
Если
 ,
то график обращен выпуклостью вверх.
Если
,
то график обращен выпуклостью вверх.
Если
 ,
то график обращен выпуклостью вниз.
,
то график обращен выпуклостью вниз.
Точка, где меняет знак, называется точкой перегиба.
Найти асимптоты графика функции.
Прямая
 называется наклонной асимптотой. Ее
коэффициенты рассчитываются по формулам:
называется наклонной асимптотой. Ее
коэффициенты рассчитываются по формулам:
 ,
,
 .
.
Прямая
 называется вертикальной асимптотой,
если предел слева
называется вертикальной асимптотой,
если предел слева
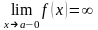 или предел справа
или предел справа
 .
.
Найти точки пересечения графика с осями координат.
Построить график функции.
Первообразная. Неопределенный интеграл, его свойства. Таблица основных формул интегрирования.
Определение: Дифференцируемая функция F(x), определенная на некотором промежутке х называется первообразной для функции f (x) определенной на том же промежутке, если для всех х из этого промежутка выполняется равенство F`(x) = f (x).
Если функция F(x) есть первообразная для функции f(x) на некотором промежутке х, то функция F(x) + C, где С- произвольная постоянная, также является первообразной для функции f (x) на том же промежутке.
Совокупность
всех первообразных для функции
f (x), определенной
на некотором промежутке х,
называется неопределенным
интегралом от функции f (x)
на этом промежутке и обозначается:

Основные свойства неопределенного интеграла
Производная от неопределенного интеграла равна подынтегральной функции
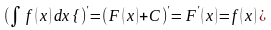
Дифференциал от неопределенного интеграла равен подынтегральному выражению

Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная

Неопределенный интеграл от алгебраической суммы нескольких функций равен сумме интегралов от них:

Постоянный
множитель можно выносить
за знак интеграла
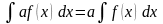
Таблица основных формул интегрирования
1.
 1а).
1а).
 2.
2.

3.
 4.
4.
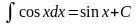
5.
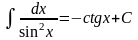 6.
6.
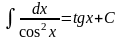
7.
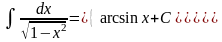 8.
8.

9.
 10.
10.

11.
 12.
12.

13.
 14.
14.

15.
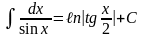 16.
16.

17.
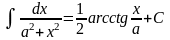 18.
18.

19.
 20.
20.

21.
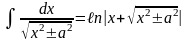
22.
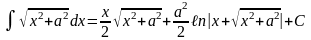
23.
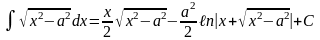
Интегрирование посредством разложения подынтегральной функции на слагаемые, посредством замены переменной, по частям.
Интегрирование в случаях, когда удается сразу воспользоваться табличными интегралами, называют непосредственным. Метод непосредственного интегрирования заключается в преобразовании подынтегральной функции и применении свойств неопределенного интеграла для приведения к табличным интегралам.
Метод подстановки заключается в том, что путем введения новой переменной удается свести заданный интеграл к новому интегралу, который берется непосредственным интегрированием.
Сделаем замену переменной интегрирования х, положив x = (t) ((t) – непрерывная функция с непрерывной производной, имеющая обратную функцию).
Тогда Метод интегрирования по частям заключается в том, что подынтегральное выражение
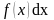 представляется в виде произведения
множителей
представляется в виде произведения
множителей
 и
и
 ,
при этом
,
при этом
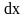 входит в
.
В результате заданный интеграл находят
по частям: сначала находят
входит в
.
В результате заданный интеграл находят
по частям: сначала находят
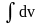 ,
а затем
,
а затем
 .
Таким образом, используется формула:
.
Таким образом, используется формула:
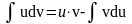
При вычислении интегралов методом интегрирования по частям главным является разбиение подынтегрального выражения на и . Существуют несколько типов интегралов:
Подынтегральное выражение содержит многочлен относительно переменной х и функции, для которых существует табличная первообразная (например cos аx; sin аx и др.), тогда за выбирают многочлен, а за все остальные множители.
Подынтегральное выражение содержит многочлен относительно переменной х и функцию, для которой не существует табличных интегралов, тогда за выбирают многочлен, умноженный на , а за принимают функцию, для которой нет табличной первообразной, но можно найти дифференциал
 .
.
В некоторых видах интегралов за функцию можно принимать любой из множителей подынтегрального выражения, если каждый из них имеет табличную первообразную.
и
 =
=
Определенный интеграл, его свойства. Формула Ньютона-Лейбница.
Определение
1: Приращение
 любой
из первообразных функций F(x)
+ C при
изменении аргумента от х=а
до х=в
функции f (x)
называется определенным интегралом и
обозначается:
любой
из первообразных функций F(x)
+ C при
изменении аргумента от х=а
до х=в
функции f (x)
называется определенным интегралом и
обозначается:

