10.3. Использование теории множеств в абстрагировании

Одно абстрактное понятие может содержать в себе множество менее абстрактных, а те в свою очередь могут состоять друг с другом в различных логических отношениях, а именно: вхождение (лексические выражается союзом «В», либо соответствующими ему по смыслу выражениями); пересечение объёмов понятий (союз «И»); сложение объёмов понятий (союз «ИЛИ»); логическая разность (союз «БЕЗ»). Изучением этих и других логических отношений занимается логика предикатов (высказываний) и математическая теория множеств. Классическую теорию множеств первым начал разрабатывать выдающийся немецкий математик конца XIX – начала XX веков Георг Кантор. Эту теорию можно использовать в историческом научном моделировании в качестве эффективного методического инструмента систематизации, формализации и алгоритмизации исторической информации.

Таким образом, понятию «абстракция» соответствует понятие «множество». Историк в этом смысле занимается выявлением и изучением множеств событий и объектов прошлого, а также отношений между этими множествами и элементами (микрособытиями), входящими в них.

Конкретизации абстрактных понятий соответствует задавание состава множества.

Задать множество можно двумя способами:

1. С помощью определения условий и признаков вхождения элементов в множество, то есть конкретных исторических фактов – в абстракцию.

2. С помощью полного или частичного перечисления состава множества. Число элементов в множестве показывает мощность множества (для историка исторический масштаб события).

Операции задавания множества особенно часто используются в методе исторической типологизации.

В историческом исследовании не всегда возможно полное перечисление состава масштабных событий и явлений. Такие трудности вызваны с одной стороны огромным объёмом информации о некоторых исторических событиях, с другой стороны – слишком недостаточной информацией о других событиях. Преодоление первого препятствия возможно с помощью создания электронных баз данных по историческому прошлому и компьютерных интеллектуальных баз знаний с автоматизацией анализа и представления информации. Именно для этих целей историк должен владеть основами математической логики.

Основные обозначения логических отношений:

 знак вхождения одного множества в другое, читается A  B – «A содержит B», «B входит в А»;

 знак принадлежности элемента к множеству, читается a A – «элемент a входит в множество А» или «множество А содержит элемент a»;

 знак пересечения объёмов множеств, читается A  B – «A пересекается B», «A и B одновременно»

 знак сложения (объединения множеств), читается A  B – «A или B» «A объединённое с B», «A вместе с B»

\ знак логической разности, читается A \ B – «A без B»

Отношение между абстрактными понятиями можно описывать на естественном литературном языке исторического повествования, на формализованном языке математической логики, а также с помощью так называемых диаграмм Венна. Английский логик конца XIX – начала XX веков Джон Венн разработал графический аппарат для визуализации отношений между объёмами понятий и множеств. Диаграммы Венна – это плоские фигуры, отношения между которыми в пространстве, а также их раскраска, соответствуют логическим отношениям между обозначаемыми этими фигурами понятиями⁵⁴.

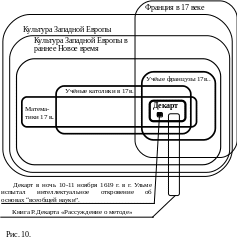
Ниже приведён пример того, как одно и то же историческое явление можно описывать на естественном языке, на формализованном языке логики, и с помощью диаграмм Венна (рис. 10).

История Франции в XVII веке связана с историей культуры Западной Европы в целом, которая в это время характеризуется специфическими чертами культуры раннего Нового времени. Одной из таких черт было становление научного мировоззрения. В ходе этого становления можно рассмотреть деятельность математиков французов католического вероисповедания, среди которых особо выделяется Рене Декарт. Одним из переломных моментов в судьбе Р.Декарта была ночь 10-11 ноября 1619 г. в г. Ульме, где он испытал интеллектуальное откровение об основах “всеобщей науки”. Один из основных трудов Р.Декарта – книга «Рассуждение о методе», которая сохранилась до наших дней и оказала значительное влияние на западную науку и философию.

Тот же текст с использованием правил логической формализации высказываний можно представить следующей форме:

(Фрация в XVII веке  (Культура Западной Европы  Культура Европы в раннее Новое время  Становление научного мировоззрения  ((Математики  Учёные католики  Учёные французы)  Декарт  Декарт в ночь 10-11 ноября 1619 г. в г. Ульме испытал интеллектуальное откровение)))  Книга Р.Декарта «Рассуждение о методе».

На рис. 10. тот же текст, выраженный с помощью диаграмм Венна. На диаграммах Венна с помощью площадей фигур можно также показать соотношение масштабов или объёмов понятий и обозначаемых ими явлений. На рис. 10. такое соотношение не учитывается, однако приблизительное соотношение объёмов понятий, соответствующее степени абстрагирования от исторической конкретики, указано с помощью толщины линий (чем тоньше линия, тем абстрактнее событие).

Отношения между понятиями, явлениями и событиями можно представить также в матрице данных, где в названиях строк и столбцов будут обозначения понятий или исторических явлений и событий, а в ячейках – обозначения логических отношений между ними.

Становление научного

мировоззрения