22 Цифрлық сигналдарды табу/демодуляциялау.

Демодуляция және айқындау(табу). Т сигналын жіберу аралығында, бинарлы қысқажолақты жүйе g1(i) және g2(i) түрінде берілген мүмкін болатын екі сигналдың біреуін жібереді. Сол сияқты бинарлы жолақты жүйе s1(0) және s2(0) түріндегі мүмкін болатын екі сигналдың біреуін жібереді. Демодуляция мен табу жалпы айтылуы ұқсас болғандықтан,таржолақты және жолақты жүйе үшін шын мәнінде S(t) записін тарату сигналын табу үшін қолдануға сәйкес келеді. Сол сияқты, әртүрлі екілік сигнал арнасын (О, Т), интервалы арқылы тарату келесі үлгіде көрсетіледі. { sl(t),0 < t < Т символы үшін, 1 [s2 (t),0 < t < Т О символы үшін. Қабылданған сигнал r(t) шудың әсер етуінен n(t) және арнаның идеалды емес импульсті сипаттамасынан hc(t) бұрмаланады.(4.12) формулада көрсетілген. r(tO = Si(t)*hc(t) + n(t) (4.12)

Біздің жағдайда n(t) AWGN орташа нольдік процесспен болжайды, ал "*" белгісі үйірткі операциясы арқылы анықталады. hc(t) функциясы бар үйірткі сигналдың сапасын бинарлық тарату идеалды, бос бұрмалану арнасы үшін нашарлатпайды, r(t) түрін ықшамдауға болады (идеальды жағдай үшін hc(t) -импульсті функция).

r{t) = si{t) + n{t) i=l,2 0<t<T (4.13)

Кейбір авторлар "демодуляция" және "табу"терминдерін синоним ретінде қолданады. Демодуляцияны (demodulation) - біз қайта өңдеу сигналы сияқты (тасушы емес таржолақты импульс), ал табуды (detection) - осы сигналдың цифрлық мәнін қабылдау шешіміне қатысты сияқты анықтаймыз.

Демодуляция/табу цифрлық сигналдарының екі негізгі кезеңі болып табылады.

Осы шарттық ықтималдық тығыздық 4,9 суретте көрсетілген.

Рисунок 4.9 – Шарттық ықтималдық тығыздық: p(z\s2) и p(z/s₁)

23 Гаусстық шуда екілік сигналдарды табу.

Демодуляция және табу бөлімінде жолақты үлгі, практикалық ұқсас таржолақты үлгі процесі анықталған. Себебі қабылданған жолақты сигнал бастапқы кезінде таржолақты содан кейін мүлдем айқындамауға түрлендіреді. Іс жүзінде Эквиваленттік теореманы келесі образбен анықтаймыз: кейінгі беттесу сигналы сызықты өңдеу сигналы арқылы орындалады. "Беттесу сигналы" жиілікті түрлендіру және араластыру процесі, араластыру спектр сигналын шақырту арқылы белгіленеді.Эквивалентті теореманы зерттей отырып сызықты үлгі өңдеу сигналынтардолақты сигналға қолдануға болады. Бұл көп цифрлық байланыс жүйесін анализдеу және сипаттау арқылы өңдеп, таржолақты тарату арнасын оқи отырып анықтайды.

24 Келістірілген сүзгі. Келістірілген сүзгі – бұл жобалау, шығысында тарату сигналын сигнал/шумен байланысу үшін жоғары мәліметтерді жібіру үшін арналған сызықты құрылғы. Уақытқа қатысты инварариантты,сызықты сүзгінің кірісіне s(t) белгілі сигналы және AWGN n(t)қосымша шуы берілсін. t= T болған кезде z(T) дискретизация құрылғысының шығысындағы сигнал aj сигналының компонентінен және По шуының компонентінен тұрады. Дисперсия шума на выходе (средняя мощность шума) записывается как ао, так что отношение мгновенной мощности шума к средней мощности шума, (S/N)T, в момент t = Т вне устройства дискретизации на этапе 1 равно следующему.Шығыстағы шудың дисперсиясы ао.

4.18

Бизге (S/N)T мәні жоғары болатын Ho(f) фильтрінің беріліс функциясын табу керек. Фильтрдың шығысындағы аj сигналын Ho(f) фильтрының беріліс функциясы және Фурьемен сипаттауға болады.

_ai(t)=]H(f)S(f)e²*^ftidf (4.19)

где S(f) — Фурье- s(t) кірістегі сигналдың кейпі. Егер қуаттың екіжақты спектрлік тығыздығы N0/2 Вт/Гц болса, шудың қуатын келесі түрде жазуга болады.

4.20

(4.18) и (4.20) формлаларын қосып, (S/N)T үшін келесіні аламыз.

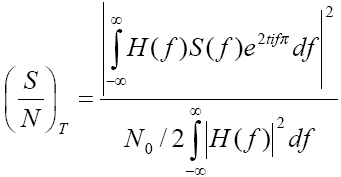4.21

25 Өту жолағымен шектелген арна арқылы цифрлық сигн/ды тарату ерекшеліктері. 4.9 суретте корсетилген(22 сұрақта) бинарлы шешім қабылдау кезінде қате пайда болуының екі мүмкіндігі бар. Ошибка е появится при передаче Егер z(t) жіберілген сигналдың деңгейі арнаның шуының әсерінен у₀-ге дейін төмендесе жіберуде е қателігі туындайды ,оның ықтималдығы келесідей.

Бұл мүмкіндік 4,9 суреттегі штрихталған облыспен көрсетілген.Осы сияқты қателік S2(t) сигналын жіберуде арна шуының әсерінен z(t) жіберілген сигналының деңгейі Yo-ден жоғары болса пайда болады.Оның ықтималдығы

қателіктің суммалық ықтималдығы барлық пайда болатын ықтималдықтар суммасына тең болады.Бинарлық кез үшін қате биттің пайда болу ықтималдығы келесідей өрнектеледі.

(4.29)-(4.31) формулаларын қосып, нәтижесінде

аламыз.

Тең априорлы ықтималдық (т.е. P(si) = P(s2) = 1/2) келесідей.

Ықтималдық тығыздығының симметриялығын қолдана отырып келесіні аламыз.

Мұнда у0 =(а1+а2)/2— оптималды шек(порог). p(z\s2) осыны гасстық эвивалентке(4,3 формуладан) ауыстыра отырып келесні аламыз

Мұнда Q(x) қатенің гаусстық итегралы. Бұл функция төмендегідей анықталады. Барлық анықтамалар гаусстық шу кезінде қателік ықтималдығын сипаттуда жарамды. Q(x) аналитикалық түрде есептеуге болмайды.Q(x) функциясының жақсы апроксимациясын жай функциялапмен де табуға болады. Төмендегі х>3 үшін келетін бір апроксимацияға мысал.