61. Боуз-Чоудхури-Хоквингэм кодтары.

. Бұл Боуз, Чодхури және Хоквинхем жасап шығарған кодтар (қысқартқанда БЧХ кодтары) қателердің кез-келген санын табуға әне жөндеуге мүмкіндік береді. Кодалау кезінде берілгендер болып жөнделуі тиіс s қателер саны және жолға (линияға) жіберілетін символдардың жалпы саны, яғни n сөздің ұзындығы табылады. k ақпараттық символдардың және m бақылау символдарының сандары, сонымен қатар бақылау символдарының құрамы анықталуы тиіс.

Кодалау әдістемесі мынадай.

1. сөздің ұзындығын таңдау. БЧХ әдісі бойынша кодалау кезінде n сөздің ұзындығын еркін таңдауға болмайды. Бірінші шектеу болып сөздегі символдар саны тақ болу керектігі табылады. Алайда тіпті бұл кезде де сөздің ұзындығын кез-келген тақ сан құрай алмайды. Бұл жерде екі жағдай болуы мүмкін: 1) берілген n бойынша теңдігін қанағаттандыратындай h санын табамыз. Мысалы, n=7 болғанда h=3, n=15 болғанда h=4, n=31 болғанда h=5, n=63 болғанда h=6 және т.б.; 2) келесі теңдеуді қанағаттандыратындай h санын табамыз

(7.25)

мұндағы h>0 – бүтін сан, ал g – n-ді оған бөлгенде n бүтін тақ сан болып шығатын тақ оң сан.

-ді көбейткіштерге жіктей отырып, келесідей n және g сандарын аламыз:

Осылай, төртінші жолдан h=6 болғанда сөздің ұзындығы тек 63-ке тең болып қана қоймай (бірінші жағдай), 21-ге де тең бола алатындығын (q=3) көреміз.

2. Кодтық арақашықтықты анықтау. Кодтық арақашықтықты 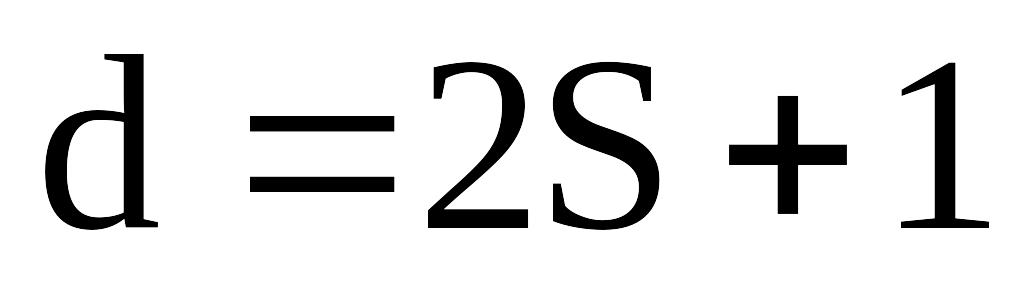-ке сәйкес анықтайды.

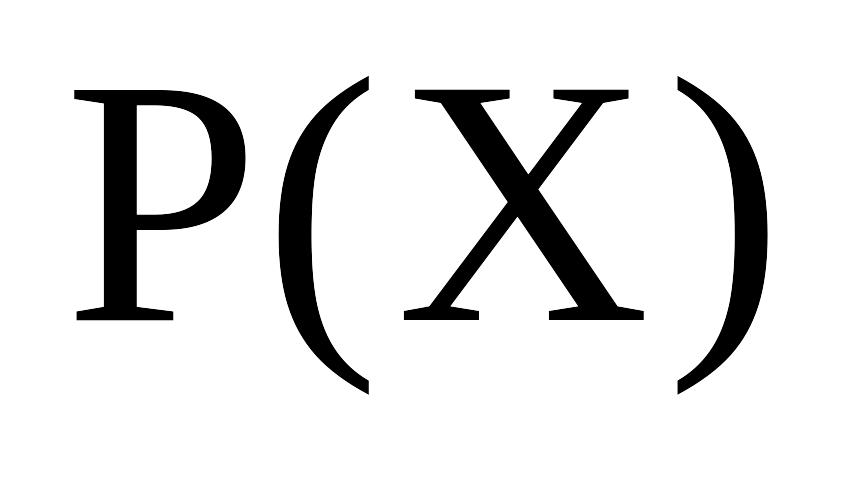3. құраушы көпмүшесін анықтау. Құраушы көпмүше дегеніміз бұл 2s-1 ретіне дейінгі (осы реттің өзін қоса) минимальді көпмүшелерінің ең кіші ортақ бөлгіші (ЕКОБ), соның ішінде құраушы көпмүше тақ минимальді көпмүшелердің белгілі бір санының көбейтілуінен құралады:

(7.26)

Минимальді көпмүшелер жай келтірілмейтін көпмүшелер болып табылады, бірқатарының анықталу әдісі [26]-да беріледі. Минимальді көпмшелердің арасында екі бірдейі бола қалған жағдайда, оның біреуі шығарып тасталатынын ескерген жөн.

2. Минимальді көпмүшелердің саны L-ді анықтау. (7.26) теңдеуінен минимальді көпмүшелердің реті 2s-1 деп анықталады деген ұйғарымға келуге болады. Егер бұл құраушы көпмүше тек тақ минимальді көпмүшелерден тұратынын ескерсек, онда олардың саны жеңіл анықталады. Мысалы, егер s=3 болса, онда 2s-1=5. Бұл (7.26) теңдеуінде , және минимальді көпмүшелері жазылады, яғни, L=3 дегенді білдіреді. Егер s=8 болса, онда 2s-1=15, және теңдеуде , , , , , , , минимальді көпмүшелері жазылады, яғни, L=8. Осылайша, минимальді көпмүшелер саны жөнделетін қателер санына тең:

L=s (7.27)

2. Минимальді көпмүшенің үлкен дәрежесі l-ді анықтау. l дәрежесі дегеніміз n-ға немесе ng-ға бүтіндей бөлінетіндей, яғни, немесе болатындай ең кіші бүтін сан. Бұдан шығатын қорытынды бұл

l=h (7.28)

2. Минимальді көпмүшелерді таңдау. Минимальді көпмүшелердің саны L мен үлкен көпмүшенің дәрежесі l анықталған соң, көпмүшелерді кестеден көшіріп жазып аламыз. Бұл кезде ЕКОБ тек l үлкен дәрежелі көпмүшелерден ғана құралмайды. Бұл, жекелей алғанда, төртінші және алтыншы дәрежелі көмүшелерге қатысты.

3. құраушы көпмүшесінің дәрежесін анықтау. Құраушы көпмүшенің дәежесі ЕКОБ-қа тәуелді болады және ls немесе lL көбейтулерінен аспайды, себебі L=s. Барлық минимальді көпмүшелерді тапқан соңқұраушы көпмұшені (7.26) теңдеуі бойынша табамыз.

4. Бақылау символдарының санын анықтау. Бақылау символдарының саны m құраушы көпмүшенің дәрежесіне тең болғандықтан, n ұзындықты кодта

(7.29)

2. Ақпараттық символдарының санын анықтау. Оны қалыпты ретпен k=n-m теңдігінен шығарады. Кодалаудың одан арғы этаптары болатын циклдік кодтар үшін қаралған этаптарға ұқсас, яғни, барлық кодтық комбинацияларды сол бойынша есептеу үшін қосымша матрицаны табамыз.

БЧХ кодтарын мұнда қысқартылған түрде берілген [26,18] кестесінің көмегімен де құрауға болады. Алдында баяндалған әдістемеге сәйкес кестеде берілген n кодтық комбинацияның ұзындығы мен s жөнделетін қателер саны бойынша k ақпараттық символдар саны мен құраушы көпмүшесі есептеп шығарылған. m бақылау символдарының саны m=n-k теңдеуінен анықталады, ал құраушы көпмүшенің ондық цифрлар түріндегі жазылуы әрбір ондық цифрды екілік кодқа аудару жолымен түрлендіріледі. Мысалы, кестенің бірінші жолында . 1 цифрына 001 екілік саны сәйкес келеді, ал 3 цифрына – 011 саны сәйкес келеді. көпмүшесі түрінде жазылатын 001011 екілік санын аламыз. Осылайша, екілік баламаға бүтіндей ондық сан емес, әрбір ондық цифр аударылады. Расында, 13 санына көпмүшесі сәйкес келеді. 3.17 кестесінен n=15, k=7 және s=2 болғанда көпмүшесіне сәйкес келетін құраушы көпмүше екендігін көреміз.

Қателерді табуға арналған БЧХ кодтары. Оларды былайша құрады. Егер қателердің жұп санын табатын код құру қажет болса, онда берілген r саны бойынша d және s мәндерін табамыз. Одан арғы кодалау осыған дейінгідей орындалады. Егер қателердің тақ санын табу қажет етілсе, онда s-тің жақынырақ орналасқан ең кіші бүтін санын тауып, кодалау осының адындағы жағдайдағыдай орындалады, тек бір ғана өзгешелігі, (7.26)-ға сәйкес табылған құраушы көпмүше қосымша екімүшесіне көбейтіледі. Мысалы, n=15 болғанда жеті қате табатын код құру қажет делік. d=8, ал s-тің жақынырақ орналасқан ең кіші мәні s=3 екендігін табамыз. Әрі қарай 3.5 мысалда келтірілгендей, көпмүшесін анықтап, оны екімүшесіне көбейтеміз, яғни, аламыз. Осылайша БЧХ(15,4) коды құралды.

62. Файрдың циклдік коды. Қателер дестесін табатын және жөндейтін циклдік кодтар (Файр кодтары). Ұзындығы b қателер дестесі деп кедергілермен зақымдалған шеткі разрядтарының арасында b-2 разряды бар кедергі комбинацияларының түрін айтады. Мысалы, b=5 болғанда кедергі комбинациялары, яғни, қателер дестесі келесідей түрде болуы мүмкін: 10001 (тек екі шеткі символ ғана зақымдалған), 11111 (барлық символдар зақымдалған), 10111, 11101, 11011 (тек бір ғана символ зақымдалмаған), 10011, 11001, 10101 (үш символ зақымдалған). Қай нұсқасында да берілген ұзындықтағы дестенің шеткі символдарының зақымдануы міндетті шарт болып келеді.

Файр кодтары ұзындығы қателер дестесін жөндей алады және ұзындығы қателер дестесін таба алады [Файр кодтарындағы кодтық арақашықтық түсінігі d екендігін қаперге аламыз].

Файр кодының құраушы көпмүшесі мына өрнектен анықталады:

(7.19)

мұндағы – l дәрежелі келтірілмейтін көпмүше.

Код құру принципіне сүйенсек, онда

(7.20)

(7.21)

Мұнымен қатар, c саны e санына бүтіндей бөлінбеуі тиіс, мұндағы

(7.22)

P(X) келтірілмейтін көпмүшесін (7.20) теңдеуіне сәйкес, бірақ (7.22) шарты қанағаттанатындай етіп кестелерден таңдап алынады. Сөздің n ұзындығы c және e сандарының ең кіші ортақ бөлгішіне тең, себебі тек осы жағдайда ғана көпмүшесі -ға қалдықсыз бөлінеді [ болғанда ешқандай көпмүшесі -ға бөлінбейді]:

n=ЕКОБ(е,c) (7.23)

Бақылау символдарының саны

(7.24)

Дестеге топталмаған, яғни, сөздің ұзынынан шашыраған қателерді жөндеу кезіндегі ұзындығы қателер санымен бірдей кодтың артылуын салыстыру көңіл аудартады. Егер бұл мақсат үшін БЧХ кодтарын және n=127 жақын мәнін пайдалансақ, онда s=4 болған кезде баяндалған әдістеме бойынша бақылау символдарының саны m=28, яғни (127, 99) коды алынғандығын есептеп шығаруға болады. Мұндай кодтың артылуы И=28/127=0.22, яғни Файр кодына қарағанда едәуір жоғары. Бұл көрініп-ақ тұр: бір жерде орналасқан төрт қатені жөндеу комбинацияның ұзынынан шашыраған қателерді жөндеуден оңайырақ.

Келесідей ереже барын есте ұстайық: егер циклдік код тәуелсіз қателерді табуға есептелген болса, ол сонымен қатар ұзындығы m қателер дестесін де таба алады.

63. Рид-Соломон кодтары. Үйірткілі кодтар

Рид-Соломон кодтары (Reed-Solomon code, R-S code) – бұл символдары m-биттік тізбектер болып келетін екілік емес циклдік кодтар, мұндағы m – 2-ден үлкен оң бүтін сан. (n,к) коды n мен k-ның барлық мәндерінде m-биттік символдарда анықталған, олар үшін

(7.30)

мұндағы k – кодалануы тиіс ақпараттық биттер саны, ал n – кодаланатын блоктағы кодтық символдар саны. Көпшілік үйірткілі Рид-Соломон кодтары үшін (n, к)

(7.31)

мұндағы t – символдағы код түзей алатын қате биттер саны, ал n-k=2t – бақылау символдарының саны. Кеңейтілген Рид-Соломон кодын n=2^m немесе n=2^m+1 болғанда алуға болады, бірақ бұдан артық болмауы керек.

Рид-Соломон коды ұзындығы кодердің кіріс және шығыс блоктарының ұзындығымен бірдей сызықтық код үшін мүмкіндігінше минимальді арақашықтықтың ең үлкеніне ие. Екілік емес кодтар үшін екі кодтық сөз арасындағы арақашықтық (Хэммингтің арақашықтығына ұқсас) символдар саны ретінде анықталады, тізбектер осылармен өзгешеленеді. Рид-Соломон кодтары үшін минимальді арақашықтық былайша анықталады.

(7.32)

t-да немесе биттің аз санындақатесі бар бұрмаланған символдардың барлығын жөндейтін кодты былайша өрнектеуге болады.

(7.33)

Мұндағы │x│ х-тен аспайтын ең үлкен бүтін санды білдіреді. t символдық қателерді жөндейтін Рид-Соломон кодтары 2t-дан артық бақылау символдарын қажет етпейтіні (7.34) теңдеуінен көрініп тұр. (7.34) теңдеуіне қарап, декодердің жөнделетін қателер санынан екі есе асатын n-к “қолданылатын” артық символдары бар деп түйіндеуге болады. Әрбір қате үшін бір артық символ қатені табу үшін және біреуі – дұрыс мәнін анықтау үшін қолданылады. Кодтың өшірулерді түзету қабілеті былайша өрнектеледі.

(7.34)

Қателер мен өшірулерді бір мезгілде түзету мүмкіндігін талап ретінде өрнектеуге болады.

(7.34)

Мұндағы α – жөндеуге болатын символдық қате комбинациялар саны, ал γ – жөнделуі мүмкін символдық өшірулер комбинацияларының саны. Рид-Соломон кодтары тәрізді екілік емес кодтардың артықшылықтарын келесі салыстыруда көруге болады. (n,к)=(7,3) екілік кодын қарастырайық. n-кортеждердің толық кеңістігінде 2ⁿ=2⁷=128 n-кортеж бар, оның ішіндегі 2^k=2³=8 (немесе барлық n-кортеждердің 1/16 бөлігі) кодтық сөздер болып табылады. Енді әрбір символы m=3 биттен тұратын (n,k)=(7,3) екілік емес кодын қарастырайық. n-кортеждер кеңісігінде 2^nm=2²¹=2 097 152 n-кортеж бар, оның ішінде 2^km=2⁹=512 (немесе барлық n-кортеждердің 1/4096 бөлігі) кодтық сөздер болып табылады. Егер амалдар әрбіреуі m-биттермен құрылған екілік емес символдармен жүргізілетін болса, онда мүмкін болатын n-кортеждердің тек болмашы бөлігі ғана (яғни, үлкен 2^nm санының ішінен 2^km) кодтық сөздер болып табылады. Бұл бөлік m өскен сайын кеми береді. Бұл жерде кодтық сөздер ретінде n-кортеждер кеңістігінің болмашы бөлігі қолданылса, d_min-ның үлкен мәніне қол жеткізуге болатындығы маңызды болып табылады.

Егер барлық n-к өшірілген символдары бақылау символдарына келетін болса, кез-келген сызықтық код символдық өшірулердің n-к комбинацияларын жөндеуге мүмкіндік береді. Алайда Рид-Соломон кодтарының блоктағы өшірулердің n-к символдарының кез-келген жиынтығын жөндей алатын тамаша қасиеті бар. Кез-келген артылулы кодтар құрастыруға болады. Дегенмен, артылу үлкейген сайын оны жоғарыжылдамдықты жүзеге асыру күрделілігі де өседі. Сол себепті ең қызықтыратын Рид-Соломон кодтары кодалаудың жоғары дәрежесіне (төмен артылуға) ие.

Үйірткілі кодтар. Сызықтық блоктық кодтың екі бүтін сан n және k-мен және полиномды немесе матрицалық генератормен сипаталатын ерекшелігі бұл кодтық сөздердің n-кортеждерінің әрқайсысы кіріс хабардың k-кортeжімен анықталатындығы болып табылады. k бүтін саны блоктық кодердің кірісін құратын мәліметтер битінің санына көрсетеді. n бүтін саны – бұл кодердің шығысындағы сәйкес кодтық сөздегі разрядтардың жиынтық саны. Кодтың кодалау дәрежесі (code rate) деп аталатын k/n қатынасы қосылған артылудың шамасы болып табылады. Үйірткілі код n, k и K үш бүтін санымен сипатталады, мұндағы k/n қатынасының кодалау дәрежесінің мәні (кодаланған битке келетін ақпарат) блоктық кодтағыдай болады; алайда n блоктық кодтағы тәрізді блоктың немесе кодтық сөздің ұзындығын анықтамайды. K бүтін саны кодтық шектеу ұзындығы (constrain! length) деп аталатын пареметр болып табылады; ол кодалаушы ығыстыру регистріндегі k-кортеждің разрядтарының санын көрсетеді. Үйірткілі кодтардың блоктық кодтармен салыстырғандағы маңызды ерекшелігі кодерде жады болатындағында – үйірткілі кодалау кезінде алынатын n-кортеждер тек бір кіріс k-кортежінің ғана емес, осының алдындағы К-1 кіріс k-кортеждерінің де функциясы болып табылады. Тәжірибе кезінде n мен к - бұл шағын бүтін сандар, ал K кодтың қуаты мен күрделілігін бақылау мақсатында өзгеріп отырады

7.4 сурет – Байланыс арнасындағы кодалау/декодалау және модуляция/демодуляция

64. Түзетуші кодтарды декодалау әдістері. Циклдік кодтарды декодалаудың бірнеше тәсілдері бар. Солардың бірі келесідегілерден тұрады:

1. Қалдықты (синдромды) есептеу. Қабылданған комбинацияны Р(Х) құраушы көпмүшесіне бөледі. R(X)=0 қалдығы комбинациялар қатесіз қабылданғанын білдіреді;

2. Қалдық салмағы W-ді есептеу. Егер қалдық салмағы жөнделетін қателер санына тең немесе одан аз, яғни W≤s болса, онда қабылданған комбинацияны модуль 2 бойынша қалдықпен қосып, жөнделген комбинацияны алады;

3. Бір символға солға қарай циклдік ығысу. Егер W>s болса, онда солға қарай циклдік ығысу жасап, алынған комбинацияны тағы да құраушы көпмүшеге бөледі. Егер қалдық салмағы W≤s болса, онда циклдік ығыстырылған комбинацияны қалдықпен қосып, содан соң оны кері бір символға оңға қарай циклдік ығыстырады. Нәтижесінде жөнделген комбинация алынады;

4. Қосымша солға қарай циклдік ығысу. Егер бір символға циклдік ығысудан кейін де бұрынғыдай W>s болса, онда қосымша солға қарай циклдік ығысулар жасайды. Бұған қоса әрбір ығысқан сайын ығыстырылған комбинацияны Р(Х)-ке бөліп, қалдық салмағын тексереді. W≤s болғанда 3п.-те көрсетілгендей әрекетттер орындалады, тек бір ғана өзгешелігі, қанша солға қарай ығысулар жасалса, сонша кері оңға қарай циклдік ығысулар жасалады.

Жұптыққа тексеру әдісі. Егер комбинация бұрмалаусыз қабылданған болса, модуль 2 бойынша бірліктер қосындысы нөлді береді. Әлдебір символ бұрмаланған болса, тексеру кезіндегі қосындылау бірді беруі мүмкін. Әрбір тексерудің қосындылауы нәтижесі бойынша бұрмалану орнын көрсететін екілік сан құрылады.

65. Жұмсақ және қатаң декодалау. Алгебралық және Мажоритарлы декодалау. Кодалау дәрежесі 1/2-ге тең екілік кодтық жүйе үшін демодулятор декодерға бір мезгілде екі кодтық символ береді. Қатаң (екідеңгейлі) декодалау үшін қабылданған кодтық сөздердің әрбір жұбынжазықтықта 7.5,а суретінде көрсетілгендей шаршының бір бұрышы түрінде бейнелеуге болады. Бұрыштар төрт мүмкін болатын мәнді көрсететін (0, 0), (0, 1), (1, 0) және (1, 1) екілік сандармен белгіленген, олар шешім қабылдаудың қатаң сұлбасында екі кодтық символ қабылдай алады. Осыған ұқсас, 8-деңгейлі жұмсақ декодалау үшін кодтық символдардың әрбір жұбын жазықтықта 7.5,б суретінде көрсетілгендей 64 нүктеден тұратын 8x8 өлшемді теңбүйірлі тіктөртбұрыш түрінде бейнелеуге болады. Бұл жағдайда демодулятор ендігі қатаң шешім бермейді; ол шулы кванттық сигналдар береді (шешім қабылдаудың жұмсақ сұлбасы).

Витерби алгоритмі бойынша жұмсақ және қатаң декодалаудың арасындағы негізгі айырмашылық жұмсақ сұлбада онда рұқсат етілу шектеулі болғандықтан, Хэмминг арақашықтығы метрикасы қолданылмайды. Қажетті рұқсат етілуі бар арақашықтық метрикасы евклидтік кодтық арақашықтық деп аталады, сол себепті әрі қарай оның қолданылуын жеңілдету үшін екілік сандарды бірліктер мен нөлдерден 0-ден 7-ге дейінгі сегіздік сандарға сәйкес түрде түрлендіреміз. Мұны 7.5,в суретінде көруге болады, онда шаршының бұрыштары сәйкес түрде белгіленген; енді 64 нүктенің кез-келгенін сипаттау үшін біз 0-ден 7-ге дейінгі бүтін сандар жұбын қолданатын боламыз. 7.5,в суретінде осы секілді шулы кодтық символдардың мәндері жұбының мысалын көрсететін 5,4 нүктесі бейнеленген. 7.6,в суретіндегі шаршы (х,у) координатасында бейнеленген деп елестетейік. 5,4 шулы нүктесі мен 0,0 шусыз нүктесі арасындағы евклидтік кодтық арақашықтық қандай болады? Ол тең. Ал егер біз 5,4 шулы нүктесі мен 7,7 шусыз нүктесі арасындағы евклидтік кодтық арақашықтықты білгіміз келсе ше? Сәйкес .

7.5 сурет – Витерби декодалауы:

а) шешім қабылдаудың қатаң сұлбасының жазықтығы;

б) шешім қабылдаудың жұмсақ сұлбасының 8-деңгейлі жазықтығы;

в) жұмсақ кодтық символдардың мысалы;

г) кодалау торының бөлігі;

д) декодалау торының бөлігі.

Витерби алгоритмі бойынша жұмсақ декодалаудың басым бөлігі қатаң декодалау тәрізді орындалады. Тек бір ғана айырмашылығы, мұнда Хэмминг арақашықтығы қолданылмайды. Сол себепті евклидтік кодтық арақашықтықпен жүзеге асырылатын жұмсақ декодалауды қарастырамыз. 7.5,г суретінде кодалау торының бірінші бөлігі көрсетілген. Бұған қоса, кодтық сөздер екіліктен сегіздікке түрлендірілген. Декодерге бірінші өту кезінде түскен кодтық символдар жұбы декодалаудың жұмсақ сұлбасына сәйкес 5,4 мәніне ие делік. 7.5,д суретінде декодалау торының бірінші бөлігі көрсетілген. 5,4 келіп түскен тармақталған сөзі мен 0,0 тармақталған сөзі арасындағы евклидтік кодтық арақашықтықты көрсететін (√41) метрикасы тұтас сызықпен белгіленген. Осыған ұқсас, (√13) метрикасы 5,4 келіп түскен кодтық символы мен 7,7 кодтық символы арасындағы евклидтік кодтық арақашықтықты көрсетеді; бұл арақашықтық үзік сызықпен көрсетілген. Тордың қиылысуына және толық тармақты іздеуге алып келетін декодалау міндетінің қалған бөлігі қатаң декодалау сұлбасына ұқсас жүзеге асырылады. Үйірткілі декодалау үшін арналған іс жүзіндегі микросхемаларда евклидтік кодтық арақашықтық шын мәнінде қолданылмайды, оның орнына ұқсас қасиеттерге ие, бірақ та жүзеге асырылуы айтарлықтай оңайырақ бір сарынды (монотонды) метрика қолданылады. Мұндай метриканың мысалы болып екі дәрежеленген евклидтік кодтық арақашықтық табылады, онда жоғарыда қарастырылған екі дәрежелі түбір астына алу амалы болмайды. Бұдан басқа, егер екілік кодтық символдар биполярлы шамалармен келтірілген болса, онда скалярлық көбейтілу метрикасын қолдануға болады. Мұндай метрикада минимальді арақашықтықтың орнына біз максимальді түзетулерді қарастыруға тиіс боламыз.

Мажоритарлы декодалау. Бұл әдіс қабылданған кодтық комбинацияның әрбір символын (n,k) циклдік кодының әрбір нұсқасы үшін құрастырылған арнайы коэффициенттер кестелері бойынша бірнеше мәрте тексерумен түйінделеді. әрбір символдың мәні мажоритарлы принцип («мажоритарлы» сөзі көпшілік дегенді білдіреді) бойынша, яғни, дауыс беру принципі бойынша анықталады. Бұл егер, мысалға, берілген символдық тексерудің бестен бірінен үшеуі 1-ді, ал екеуі 0-ді көрсетсе, символға бір мәні меншіктеледі дегенді білдіреді. Егер барлық тексерулер 1 немесе 0 көрсетсе, онда символ бұрмаланбаған деп есептеліп, өзгеріссіз қабылданады.

Егер қандай да бір тексеруде 1 мен 0 саны тең болып қалса, онда бұл берілен код үшін қателердің жөнделмейтін комбинациясы кетті және қабылданған комбинация жарамсыз деп табылуы тиіс дегенді білдіреді.

66. Үйірткілі кодтарды декодалау. Возенкрафт және Фано алгоритмі. Егер хабарлардың барлық кіріс тізбектері тең ықтималды болса, қатенің минимальді ықтималдығы шартты ықтималдықты салыстырып, максимальдісін таңдайтын декодерді қолданғанда болады. Шартты ықтималдықты тағы да Р(Z|U^(m)) шындыққа жанасу функциялары деп те атайды, мұндағы Z – бұл қабылданған тізбек, aл U^(m) – таратылуы мүмкін тізбектердің бірі. Егер барлық U^(m) бойынша

Р(Z|U^(m’)) = max Р(Z|U^(m)) болса, декодер U^(m’)-ді таңдайды (7.36)

(7.36) теңдеуімен анықталатын максимальді шындыққа жанасу принципі шешім қабылдау теориясының іргелі жетістігі болып табылады; бұл ықтималдықтар туралы статистикалық мәліметтер болған кездегі "дұрыс мағынаға" негізделген шешім қабылдау тәсілінің формальдануы. Екілік демодуляцияны қарастырғандатек екі ықтималды s₁(t) және s₂(t) символдарының таратылуы жорамалданған. Демек, берілген қабылданған сигналға қатысты максимальді шындыққа жанасу принципі негізінде екілік шешімді қабылдау егер төмендегі шарт орындалса, таратылған сигнал ретінде s₁(t) таңдалады дегенді білдіреді

(7.37)

Олай болмаған жағдайда s₂(t) сигналы таратылды деп есептеледі. z параметрі z(T) шамасын көрсетеді, символды таратудың әрбір периоды соңындағы детекторлауға дейінгі қабылданған сигналдың мәні t = T. Алайда үйірткілі декодалауда максимальді шындыққа жанасу принципін қолдану кезінде үйірткілі кодта жады барлығы анықталады (алынған тізбек ағымдағы және оның алдындағы екілік разрядтардың суперпозициясы болып табылады). Осылайша, үйірткілі кодпен кодаланған мәліметтер битін декодалау кезінде максимальді шындыққа жанасу принципін пайдалану (7.36) теңдеуінде көрсетілгендей, ең ықтимал тізбекті таңдау контекстінде жүзеге асырылады. Әдетте кодтық сөздердің көптеген таратылуы мүмкін тізбектері болады. Екілік кодқа келетін болсақ, онда L тармақталған сөздерінің тізбегі 2^L мүмкін болатын тізбектер жиынтығының мүшесі болып табылады. Демек максимальді шындыққа жанасу контекстінде егер Р(Z|U^(m’)) ықтималдығы барлық қалған таратылуы мүмкін тізбектердің ықтималдығынан көбірек болса,декодер таратылған тізбек ретінде U^(m’)-ді таңдайды деп айтуға болады. Мұндай қателердің ықтималдығын азайтатын (барлық таратылған тізбектер тең ықтималды болғанда) ең тиімді декодер максимальді шындыққа жанасу принципі бойынша жұмыс істейтін декодер (maximum likelihood detector) деген атпен белгілі. Шындыққа жанасу функциясы арнаның спецификациясына сүйене отырып беріледі немесе есептеп шығарылады.

Біз жадысыз арнадағы нөлдік орташалы, яғни шу кодтың әрбір символына басқа символдарға тәуелсіз әсер ететін аддитивті ақ гаустық шумен әрекеттескелі отырмыз делік. Үйірткілі кодтың 1/n-ге тең дәрежесінде шындыққа жанасуды былайша өрнектеуге болады.

(7.38)

Мұндағы Z_i – бұл алынған Z тізбегінің i-ші тармағы, U_i^(m) – бұл U^(m) кодтық сөздерінің бөлек тізбегінің тармағы, z_ij – бұл Z_і-нің j-ші кодтық символы, u_ij – бұл U^(m)-нің j-ші кодтық символы, ал әрбір тармақ n кодтық символдардан тұрады. Декодалаудың міндеті төмендегі көбейтілу максимальді болатындай, 7.6 суретінде көрсетілген тор арқылы өту жолын таңдау болып түйінделеді (әрбір мүмкін болатын жол кодтық сөздер тізбегін анықтайды)

(7.39)

Есептеулер кезінде шындыққа жанасу функциясының логарифмін пайдаланған ыңғайлырақ, себебі бұл көбейтілуді қосындылаумен ауыстыруға мүмкіндік береді. Логарифм бір сарынды (монотонды) өсетін функция болғандықтан, демек, ақырғы кодтық сөзді таңдауға өзгеріс енгізбейтіндіктен, біз осы түрлендіруді пайдалана аламыз. Шындыққа жанасудың логарифмдік функциясын былайша анықтауға болады.

(7.40)

Енді декодалаудың міндеті γ_U(m) максимальді болатындай 7.7 суретінде көрсетілген тор немесе ағашты жағалай өту жолын таңдау болып түйінделеді. Үйірткілі кодтарды декодалау кезінде ағаш тәріздес құрылыммен қатар, торлы құрылымды да қолдануға болады. Кодтың ағаш тәріздес суреттелуінде жолдардың қайта бірігуі ескерілмейді. Екілік код үшін L тармақталған сөздерден тұратын мүмкін болатын тізбектер саны 2^L-ге тең. Сол себепті, ағаш тәріздес диаграманы қолданатын максимальді шындыққа жанасу принципіне негізделген алынған тізбектерді декодалау "өктем күш" немесе мүмкін болатын кодтық сөздер тізбектерінің барлық нұсқаларын сипаттайтын 1^L шындыққа жанасудың жинақталған логарифмдік метрикаларын жан-жақты салыстыру әдісін талап етеді.. Сондықтан, максимальді шындыққа жанасу принципі негізіндегі декодалауды ағаш тәрізді құрылым көмегімен қарастыру іс жүзінде мүмкін емес. Осының алдындағы тарауда кодтың торлы суреттелуінде декодерді максимальді шындыққа жанасатын тізбектің рөліне кандидат бола алмайтын жолдардан бас тарта алатындай етіп құруға болатыны көрсетілді. Декодалау жолы аман қалған жолдардың әлдебір ықшамдалған жиынтығынан таңдап алынады. Мұндай декодер дегенмен де тиімді болып саналады.

7.6 сурет – Кодердің торлы диаграммасы (кодалау дәрежесі ½, К=3)

Возенкрафт және Фано алгоритмі. Бұдан ертерек, Витерби үйірткілі кодтарды декодалаудың тиімді алгоритмін ашқанға дейін, басқа да алгоритмдер болған. Ең бірінші алгоритм Уозенкрафтпен (Wozencraft) ұсынылған және Фаномен (Fano) өзгертілген тізбектеп декодалау алгоритмі болды. Тізбектік декодердің жұмысы барысында кодтық сөздердің таратылған тізбегі туралы болжам генерацияланады да, осы болжам мен қабылданған сигнал арасындағы метрика есептеледі. Бұл процедура әзірге метрика болжамның таңдалуы шындыққа жанасатынын көрсетіп тұрғанша жалғаса береді, олай болмаған жағдайда болжам ең шындыққа жалғасатыны табылғанша тізбектеліп алмастырыла береді. Іздестіру бұл кезде байқап көрулер мен қателесулер әдісімен іске асады. Жұмсақ және қатаң декодалау үшін тізбектік декодер жасап шығаруға болады, бірақ әдетте есептеулердің күрделілігі мен жады талап ететіндігіне бола жұмсақ декодалауды қолданбауға тырысады.

7.7 суретінде бейнеленген кодер қолданылатын, m = 1 101 1 тізбегі U = l 101010001 кодтық сөздер тізбегіне кодаланған жағдайды қарастырайық. Қабылданған Z тізбегі факт жүзінде U тізбегінің дұрыс таратылуы делік. Декодерде кодтық ағаштың көшірмесі болады да ол ағаштан өту үшін қабылданған Z тізбегін пайдалана алады. Декодер t₁ сәтіндегі ағаш түйінінен бастайды да, осы түйіннен шығатын екі жолды да генерациялайды. Декодер алынған және кодтық символдармен келісілген жолмен жүреді. Ағаштың келесі деңгейінде декодер тағы да түйіннен шығатын екі жолды генерациялайды да, символдардың екінші тобымен келісілген жолмен жүреді. Осыған жалғастыра отырып, декодер барлық ағашты іріктеп шығады.

Енді қабылданған Z тізбегі бұрмаланған U кодтық сөзі болып табылады делік. Декодер t₁ сәтіндегі ағаш түйінінен бастайды да, осы түйіннен шығатын екі жолды да генерациялайды. Егер қабылданған n кодтық символдар генерацияланған жолдардың біреуімен дәл келетін болса, декодер осы жолмен жүреді. Егер сәйкестік жоқ болса, декодер ең ықтимал жолмен жүреді, бірақ бұған қоса қабылданған символдар мен жүру жолдарындағы тармақталған сөздер арасындағы сәйкессіздіктердің жалпы есептеуін жүргізеді. Егер екі тармақ та тең ықтималды болса, онда қабылдағыш нөлдік кіріс жолы болған жағдайдағыдай еркін таңдау жасайды. Ағаштың әрбір деңгейінде декодер жаңа тармақтар генерациялайды да оларды n қабылданған кодтық символдардың келесі жиынтығымен салыстырады. Іздестіру әзірге барлық ағаш ең ықтимал жолмен жүріп өтілмейінше жалғаса береді, және бұған қоса сәйкессіздіктердің есебі жасалады.

Егер сәйкессіздіктердің есебі белгілі бір саннан асып кетсе (ол ағаштан өткен соң ұлғаюы мүмкін), декодер дұрыс емес жолдамын деп есептейді де, бұл жолды алып тастайды да бәрін қайтадан қайталайды. Декодер келесіде ағаштан өткенде оларға жоламайтын мүмкіндік болуы үшін алып тасталған жолдардың тізімін жадында сақтайды. 7.7 суретінде келтірілген кодер m = 11011 ақпараттық тізбегін U кодтық сөздер тізбегіне кодалайды делік. U таратылған тізбегінің төртінші және жетінші биттері қатемен қабылданған деп жорамалдайық.

Уақыт t₁ t₂ t₃ t₄ t₅

Ақпараттық тізбек: m = 1 1 0 I 1

Таратылған тізбек: U = 11 01 01 00 01

Қабылданған тізбек: Z = 11 00 01 10 01