2.3.1 Резонанс напруг

R L Xl C Xc

Ua=Ur Ul Uc

U I

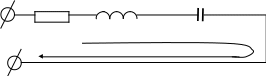
Рисунок 2.6 – Коло з послідовним з’єднанням R, L, C

Умовою виникнення резонансу напруг є рівність реактивних опорів .

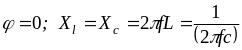Характерні особливості резонансу

1. Сумарний опір 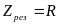, оскільки 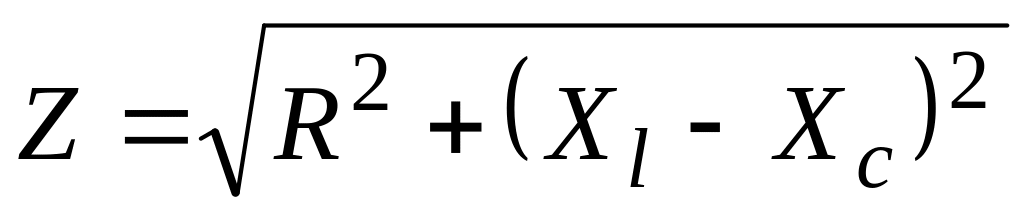, то загальний опір під час резонансу мінімальний, бо .

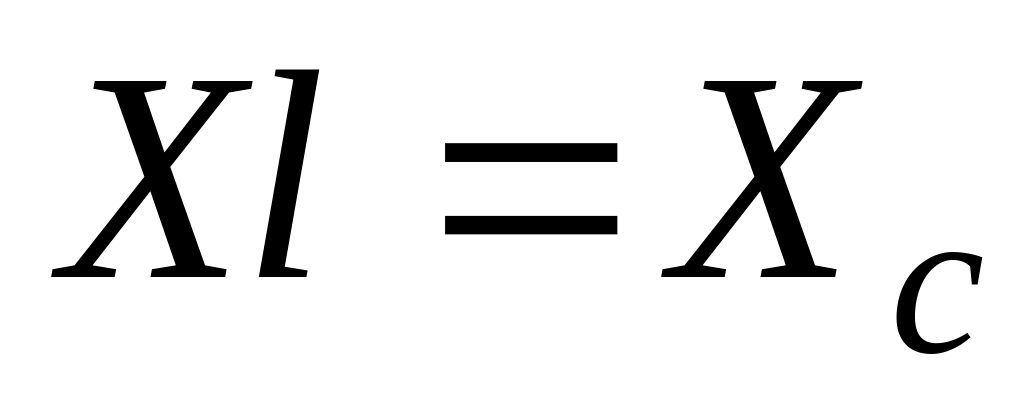2. Коефіцієнт потужності .

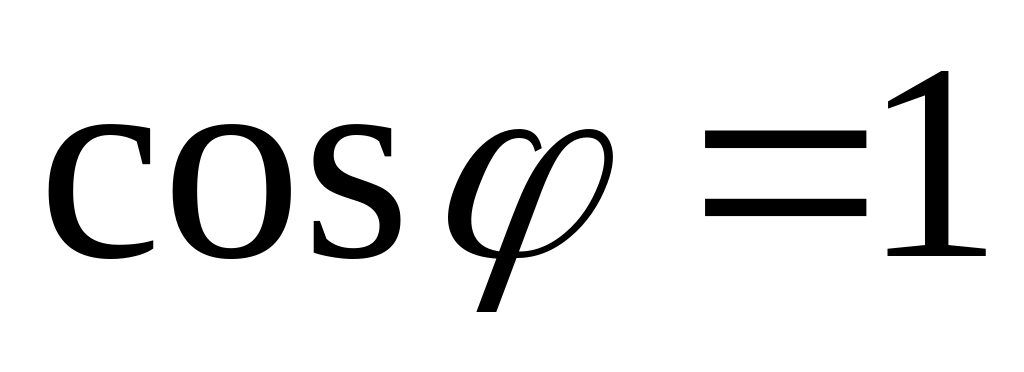3. Струм під час резонансу максимальний – .

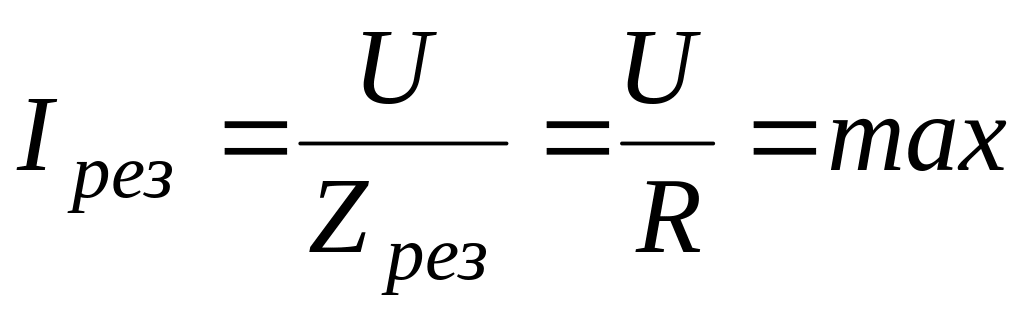Резонансний струм (рис. 2.6) за певних умов небезпечний, він максимальний, може спричинити пошкодження елементів кола та вивести їх із ладу. Оскільки при резонансі , то (напруга мережі живлення). Резонанс напруг – шкідливе явище. У реальних умовах його намагаються не допустити. Векторна діаграма режиму резонансу зображена на рисунку 2.7.

w – завжди проти руху

U_l годинникової

стрілки

w

0 Ur = Ua I

U_c

Рисунок 2.7 – Векторна діаграма кола з послідовним з’єднанням R, L, C

Для режиму резонансу характерні ще такі зміни опору (рис. 2.8):

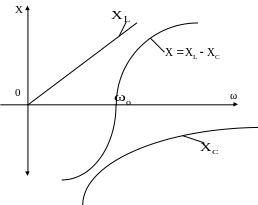
Рисунок 2.8 – Зміна опору кола з послідовним з’єднанням R, L, C

Зміна струму показана на рисунку 2.8.

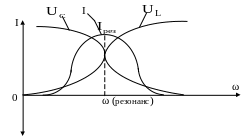
Рисунок 2.9 – Зміна струму кола з послідовним з’єднанням R, L, C

2.3.2 Резонанс струмів

Виникає в колах із паралельним з’єднанням елементів (рис. 2.10).

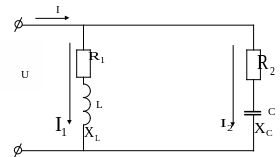
Рисунок 2.10 – Коло з паралельним з’єднанням R, L, C

Для резонансу струмів (рис. 2.11 – 2.13):

Умовою резонансу струмів є В_L = Bc (рівність реактивних провідностей паралельних гілок); B = 1/X[Ом^-1] (сименс).

Характерні особливості резонансу струмів:

1. Опір кола практично активний і максимальний: Z = R = max.

1. Струм у нерозгалуженій частині кола мінімальний:

І = min – це дуже добре!

2. Q _L = Qc (реактивні потужності приблизно рівні). Це означає, що, як і при резонансі напруг, між котушкою і конденсатором відбувається обмін енергією, але джерело живлення в цьому процесі участі не бере.

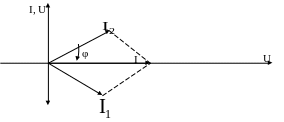
Рисунок 2.11 – Векторна діаграма кола з паралельним з’єднанням R, L, C

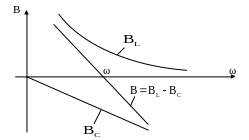
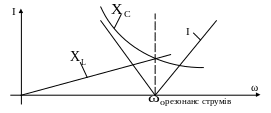
Рисунок 2.12 – Зміна провідності кола з паралельним з’єднанням R, L, C

Рисунок 2.13 – Зміна векторних величин кола з паралельним з’єднанням R, L, C