
Задача 3
Фирма производит пользующиеся спросом детские платья и костюмы, реализация которых зависит от состояния погоды. Затраты фирмы в течение апреля-мая на единицу продукции составят: платья – А ден. ед., костюмы – В ден. ед. Цена реализации составит С ден. ед. и D ден. ед. соответственно.
По данным наблюдений за несколько предыдущих лет, фирма может реализовать в условиях теплой погоды Е шт. платьев и К шт. костюмов, при прохладной погоде – М шт. платьев и N шт. костюмов.
В связи с возможными изменениями погоды определить стратегию фирмы в выпуске продукции, обеспечивающую ей максимальный доход.
Задачу 3 решить графическим методом и с использованием критериев игр с природой, приняв степень оптимизма α.
A =5, B = 25, C = 10, D = 40, E = 1220, K = 550, M = 410, N = 930, α= 0,4
Решение
1. Фирма располагает двумя стратегиями:
а1 – в этом году будет теплая погода; а2 – в этом году будет холодная погода.
Если фирма примет стратегию а1 и в действительности будет теплая погода (стратегия природы b1), то выпущенная продукция (1220 шт. платьев и 550 шт. костюмов) будет полностью реализована и доход составит:
1220(10 – 5) + 550(40 – 25) = 14350 ден. ед.
В условиях прохладной погоды (стратегия природы b2) костюмы будут проданы полностью, а платья только в количестве 410 шт. и часть платьев останется нереализованной. Доход составит:
410(10 – 5) + 550(40 – 25) – 5 · (1220 – 410) =6250 ден. ед.
Если фирма примет стратегию а2 и в действительности будет холодная погода, то доход составит: 410(10 –5) + 930(40 – 25) = 16000 ден. ед.
При теплой погоде доход составит:
410(10 –5) + 550(40 – 25) – 25 · (930 – 550) =800 ден. ед.
Рассматривая фирму и погоду в качестве
двух игроков, получим платежную матрицу:
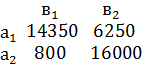
сa = max(6250, 800) = 6250 ден. ед.
сb = min(14350, 16000) = 14350 ден. ед.
Цена игры лежит в диапазоне 6250 ≤ v ≤ 14350 ден. ед.
Найдем решение игры графическим методом. Обозначим:
х1 – вероятность применения фирмой стратегии а1;
х2 – вероятность применения фирмой стратегии а2;
х2 = 1 – х1 .
Определим ожидаемые выигрыши первого игрока при применении вторым игроком стратегий b1 и b2 по формуле (w1n – w2n) · х1 + w2n.
(14350 – 800) · х1 + 800 = 13550 х1 + 800
(6250 – 16000) · х1 + 16000 = -9750 х1 + 16000
Составим таблицу:
Таблица 8
Чистые стратегии второго игрока |
Ожидаемые выигрыши первого игрока |
b1 |
13550 х1 + 800 |
b2 |
-9750 х1 + 16000 |
На оси Х1 разместим точки х1 = 0 и х1 =1, через которые проведем прямые, перпендикулярные оси Х1. Подставляя х1 = 0 и х1 =1 в выражение 13550 х1 + 800, найдем значения, которые отложим на соответствующих перпендикулярных прямых:
х1 = 0: 13550 · 0 + 800 = 800;
х1 = 1: 13550 · 1 + 800 = 14350.
Соединив точки 800 и 14350, получим прямую.
Аналогично рассмотрим выражение -9750 х1 + 16000:
х1 = 0: -9750 · 0 + 16000 = 16000;
х1 = 1: -9750 · 1 + 16000 = 6250. Соединяем точки 16000 и 6250.
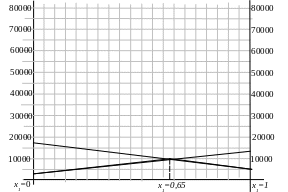
Рис. 3.
Для определения оптимальной стратегии фирмы приравняем уравнения, чтобы найти точку пересечения: 13550х1 + 800 = -9750 х1 + 16000,
23300х1 = 15200, х1 = 0,65; х2 = 1 – 0,65 = 0,35.
Оптимальная стратегия фирмы
![]() =
(0,65; 0,35)
=
(0,65; 0,35)
Цена игры: v = 13550 х1 + 800 = 13550 · 0,653 + 800 = 9607,5 ден. ед.
Оптимальный план выпуска продукции:
0,65 · (1220; 550) + 0,35 · (410; 930) = (936,5; 683).
Таким образом, в течение апреля-мая фирма должна произвести
936,5 шт. платьев и 683 шт. костюмов, тогда при любой погоде она получит доход не менее 9607,5 ден. ед.
2. Решим задачу с использованием критериев игр с природой.
а) Критерий Вальде: max(min wij) = max(6250, 800) = 6250 ден. ед.,
фирме целесообразно использовать стратегию а1.
б) Критерий максимума: max(max wij) = max(14350, 16000) = 16000 ден. ед.,
фирме целесообразно использовать стратегию а2.
в) Критерий Гурвица:
для стратегии фирмы а1
α min wij + (1 – α ) max wij = 0,4 ·6250 + (1 – 0,4) · 14350 = 11110 ден. ед.,
для стратегии фирмы а2
α min wij + (1 – α ) max wij = 0,4 · 800 + (1 – 0,4) · 16000 = 9920 ден. ед.,
max(11110, 9920) = 11110 ден. ед.
По критерию Гурвица фирме целесообразно использовать стратегию а2.
г) Критерий Сэвиджа.
Максимальный элемент в первом столбце – 6250, во втором столбце – 16000.
Элементы матрицы рисков находятся из выражения: rij = max wij – wij , откуда
r11 = 6250 – 6250 = 0, r12 = 16000 – 6250 = 9750,
r21 = 6250 – 800 = 5450, r22 = 16000 – 16000 = 0.
Получаем матрицу рисков: ![]()
min{max (max wij – wij )} = min(9750, 5450) = 5450 ден. ед.,
По критерию Сэвиджа фирме целесообразно использовать стратегию а2.
Таким образом, по одному критерию фирме целесообразно использовать стратегию а2, по трем критериям целесообразно использовать стратегию а1; следовательно, фирме целесообразно применять стратегию а2.
