10

КОНТРОЛЬНАЯ РАБОТА по ДИСЦИПЛИНЕ "ТЕОРИЯ ИГР"

Студентки Антошуки Анным Васильевны, гр. 2012-З-ФК 1

Вариант 1

ЗадаЧА 1

Найти оптимальные стратегии и цену игры, заданной платежной матрицей

Решение

Проверим, имеет ли игра седловую точку. Найдем верхнюю и нижнюю цены игры.

минимумы по строкам

3	4	5	2	2
7	6	4	8	4	– максимальный из них

_{м аксимумы по столбцам 7 6 5 8}

минимальный

Таким образом, с_a = 4, c_b = 5, с_a ≠ c_b , игра не имеет седловой точки.

Оптимальное решение следует искать в области смешанных стратегий. Цена игры должна удовлетворять условию: 4 ≤ v ≤ 5.

Обозначим:

х₁ – вероятность применения первым игроком 1-й стратегии;

х₂ – вероятность применения первым игроком 2-й стратегии; х₁ + х₂ = 1;

у₁ – вероятность применения вторым игроком 1-й стратегии;

у₂ – вероятность применения вторым игроком 2-й стратегии;

у₃ – вероятность применения вторым игроком 3-й стратегии;

у₄ – вероятность применения вторым игроком 4-й стратегии; у₁+у₂+у₃+у₄=1.

Найдем ожидаемые выигрыши первого игрока при применении вторым игроком 1, 2, 3, 4-й стратегий по формулам (w_1n – w_2n)·х₁ + w_2n. Данные занесем в таблицу 1:

Таблица 1

Чистые стратегии второго игрока	Ожидаемые выигрыши первого игрока
1	-4х1 + 7
2	-2х1 + 6
3	х1 + 4
4	-6х1 + 8

Найдем решение игры графическим методом (рис. 1). На оси Х₁ разместим точки х₁ = 0 и х₁ =1, через которые проведем прямые, перпендикулярные оси Х₁. Подставляя х₁ = 0 и х₁ =1 в выражение -4х₁ + 7, найдем значения, которые отложим на соответствующих перпендикулярных прямых:

х₁ = 0: -4 · 0 + 7 = 7;

х₁ = 1: -4 · 1 + 7 = 3. Соединив точки 7 и 3, получим прямую.

Аналогично рассмотрим выражение -2х₁ + 6:

х₁ = 0: -2 · 0 + 6 = 6;

х₁ = 1: -2 · 1 + 6 = 4. Соединяем точки 6 и 4.

Выражение х₁ + 4:

х₁ = 0: 0 + 4 = 4;

х₁ = 1: 1 + 4 = 5. Соединяем точки 4 и 5.

Выражение -6х₁ + 8:

х₁ = 0: -6 · 0 + 8 = 8;

х₁ = 1: -6 · 1 + 8 = 2. Соединяем точки 8 и 2.

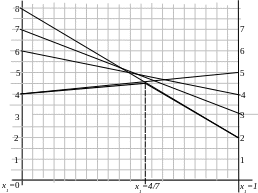
Рис. 1.

Нижняя огибающая – это пересечение нескольких прямых; выше других пересекаются прямые х₁ + 4 и -6х₁ + 8.

Приравняем эти выражения, чтобы найти точку пересечения:

х₁ + 4 = -6х₁ + 8, 7х₁ = 4,

х₁ = 4/7 х₂ = 1 – х₁ = 3/7.

Цена игры равна: v = х₁ + 4 = 4/7 + 4 = 32/7.

Оптимальная стратегия первого игрока: , при этом цена игры v = .

Найдем оптимальную стратегию для второго игрока.

Из чертежа мы установили, что оптимальная стратегия первого игрока определяется из равенства выражений х₁ + 4 и -6х₁ + 8, что соответствует 3-й и 4-й чистым стратегиям второго игрока. Это означает, что у₁ = у₂ = 0, а

У₄ = 1 – у₃.

Ожидаемые проигрыши второго игрока при применении первым игроком своих стратегий составят:

(w₁₃ – w₁₄) · y₃ + w₁₄ = (5 – 2) · y₃ + 2 = 3y₃ + 2

(w₂₃ – w₂₄) · y₃ + w₂₄ = (4 – 8) · y₃ + 8 = -4y₃ + 8

Полученные данные занесем в таблицу 2:

Таблица 2

Чистые стратегии первого игрока	Ожидаемые проигрыши второго игрока
1	3у3 + 2
2	-4у3 + 8

Находим координаты: у₁ = 0: 3 · 0 + 2 = 2;

у₁ = 1: 3 · 1 + 2 = 5. Соединяем точки 2 и 5.

у₁ = 0: -4 · 0 + 8 = 8;

у₁ = 1: -4 · 1 + 8 = 4. Соединяем точки 8 и 4.

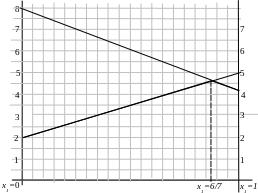
Рис. 2.

Для определения оптимальной стратегии второго игрока приравняем выражения:

3у₃ + 2 = -4у₃ + 8, 7у₃ = 6, у₃ = у₃ = 1 – у₄ = v = 3у₃ + 2 = 3 · + 2=

Оптимальная стратегия второго игрока: , при этом цена игры v = .

Ответ: , , v = .