- •Формальное описание алгоритма 1 задачи “Ближайшая пара”
- •Лекция 2 Задача о битоническом пути
- •Битонический путь
- •Лекция 3 Динамическое программирование и оптимизационная задача перемножения матриц.
- •2. Алгоритмизация описанного процесса на основе (2) и (3).
- •Лекция 4 Оптимальная триангуляция треугольника.
- •Лекция 5
- •Циркуляция.
- •Лекция 6 Многополюсные максимальные потоки
- •Алгоритм гомори—ху
- •Лекция 7 Задача распределения капитала
- •1. Случай запрета коротких позиций.
- •2. Случай разрешения коротких позиций.
- •Случай наличия безрискового актива.
- •Лекция 8 Потоковые алгоритмы.
- •Лекция 9. Алгоритм Гомори.
- •Лекция 10 Многополюсные минимальные потоки.
- •Лекция 11 доминирующие множества и абсолютный центр.
- •Доминирующие множества.
- •Нахождение абсолютного p-центра
- •Ленкция 12 простой (классический) генетический алгоритм.
- •Лекция 13 Стохастическая задача размещения-распределения объектов.
Лекция 6 Многополюсные максимальные потоки
Существует большой ряд технических и экономических задач, в которых рассматриваемые системы могут быть приближенно описаны в виде детерминированных многополюсных потоковых моделей. Примерами таких систем являются: 1) транспортные сети, где автострады изображаются дугами, пропускные способности которых соответствуют максимально допустимой интенсивности движения; 2) телефонные сети, где телефонные линии представляются дугами, а пропускные способности соответствуют максимальному числу вызовов, которые могут обслуживаться в каждый момент времени; 3) электроэнергетические распределительные системы, где линии электропередачи представлены дугами, а пропускные способности соответствуют максимальному объему электроэнергии, который может передаваться по линиям в единицу времени. Во всех этих задачах предполагается существование нескольких источников некоторого продукта. Предполагается также, что величина продукта, который может транспортироваться к нескольким стокам, ограничена только пропускными способностями распределительных звеньев.
Рассмотрим неориентированную сеть с ограниченной пропускной способностью, т. е. сеть, в которой потоки по дугам не должны превосходить пропускных способностей соответствующих дуг. Рассмотрим задачу нахождения максимального потока для всех пар вершин в неориентированной сети. Данную задачу можно рассматривать как обобщение задачи с одним источником и одним стоком, и для ее решения можно воспользоваться методом Форда-Фалкерсона, применяя его к каждой паре вершин. Таких задач равно п (п—1)/2, где п — число вершин в сети Более эффективный метод был предложен Гомори и Ху [1]. На лекции используются основные результаты, полученные в работе [1], и дается обоснование алгоритма. При работе алгоритма Гомори — Ху максимальный поток определяется только п—1 раз.
В дальнейшем будем пользоваться следующим результатом.
Утверждение 1. Для того, чтобы остов взвешенного графа с весовой функцией c был максимальным, н. и д., чтобы для каждого ребра (i,j), не принадлежащего остову, выполнялось условие:
![]() ,
(1)
,
(1)
где![]() - цепь в остове, соединяющая i
и j.
- цепь в остове, соединяющая i
и j.
Алгоритм гомори—ху
Пусть G=(X, U)—неориентированный граф, где X — множество вершин, U — множество дуг. Пусть с(i,j) — пропускная способность дуги (i, j) из множества U, и пусть с(i,j) = с(j,i). Предположим также, что множество вершин задается в виде X={1, 2, ... ..., п}. При описании алгоритма будут использоваться следующие обозначения:
![]() — величина
максимального потока между вершинами
i
и
j;
— величина
максимального потока между вершинами
i
и
j;
![]() — минимальный
разрез, отделяющий i
от j
;
— минимальный
разрез, отделяющий i
от j
;
![]() —
пропускная
способность минимального разреза,
отделяющего i
от
j.
—
пропускная
способность минимального разреза,
отделяющего i
от
j.
Введем функцию v(i,j):= , определенную на множестве ребер. Таким образом, функция v является симметрической: v(i, j)=v(j, i). Будем называть v функцией величины потока на G, или, короче, потоковой функцией. Возникает вопрос, при каких условиях, симметрическая функция v может быть реализована в качестве потоковой функции некоторой сети
Лемма 1. Если v — потоковая функция в некоторой сети, то для любых троек вершин i,j,k
![]() .
(2)
.
(2)
Замечание. Из (2) следует, что из 3-х чисел два должны быть равны, а одно не меньше равных. Полагая v(i,i) = ∞, исключаем требование, чтобы вершины были различны.
Доказательство.
Согласно теореме о максимальном потоке
и минимальном разрезе
![]()
Тогда
либо вершина
![]() и
и
![]() ,
либо вершина
,
либо вершина
![]() и
и
![]() .
И условие (2) выполнено.
.
И условие (2) выполнено.
Из
(2) по индукции следует , что для любого
подмножества вершин
![]() выполнено:
выполнено:
![]() (3)
(3)
Л е м м а 2. Если неотрицательная симметрическая функция v удовлетворяет условию (2) для всех i,j,k, то существует неориентированная сеть, имеющая потоковую функцию V.
Доказательство. Поставив каждой неупорядоченной паре (i,j) в соответствие число v (i, j), мы получим неориентированный граф, каждое из ребер которого имеет «длину» v (i, j). Пусть тогда Т — некоторое макси-
мальное
дерево-остов этого графа. Из (1) и (3)
следует, что если![]() цепь в дереве T
, то
цепь в дереве T
, то
![]()
Поэтому если теперь каждому ребру в дереве приписать пропускную способность с(i, j)= v (i, j), а каждое ребро вне дерева удалить из сети, то сеть Т будет иметь потоковую функцию v. Таким образом, если функция v реализуема, то она реализуема некоторым деревом. , и поэтому она может принимать не более n—1 различных значений, где т — число вершин данного графа.
Рассуждения этого пункта мы можем резюмировать теоремой.
Теорем. Неотрицательная симметрическая функция v реализуема в качестве потоковой функции некоторой неориентированной сети в том и только в том случае, когда она удовлетворяет условию (1). Если функция V реализуема, то она реализуема деревом.
Две сети с n вершинами мы будем называть потоково-эквивалентными, или просто эквивалентными, если они
имеют одну и ту же потоковую функцию v. Таким образом, каждая сеть эквивалентна некоторому дереву.
Если
некоторую вершину s
рассматривать как источник, а другую
вершину t
—
как сток, то, согласно теореме о
максимальном потоке и минимальном
разрезе,
![]() .
Если
затем в качестве источника и стока
выбирается другая пара вершин (i
и
j
соответственно),
удовлетворяющих условию
.
Если
затем в качестве источника и стока
выбирается другая пара вершин (i
и
j
соответственно),
удовлетворяющих условию
![]() или
или
![]() ,
,
то
в алгоритме Гомори — Ху при определении
величины
используется
решение задачи о максимальном потоке,
найденное на предыдущем шаге. А именно,
если
,
то множество вершин
![]() объединяется в одну вершину w
(склеивание, сжатие). Строится
вспомогательный (w-сжатый)
граф
объединяется в одну вершину w
(склеивание, сжатие). Строится
вспомогательный (w-сжатый)
граф
![]() ,
где
,
где
![]() ,
,
![]() .
Пропускные способности дуг вида (i,w)
вычисляются по формуле:
.
Пропускные способности дуг вида (i,w)
вычисляются по формуле:
![]()
При этом величина максимального потока из i в j будет одной и той же для исходной и для конденсированной сетей.
Лемма 3. Величина максимального потока v(i,j) между двумя вершинами i, j сжатой сети равна величине максимального потока v(i, j) в первоначальной сети G=(X, U).
Доказательство.
Пусть
![]() минимальный разрез, отделяющий i
и j
в первоначальной сети
G=(X,
U).
минимальный разрез, отделяющий i
и j
в первоначальной сети
G=(X,
U).
Определим
множества
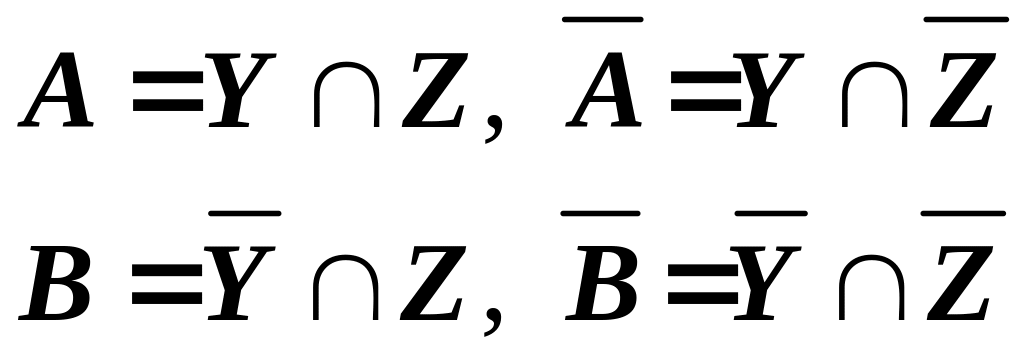
Можем
считать, что i,
s
X
, j
![]()
Случай
1.
![]() .
.
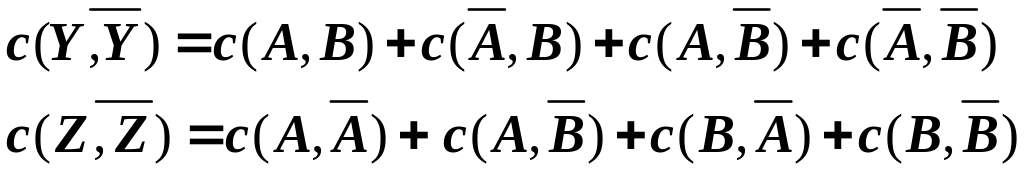
Т.к.
разрез
![]() также отделяет i,j,
то
также отделяет i,j,
то
![]() (4)
(4)
Разрез
![]() также отделяет s,t,
то
также отделяет s,t,
то
![]() (5)
(5)
Складывая
(4) и (5), видим, что
![]() ,
и по-
,
и по-
этому
![]() .
Из (4) и (5) тогда_ следует, что
.
Из (4) и (5) тогда_ следует, что
![]() Значит,
Значит,
![]() также есть минимальный разрез, отделяющдий
i
и j
также есть минимальный разрез, отделяющдий
i
и j
Случай
2.
![]() аналогично.
аналогично.
Итак,
всегда существует минимальный разрез,
отделяющий i
и j
, такой, что множество узлов
![]() лежит
по одну сторону от этого разреза.
Следовательно, сжатие множества
в одну вершину не влияет на величину
максимального потока из i
в j
.
лежит
по одну сторону от этого разреза.
Следовательно, сжатие множества
в одну вершину не влияет на величину
максимального потока из i
в j
.
Основная идея алгоритма состоит в итеративном построении максимального остовного дерева, ветви которого соответствуют разрезам, а параметры ветвей — величинам разрезов.
ОПИШЕМ АЛГОРИТМ.
Произвольным образом выберем два вершины i,j и решим задачу о максимальном потоке между ними. При этом решении будет выделен минимальный разрез который мы символически будем изображать двумя вершинами Y и , соединенными ребром пропускной способности . В одном узле перечисляются все вершины множества Y, а в другом — множества . Затем выберем две вершины , скажем в Y, и решим задачу о максимальном потоке между этими вершинами в -сжатой сети. Получающийся в результате минимальный разрез имеет пропускную способность V2 и изображается ребром этой пропускной способности, соединяющим две части, на которые разбивается множество Y этим разрезом, скажем Y1 и Y2. Если узел принадлежит к той же части разреза, что и Y1 , то прикрепляем его к Y1, а в противном случае к Y2. Этот процесс продолжаем дальше. На каждом этапе построения из диаграммы дерева на этом этапе выбираем некоторое множество Y, состоящее более чем из одной вершины. В этом дереве имеется некоторое количество ребер, инцидентных Y. Все врешины (множества) , которые можно достичь из Y , для следующей задачи о максимальном потоке сожмем в единственный узел. В получившейся сети решим задачу о максимальном потоке между какими-нибудь двумя вершинами множества Y. Найденным при этом решении минимальным разрезом множество Y разобьется на Y1 и Y2. Он (разрез) изображается на новом дереве ребром, соединяющим Y1 и Y2 и имеющим пропускную способность, равную пропускной способности разреза. Остальные вершины старой сети прикрепляются к У1 если они лежат в части разреза, содержащей Y1 и к Y2 в противном случае.
Для формального описания алгоритма используем следующие условия:
Множества Y ( ), если они не одноэлементные, будем помещать в стек, последовательно их нумеруя, начиная с n+1.
Стек представляет собой последовательность записей <numS, S>, где numS – номер множества, S –множество вершин.
w-сжатый граф
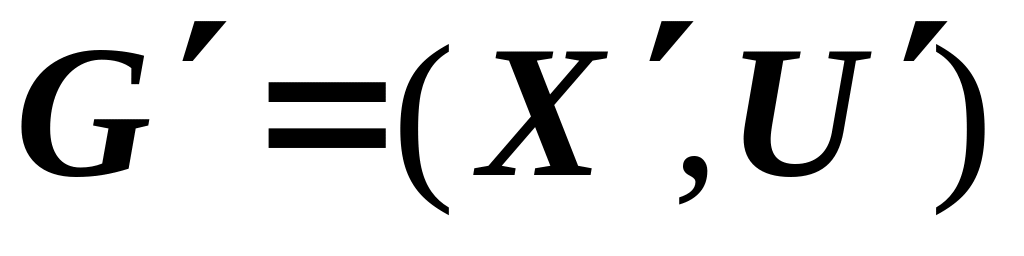 будем задавать матрицей пропускных
способностей
будем задавать матрицей пропускных
способностей
 .
Множество
X’=S{w},
U’={(i,j)U|
i,jS}
{(i,j)U|
iS
& jS}
.
Множество
X’=S{w},
U’={(i,j)U|
i,jS}
{(i,j)U|
iS
& jS}
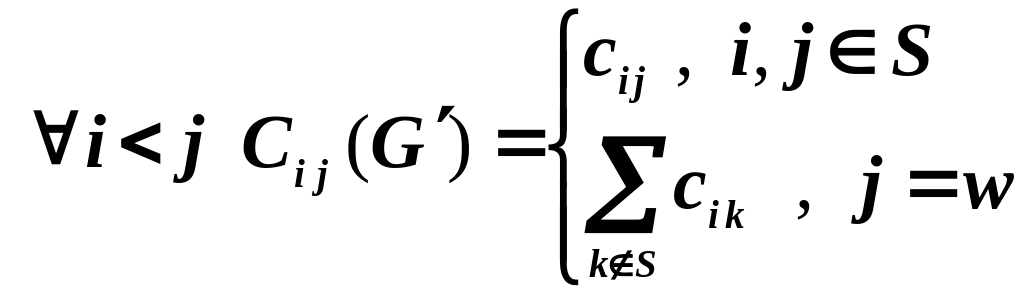
![]()
Дерево задавать списком ребер и их пропускных способностей
Пусть для пары <numS, S> в графе построен минимальный разрез
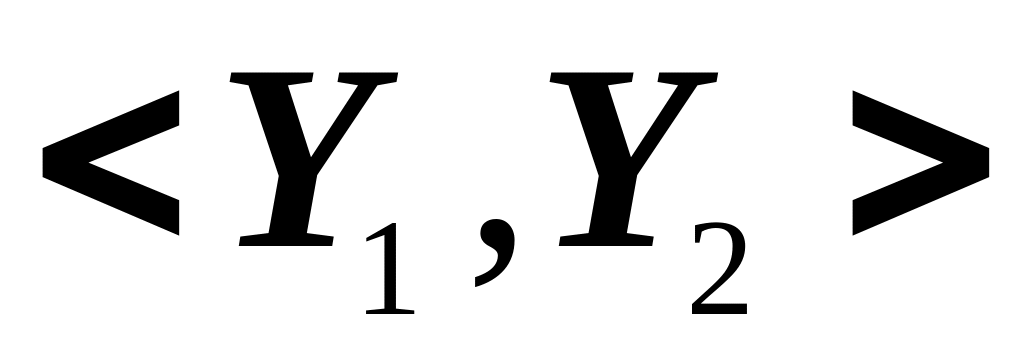 пропускной способности v.
Если
пропускной способности v.
Если
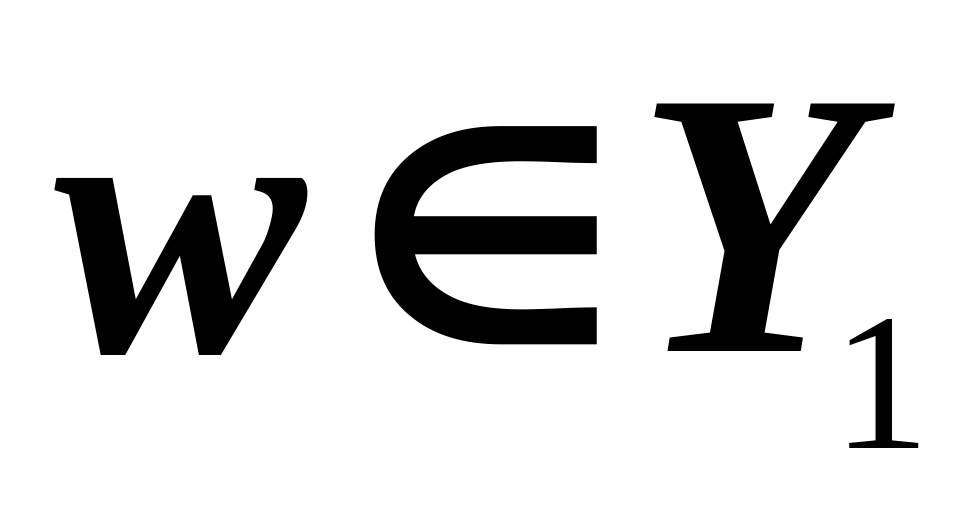 ,
то вычислить
,
то вычислить
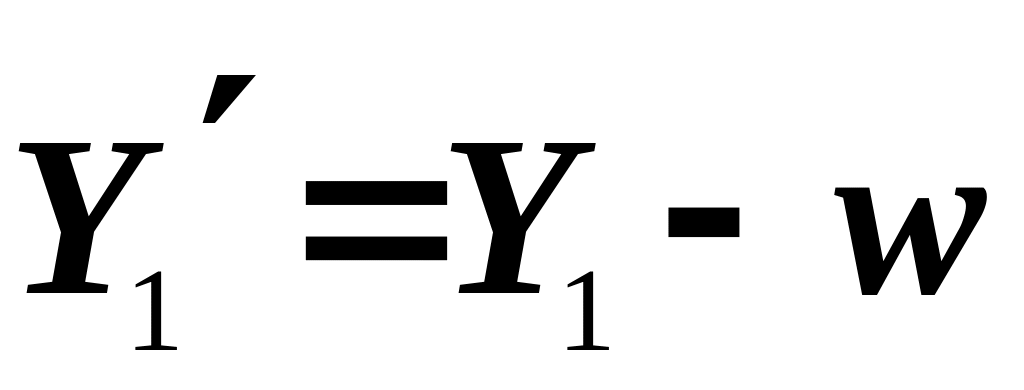 ,
найти номер k:=num(
,
найти номер k:=num(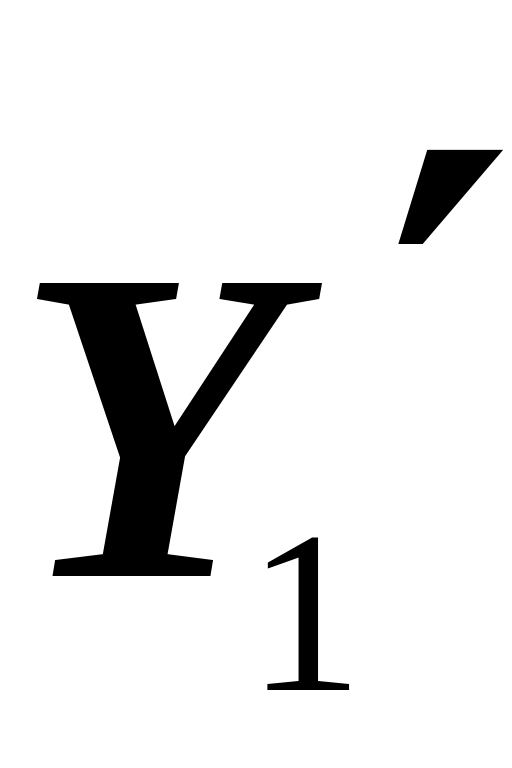 ),
заменить в дереве вершину numS
на k,
пополнить список ребер дерева новым
ребром <k,
num(
),
заменить в дереве вершину numS
на k,
пополнить список ребер дерева новым
ребром <k,
num(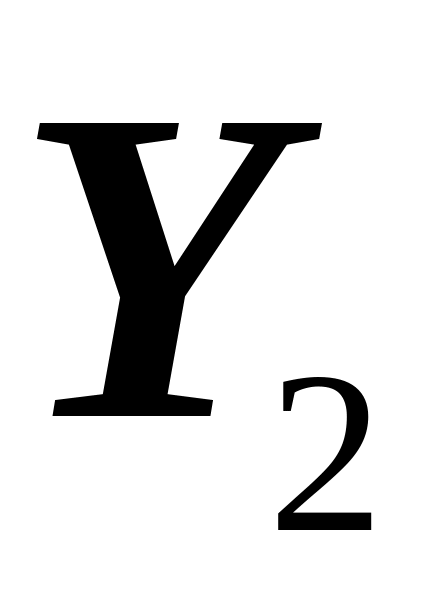 ),
v>.
Если
),
v>.
Если
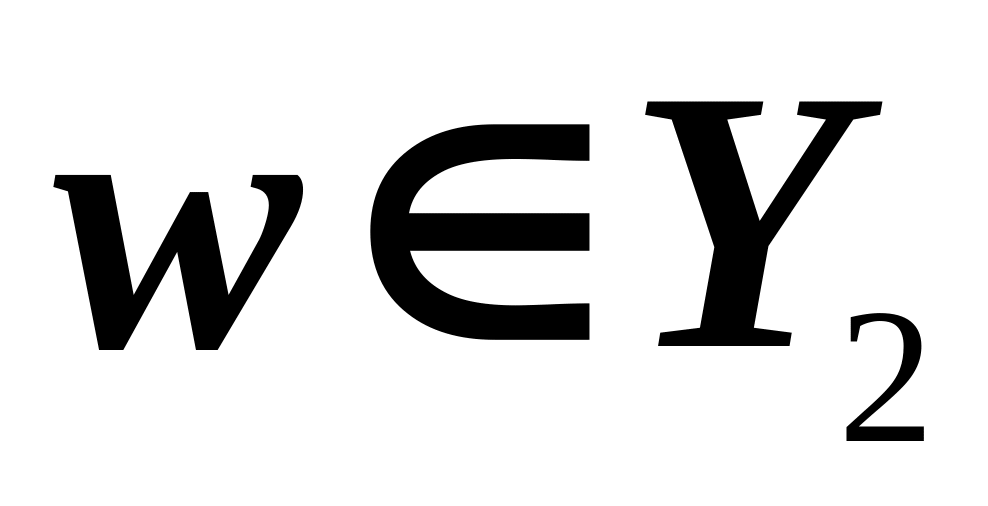 ,
то вычислить
,
то вычислить
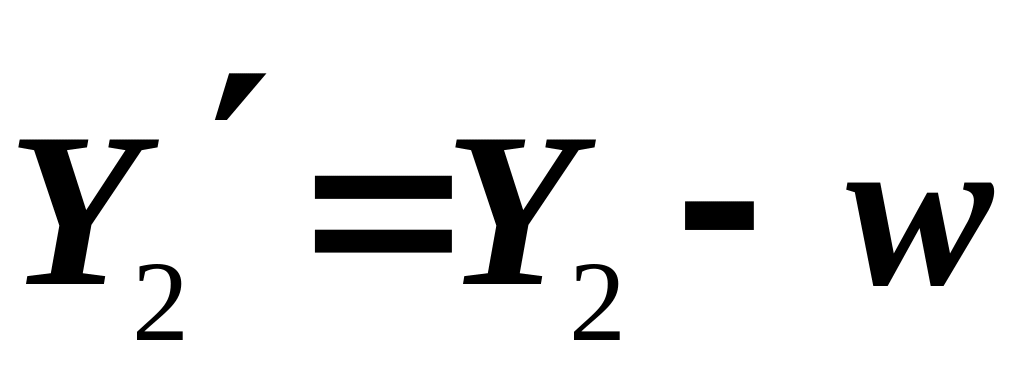 ,
найти номер k:=num(
,
найти номер k:=num(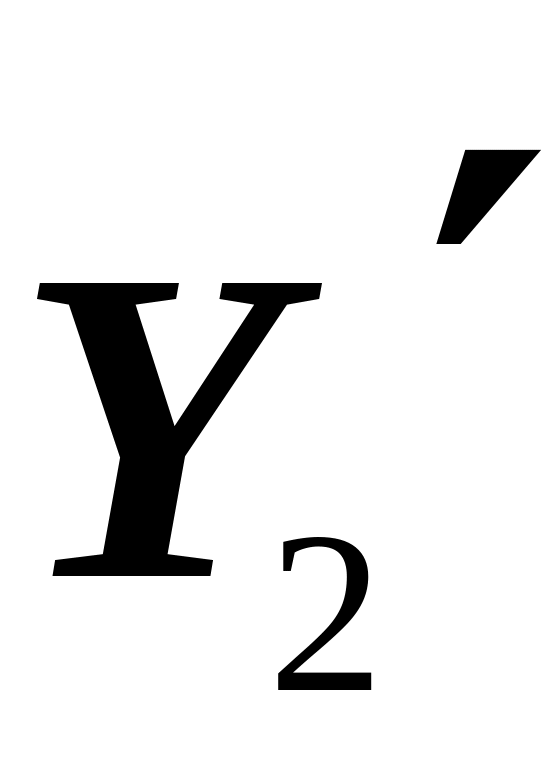 ),
заменить в дереве вершину numS
на k,
пополнить список ребер дерева новым
ребром <k,
num(
),
заменить в дереве вершину numS
на k,
пополнить список ребер дерева новым
ребром <k,
num(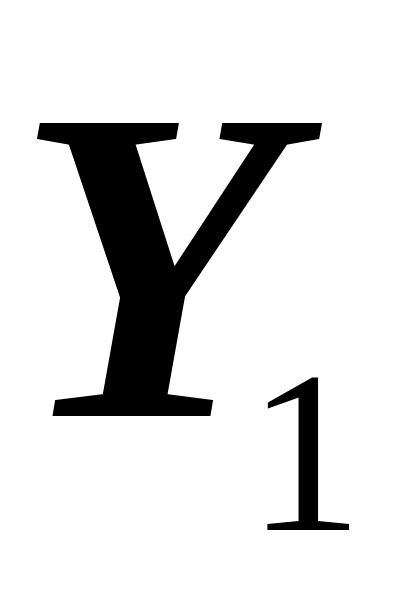 ),
v>.
),
v>.Функция num(S) возвращает номер вершины, если |S| =1, либо номер новой вершины-множество (счетчик) в противном случае.
Докажем, что построенное таким путем дерево T эквивалентно первоначальной сети G.
Л
е м м а 4. Величина максимального потока
между любыми двумя вершинами
![]() первоначальной
сети G
равна
первоначальной
сети G
равна
(6)
где цепь в последнем дереве T.
Доказательство.
Любое ребро u
дерева T
соответствует (согласно алгоритму)
разрезу
![]() ,
где
,
где
![]() множества вершин двух компонент связности
графа T-u.
Этот разрез отделяет вершины одного
множества от другого. Итак, вершины
отделяются всеми разрезами, соответствующими
дугам
множества вершин двух компонент связности
графа T-u.
Этот разрез отделяет вершины одного
множества от другого. Итак, вершины
отделяются всеми разрезами, соответствующими
дугам
![]() .
Т.е. справедливо:
.
Т.е. справедливо:
![]() .
(7)
.
(7)
Обратно.
Покажем, что если на любом шаге
построения узлы
![]() соединяет
в дереве ребро пропускной способ-
соединяет
в дереве ребро пропускной способ-
ности
v,
то существуют такие вершины
![]() ,
что v(i,j)=v.
На первом шаге это, конечно, верно.
Докажем, что это свойство сохраняется
и дальше.
,
что v(i,j)=v.
На первом шаге это, конечно, верно.
Докажем, что это свойство сохраняется
и дальше.
|
Пусть
на некоторой итерации будет разбито
.
Перед разбиением, по индукционному
предположению существуют вершины
,
что v(i,j)=v.
Пусть
|
Тогда
множество
разобьется на
![]() ,
где
,
где
![]()
|
Если
j![]() ,
то двумя искомыми узлами будут i,
j
и v(i,j)=v
. Если j
,
то двумя искомыми узлами будут i,
j
и v(i,j)=v
. Если j![]() ,
то рассмотрим вершины i,s.
Эти вершины находятся по одну сторону
от минимального (s,t)-разреза
пропускной способности v’.Следовательно,
сжатие множества
не
влияет на v(s,i).
Вместо сжатия можно все пропускные
способности в
приравнять ∞. Имеем в такой сети новые
величины максимальных потоков:
,
то рассмотрим вершины i,s.
Эти вершины находятся по одну сторону
от минимального (s,t)-разреза
пропускной способности v’.Следовательно,
сжатие множества
не
влияет на v(s,i).
Вместо сжатия можно все пропускные
способности в
приравнять ∞. Имеем в такой сети новые
величины максимальных потоков:
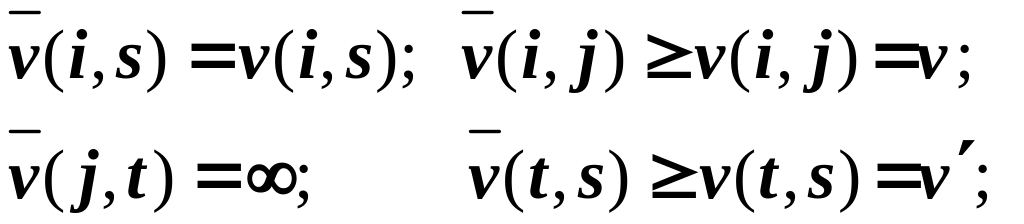
Из (2) имеем
![]()
Но
![]() ,
т.к. v
минимальная пропускная способность
(i,j)-разреза
. Поэтому
,
т.к. v
минимальная пропускная способность
(i,j)-разреза
. Поэтому
![]() .
Так как i
и s
отделяет разрез пропускной способности
v,
то
.
Так как i
и s
отделяет разрез пропускной способности
v,
то
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Таким образом, пропускные способности дуг в последнем дереве Т фактически представляют величины
максимальных потоков между смежными узлами дерева Т. Из (3) следует, что
(8)
для
любого подмножества вершин
, соединяющего
![]() в последнем дереве. Это вместе с (7)
устанавливает лемму и доказывает, что
наше построение приводит к эквивалентному
дереву.
в последнем дереве. Это вместе с (7)
устанавливает лемму и доказывает, что
наше построение приводит к эквивалентному
дереву.
ПРИМЕР ЗАДАЧИ О МНОГОПОЛЮСНОМ МАКСИМАЛЬНОМ ПОТОКЕ
Рассмотрим сеть, изображенную на рис. 2.57. Числа, приписанные дугам, соответствуют их пропускным способностям. Требуется для каждой пары вершин сети определить величину максимального потока между ними.
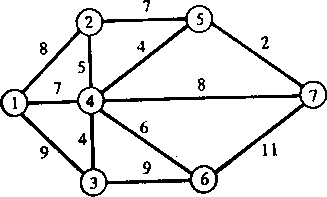
Рис. 2.57. Сеть в задаче о многополюсном максимальном потоке.
Данная задача решается за 6 итераций алгоритма Гомори—Ху. Если процедура расстановки пометок применялась бы к каждой паре узлов, то потребовалось бы решить 21 задачу о максимальном потоке.
Итерация 1. Рассмотрим узлы s = 2 и t = 5. Величина максимального потока равна 13. Поэтому v(2,5)=v(5,2)= 13. По разрезу с минимальной пропускной способностью мы определяем, что построение дерева разрезов можно начать с ветви, соединяющей узел 5 и конденсированный узел, состоящий из вершин 1, 2, 3 4, 6, 7 (рис. 2.58а). Вес данной ветви равен 13.
Итерация 2. Рассмотрим узлы s=l и t = 2. Величина максимального потока равна 19. Поэтому v12 = v21 =19. По минимальному разрезу мы определяем, что узлы 2 и 5 лежат по одну его сторону, а все остальные узлы сети — по другую сторону этого разреза (рис. 2.586). Вес ветви, соединяющей узел 2 и конденсированный узел, состоящий из вершин 1, 3, 4, 6 и 7, равен 13.
1,2,3,4,6,7
5
13




{
. Рис. 2.58а. Задача о максимальном потоке: первая итерация.
5
2
13
19
1,3,4,6,7


Рис 2.586. Вторая итерация.
Итерация 3. Рассмотрим узлы 6 и 7. Величина максимального потока равна 21. Поэтому v67 = v76 = 21. По минимальному разрезу мы определяем, что узел 7 в дереве разрезов соединяется с конденсированным узлом, состоящим из вершин 1, 3, 4, 6, ребром, вес которого равен 21. Кроме того, узлы 2 и 5 и конденсированный узел (1, 3, 4, 6) расположены по одну сторону мини мального разреза, а узел 7 — по другую сторону этого разреза (рис. 2.58в).
Итерация 4. Рассмотрим узлы s = 4 и t = 6. Величина максимального потока равна 25. Поэтому v46 = v64 = 25. По минимальному разрезу видно, что узлы 6 и 7 расположены в той же части дерева разрезов, что и узел (1, 3, 4) (рис. 2.58г).
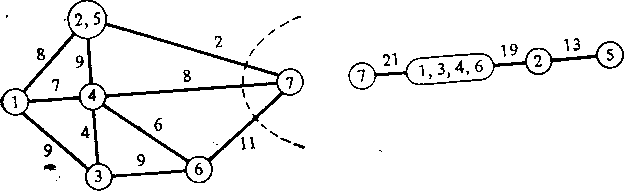
Рис. 2.58в. Третья итерация.
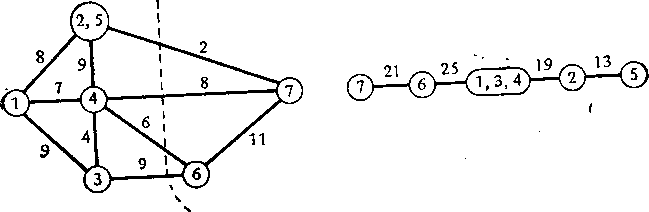
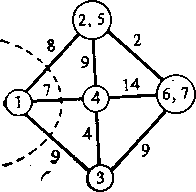
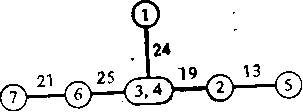
Рис. 2.58Д. Пятая итерация
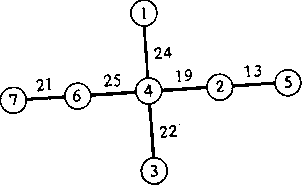
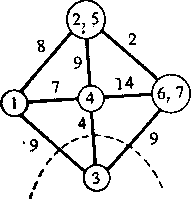
Рис. 2.58е. Шестая итерация.
Итерация 5. Рассмотрим узлы 5=1 и / = 4. Величина максимального потока равна 24. Поэтому 1;14 = а41=24. Определяя минимальный разрез, удаляем узел 1 из узла (1, 3, 4) и располагаем его по ту сторону узла (3, 4), где не находится ни один из оставшихся вершин (рис. 2.58д). Вес соответствующей дуги в дереве разрезов равен 24.
Итерация 6. Рассмотрим узлы s = 3 и /=4. Величина максимального потока равна 22. Поэтому Уз4 = ^4з = 22. Найдя минимальный разрез, удаляем узел 3 из узла (3, 4) и соединяем его с узлом 4 дугой дерева разрезов, вес которой равен 22. Теперь дерево разрезов стало полным, т. е. состоит из шести дуг. Поэтому процедура заканчивается (рис. 2.58е).