- •Формальное описание алгоритма 1 задачи “Ближайшая пара”
- •Лекция 2 Задача о битоническом пути
- •Битонический путь
- •Лекция 3 Динамическое программирование и оптимизационная задача перемножения матриц.
- •2. Алгоритмизация описанного процесса на основе (2) и (3).
- •Лекция 4 Оптимальная триангуляция треугольника.
- •Лекция 5
- •Циркуляция.
- •Лекция 6 Многополюсные максимальные потоки
- •Алгоритм гомори—ху
- •Лекция 7 Задача распределения капитала
- •1. Случай запрета коротких позиций.
- •2. Случай разрешения коротких позиций.
- •Случай наличия безрискового актива.
- •Лекция 8 Потоковые алгоритмы.
- •Лекция 9. Алгоритм Гомори.
- •Лекция 10 Многополюсные минимальные потоки.
- •Лекция 11 доминирующие множества и абсолютный центр.
- •Доминирующие множества.
- •Нахождение абсолютного p-центра
- •Ленкция 12 простой (классический) генетический алгоритм.
- •Лекция 13 Стохастическая задача размещения-распределения объектов.
Конспект лекций по спецкурсу «Дополнительные главы исследования операций»
Лекции – 30 час
Лаб работы - 30. час
Лекция 1
Задача “Ближайшая пара”
Пусть даны N точек n-мерного пространства:
![]()
Задача о ближайшей паре состоит в поиске двух точек среди данных, находящихся на минимальном расстоянии друг от друга.
Сформулированную задачу можно решить с помощью следующих алгоритмов:
Алгоритм 1. (”Разделяй и властвуй”)
Данный алгоритм является рекурсивным, он базируется на следующих правилах:
Правило 0.
Разбить множество на два непустых подмножества методом деления пополам (при этом точки должны быть упорядочены по первой координате).
Правило 1.
Если множество состоит не более, чем из 3-х точек, то перебрав все пары точек, найти минимальное расстояние между двумя точками.
Правило 2.
Найти минимальное расстояние d множества V{ } следующим образом:
Пусть
множество точек V
= {![]() }
содержит более 3-х точек. Разбить его на
два
}
содержит более 3-х точек. Разбить его на
два
![]() (см. Правило 0). Вычислить рекурсивно
минимальное расстояние для обоих
подмножеств соответственно dVL
и dVR.
Положить d
= min(dVL,
dVR).
Затем среди пар точек PVL
и RVR
найти две ближайшие, определив расстояние
d1.
Положить d
= min(d,
d1).
(см. Правило 0). Вычислить рекурсивно
минимальное расстояние для обоих
подмножеств соответственно dVL
и dVR.
Положить d
= min(dVL,
dVR).
Затем среди пар точек PVL
и RVR
найти две ближайшие, определив расстояние
d1.
Положить d
= min(d,
d1).
Алгоритм 2. (”В лоб”)
Вычислить расстояние между любыми двумя точками, а затем найти минимальное путем сравнения.
Формальное описание алгоритма 1 задачи “Ближайшая пара”
Вход: n – число точек
x [1..n, 1..2] – координаты этих точек (упорядоченных по первой
координате)
Выход:
d – расстояние между ближайшей парой
![]() их
порядковые номера
их
порядковые номера
PRCD(x)
 num
(массив номеров вершин, упорядоченных
по второй координате)
num
(массив номеров вершин, упорядоченных
по второй координате)PAIR(1, n,
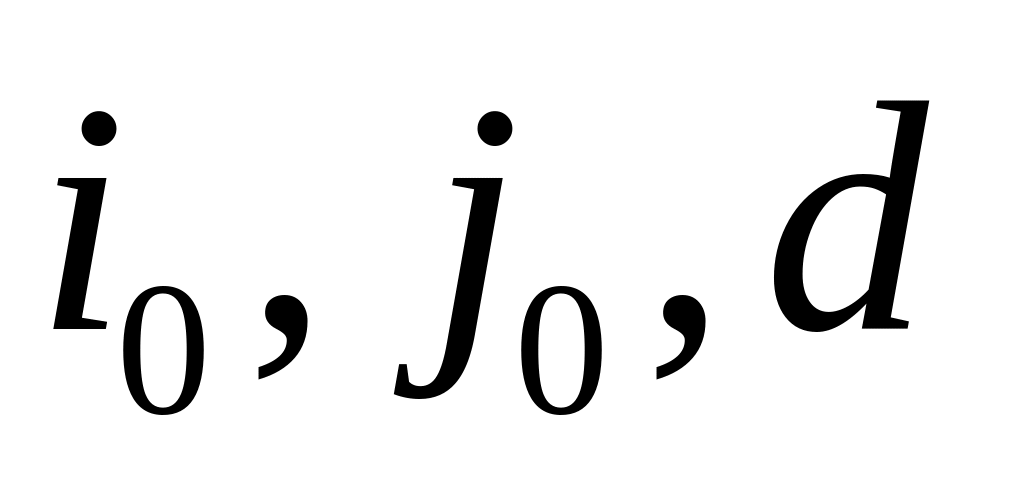 )
–
определяет ближайшую пару
)
–
определяет ближайшую пару
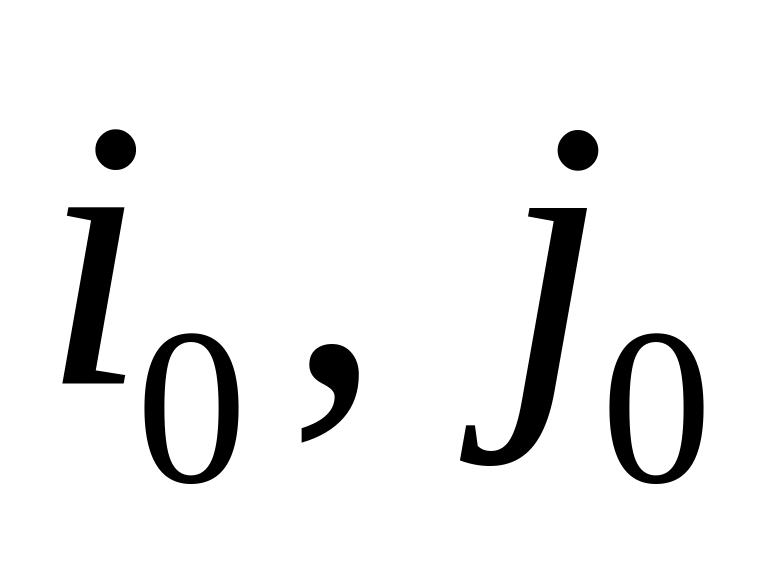
PAIR( k, l, )
– ищет ближайшую пару на множестве точек, начиная с k – ой и кончая l – ой
if
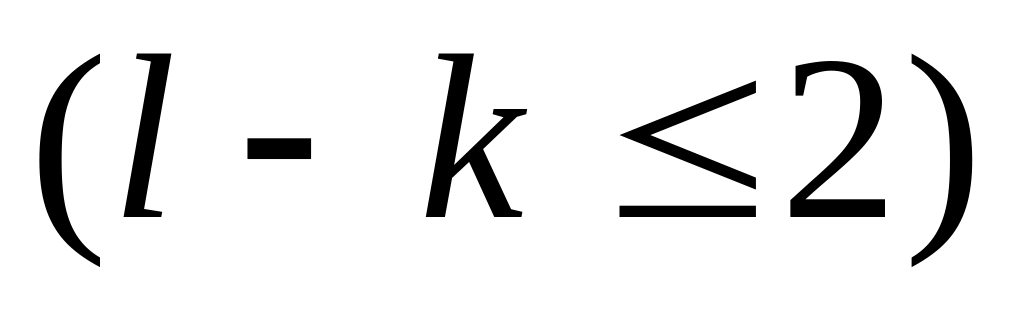 then
then
for i:=k to ( l – 1) do
for j:=i+1 to l do
if
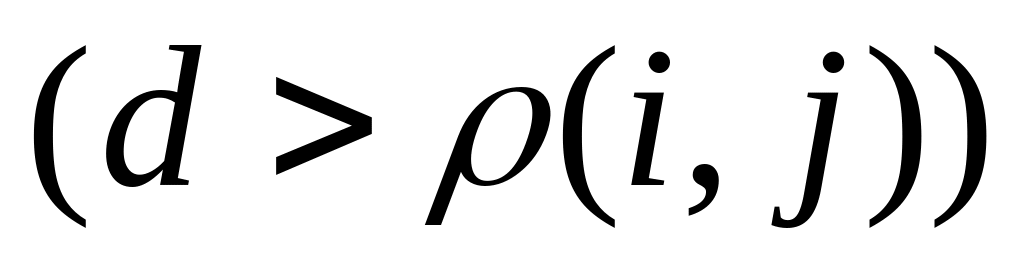 then
then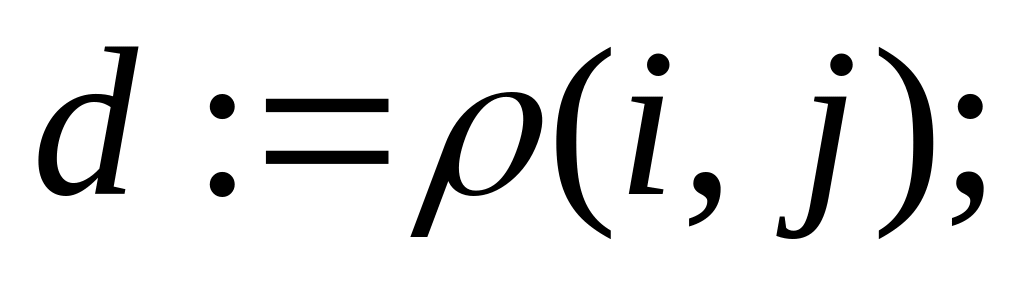

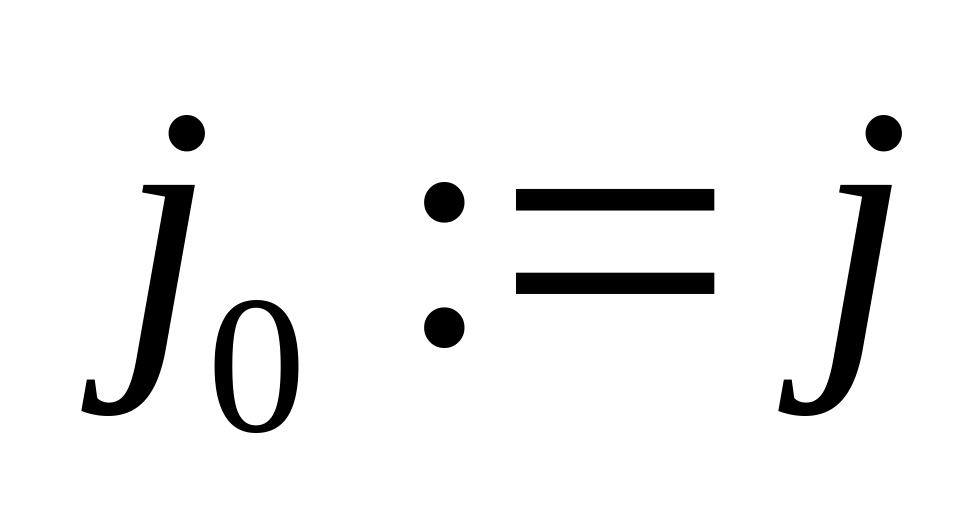
else PAIR( k,
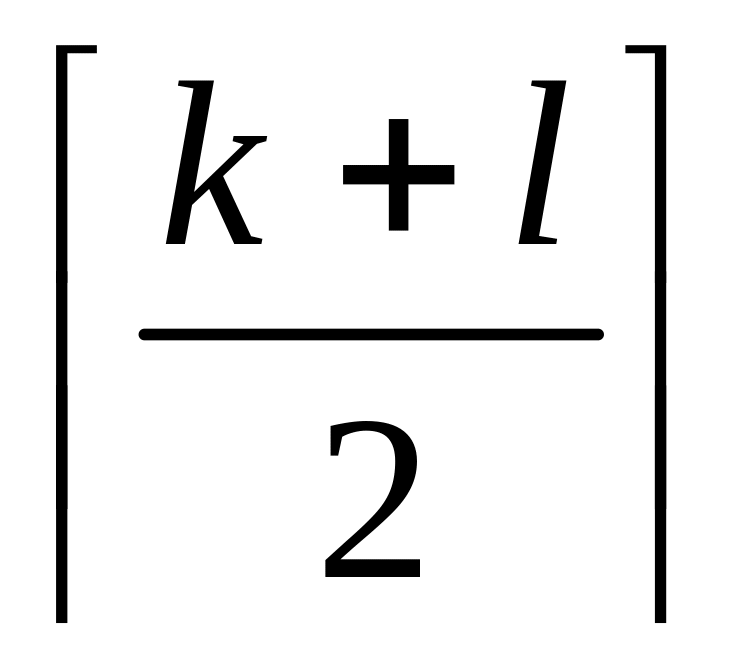 ,
,
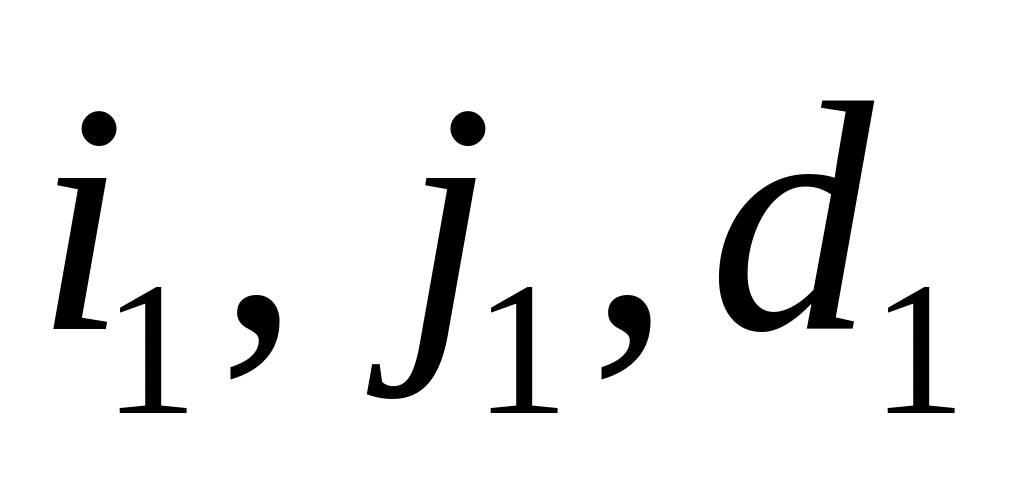 )
)PAIR(
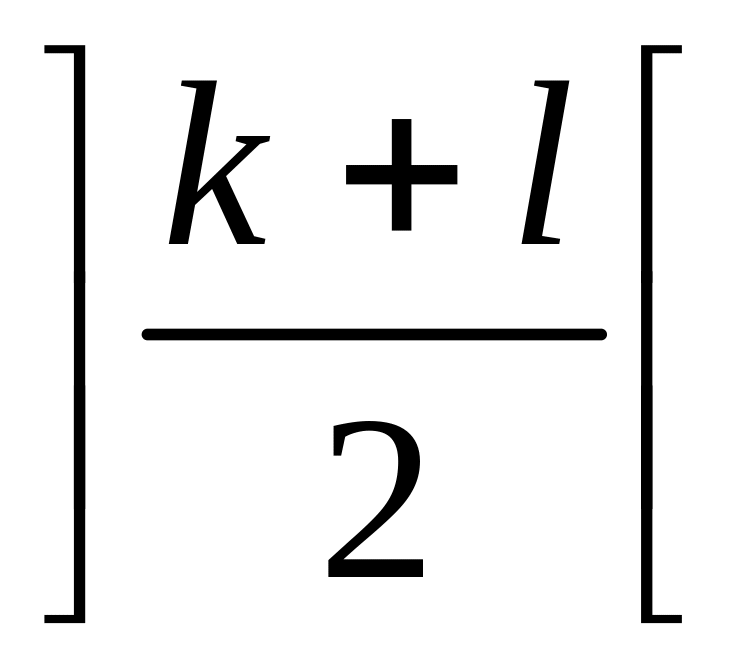 ,
l,
,
l,
 )
)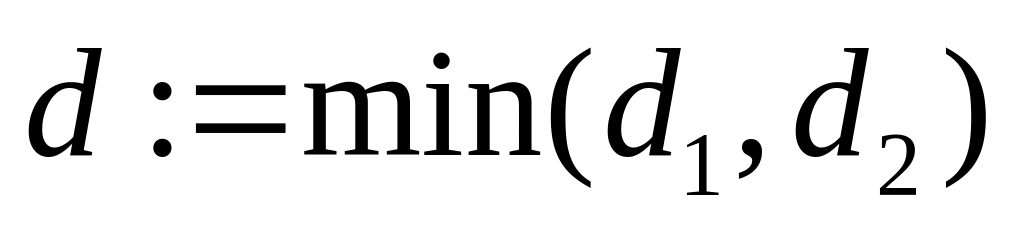
if
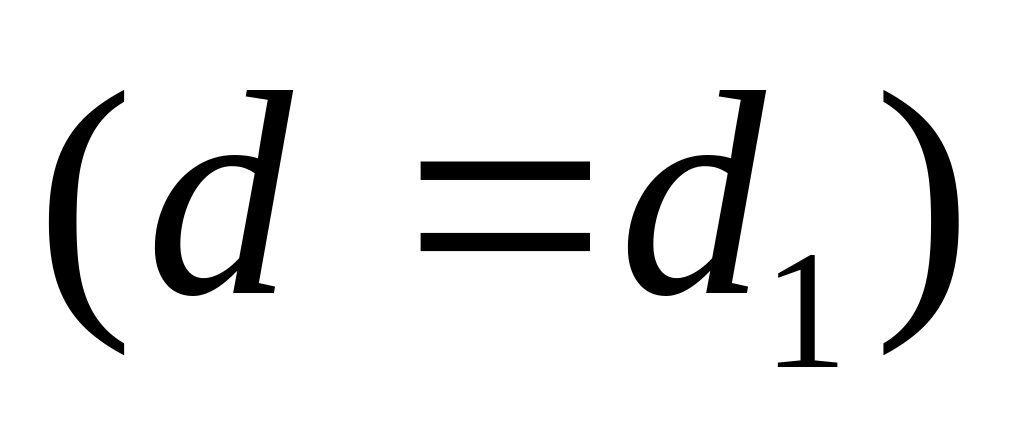 then
then
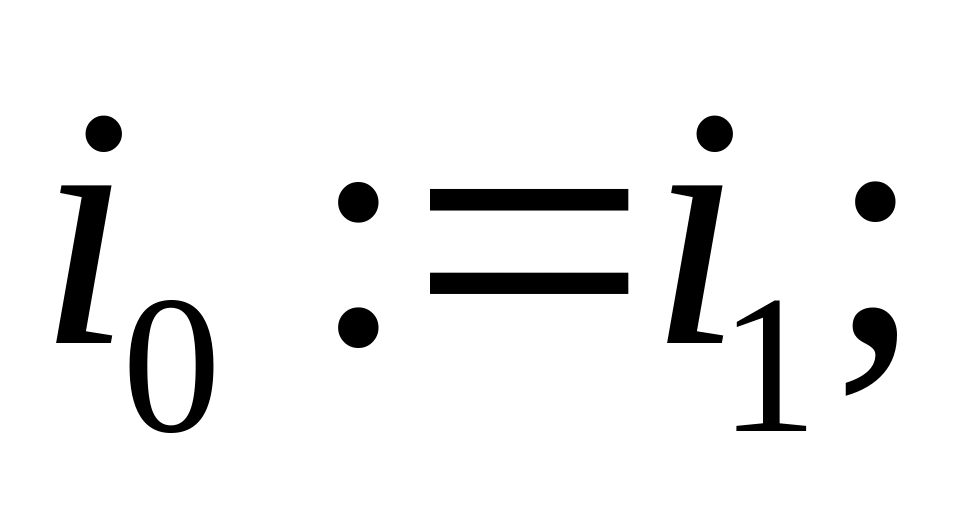
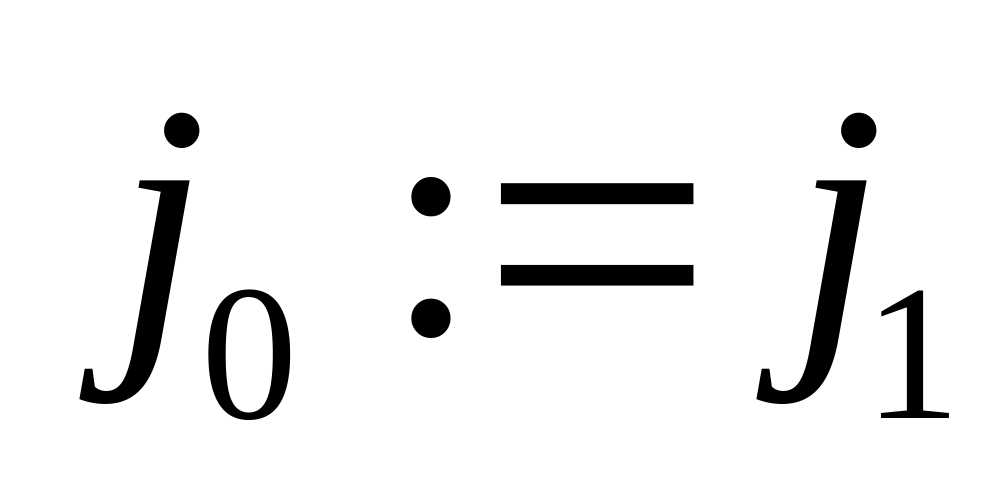
else
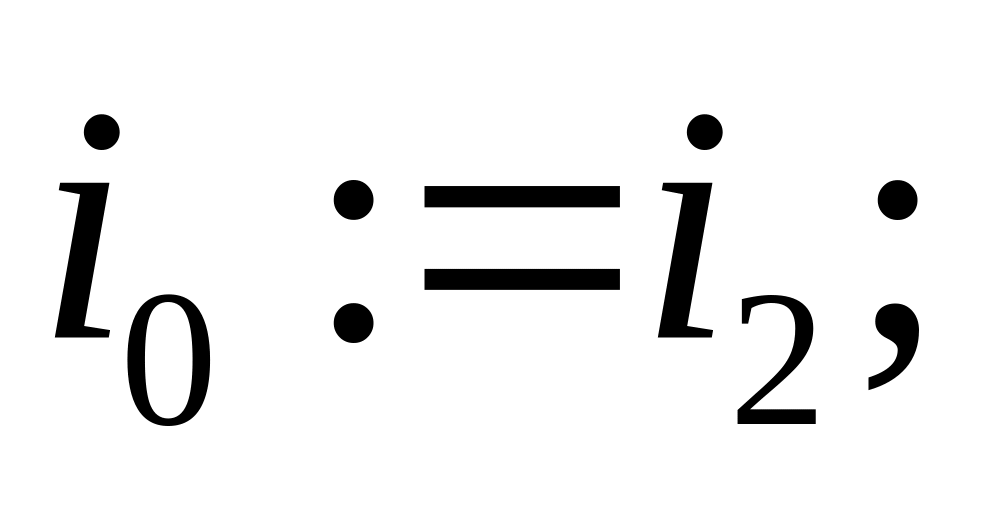
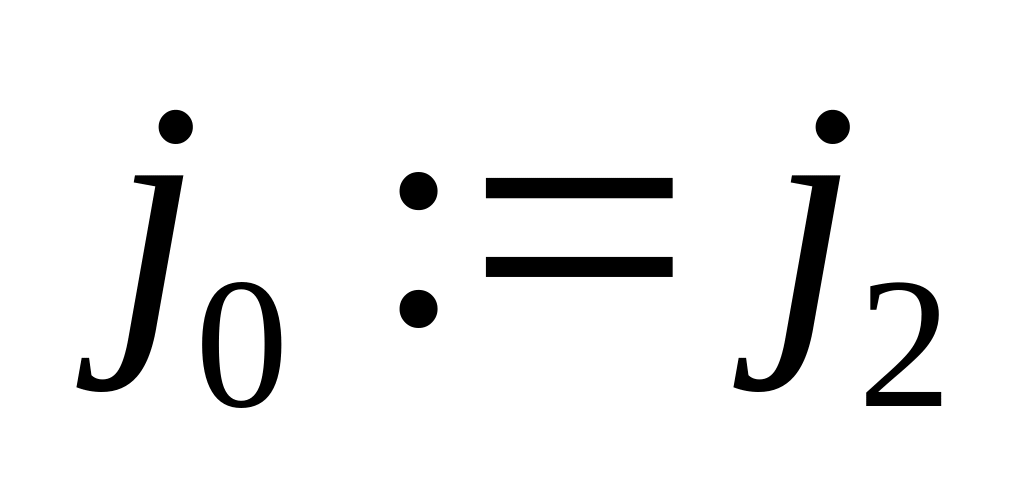
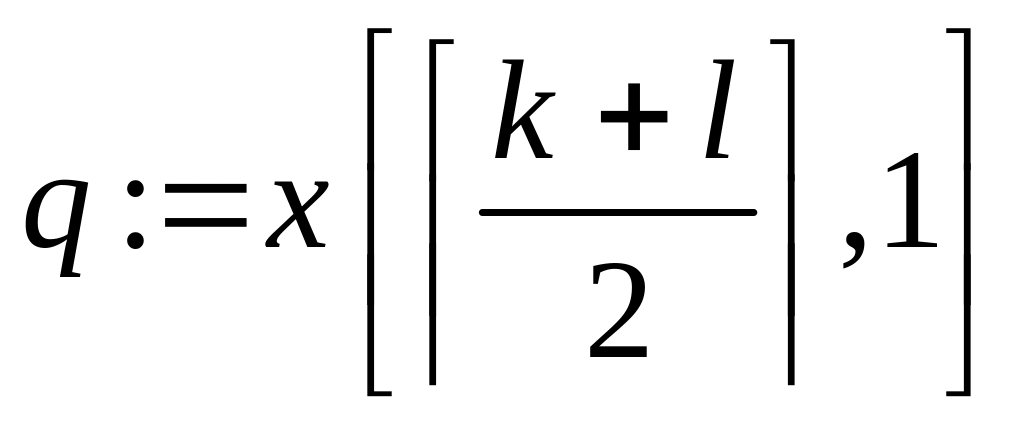
for i:=k to do
if ( x [ i, 1] > q – d ) then
for j:=1 to n do
if
 &
&
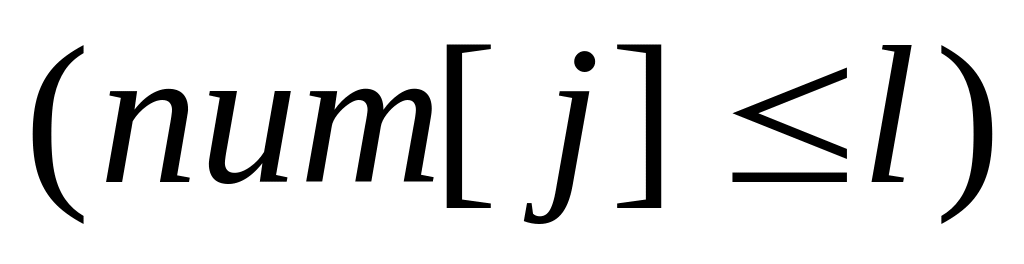
&
![]() &
&
![]()
then

if
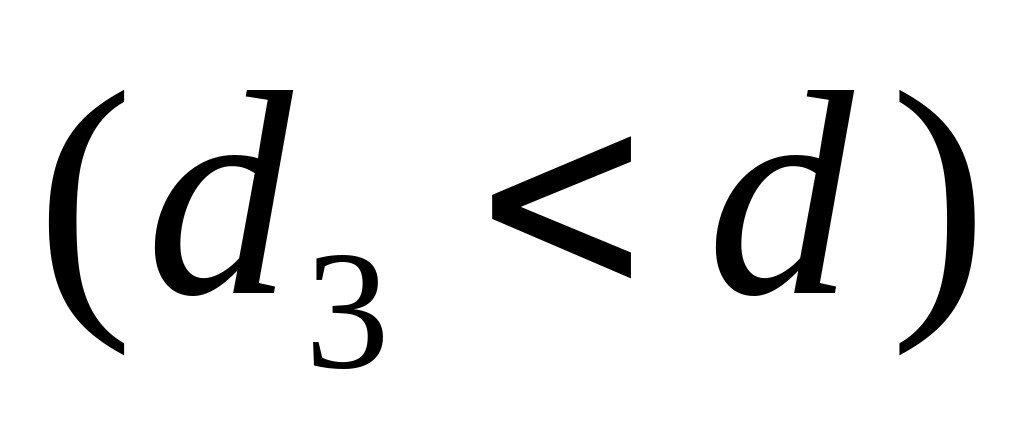 then
then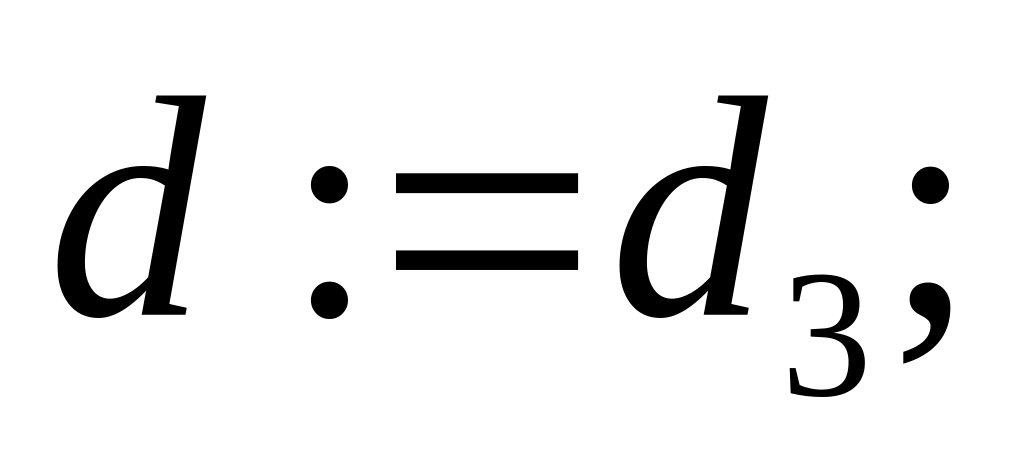
![]()
Лекция 2 Задача о битоническом пути
Пусть
на плоскости даны ![]() точек, упорядоченных по оси
точек, упорядоченных по оси ![]()
![]()

![]()
Задача:
обойти эти точки, начиная с ![]() по одному разу так, чтобы вернуться в
(через одну точку пройти один раз) и
чтобы суммарная длина пути была
минимальной.
по одному разу так, чтобы вернуться в
(через одну точку пройти один раз) и
чтобы суммарная длина пути была
минимальной.
Данная задача – это частный случай задачи о гамильтоновом контуре.
Нам необходимо найти путь минимальной суммарной длины.
![]()
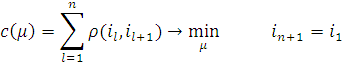
Данная задача решается методом динамического программирования.
Рассмотрим
часть пути на множестве вершин ![]()
Путь,
имеющий самую малую длину обозначим
![]()
|
|
|
… |
j |
1 |
|
|
|
|
|
… |
|
|
i |
Возможны случаи:
Следовательно,
часть пути ![]() ,
соединенного с
,
соединенного с ![]() и
и ![]() также будет кратчайшим.
также будет кратчайшим.
Следовательно,
![]()
Следовательно, соединяем точки 1 и 2
Теорема
О структуре оптимального решения
Пусть
![]() - оптимальный путь на множестве вершин
- оптимальный путь на множестве вершин
![]() и пусть
- предпоследняя вершина, предшествующая
и пусть
- предпоследняя вершина, предшествующая
![]() ,
тогда
,
тогда
если , следовательно
если
,
следовательно ![]()
При этом часть пути также является оптимальным.
Доказательство:
Длина кратчайшего пути:
![]()
Если
одна из частей хотя бы оного из слагаемых
не оптимальна, то это противоречит тому,
что ![]() оптимально.
оптимально.
Обозначим
через ![]() длину оптимального пути
длину оптимального пути
Р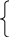 екуррентная
формула длины оптимального пути для
екуррентная
формула длины оптимального пути для
![]() :
:
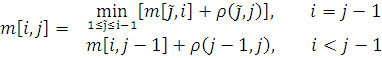
![]()
![]()
Пример
Даны точки:
(1,7), (2,1), (3,4), (6,5), (7,2), (8,6), (9,3)
|
2 |
3 |
4 |
5 |
6 |
7 |
1 |
6,08 1 |
9,25 2 |
12,4 3 |
15,57 4 |
19,7 5 |
22,9 6 |
2 |
|
9,7 1 |
12,9 3 |
16 4 |
20,1 5 |
23,3 6 |
3 |
|
14,6 1 |
17,8 4 |
21,9 5 |
25,1 6 |
|
4 |
|
17,9 2 |
22,1 5 |
25,2 6 |
||
5 |
|
20,12 4 |
23,3 6 |
|||
6 |
|
22,4 5 |
||||
Сделаем несколько расчетов
![]()
![]()
![]()
![]()
![]()
![]()
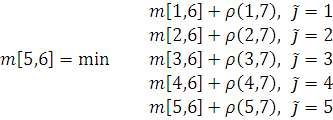
![]()
OPT
= ![]()
S[i,j] – номер предпоследней вершины, предшествующей j, i<j
Построим битонический путь:
1 |
3 |
4 |
6 |
|
|
|
|
|
7 |
|
|
2 |
5 |
|
Запишем схему сверху-вниз:
Вход: n, x[1..n], y[1..n]
Выход: S, OPT
for i:=1 to n-1 do
for j:=i+1 to n do
if i=j-1
then if i=1
then m[i,j]:=
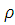 (i,j)
(i,j)S[i,j]:=i
else m[i,j]:=∞
for k:=1 to i-1 do
d:=m[k,i]+ (k,j)
if d<m[i,j]
then m[i,j]:=d
S[i,j]:=k
else m[i,j]:=m[i,j-1]+ (j-1,j)
S[i,j]:=j-1
OPT:=m[n-1,n]+ (n-1,n)
Процедура выдачи на печать оптимального битонического пути:
Вход: n, S[1..n,1..n]
Выход: на печать
st:=” ”, st1:=” ”
RPP(n,n)
Печать (st, n, st1)
RPP(i,j)
If i=1 или j=1
Then Return
If i=n и j=n
Then st1:=str(n-1)+st1
RPP(n-1,n)
If i<j
Then st:=str(S[i,j]+st)
RPP(i,S[i,j])
If i>j
Then st1:= str(st1+S[j,i])
RPP(S[j,i],j)
Return “ “